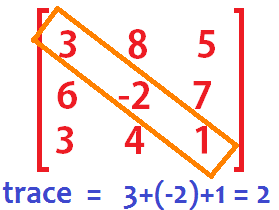Matrices | Engineering Mathematics - Civil Engineering (CE) PDF Download
Introduction
- A matrix represents a collection of numbers arranged in an order of rows and columns. It is necessary to enclose the elements of a matrix in parentheses or brackets.

A matrix with 9 elements is shown below:
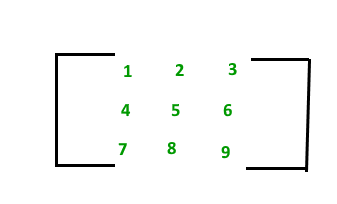 This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number.
This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number.
Example: a23 = 6
➢ Order of a Matrix
- The order of a matrix is defined in terms of its number of rows and columns.
Order of a matrix = No. of rows ×No. of columns - Therefore Matrix [M] is a matrix of order 3 × 3.
➢ Transpose of a Matrix
- The transpose [M]T of an m x n matrix [M] is the n x m matrix obtained by interchanging the rows and columns of [M].
- If A= [aij] mxn , then AT = [bij] nxm where bij = aji
➢ Properties of Transpose of a Matrix
- (AT)TT = A
- (A+B)TT = ATT + BTT
- (AB)TT = BTTATT
➢ Singular and Nonsingular Matrix
- Singular Matrix: A square matrix is said to be singular matrix if its determinant is zero i.e. |A|=0.
- Nonsingular Matrix: A square matrix is said to be non-singular matrix if its determinant is non-zero.
➢ Properties of Matrix Addition and Multiplication
- A+B = B+A (Commutative)
- (A+B)+C = A+(B+C) (Associative)
- AB ≠ BA (Not Commutative)
- (AB) C = A (BC) (Associative)
- A (B+C) = AB+AC (Distributive)
➢ Square Matrix
- A square Matrix has as many rows as it has columns. i.e. no of rows = no of columns.
➢ Symmetric Matrix
- A square matrix is said to be symmetric if the transpose of original matrix is equal to its original matrix. i.e. (AT) = A.
➢ Diagonal Matrix
- A Symmetric matrix is said to be diagonal matrix where all the off diagonal elements are 0.
➢ Identity Matrix
- A diagonal matrix with 1s and only 1s on the diagonal. Identity matrix is denoted as I.
➢ Orthogonal Matrix
- A matrix is said to be orthogonal if AAT = ATA = I
➢ Idempotent Matrix
- A matrix is said to be idempotent if A2 = A
➢ Involutory Matrix: A matrix is said to be Involutory if A2 = I.
Note: Every Square Matrix can uniquely be expressed as the sum of a symmetrix matrix and skew symmetric matrix. A = 1/2 (AT + A) + 1/2 (A – AT).
➢ Adjoint of a Square Matrix
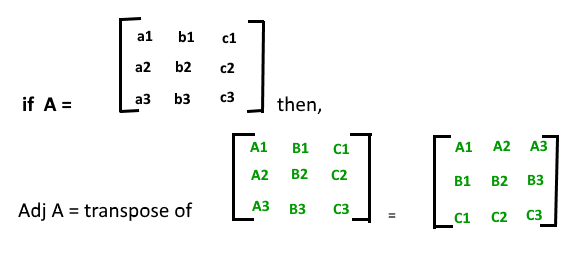
➢ Properties of Adjoint
- A(Adj A) = (Adj A) A = |A| In
- Adj(AB) = (Adj B).(Adj A)
➢ Inverse of a Square Matrix
- A-1 = Adj A / |A| ; |A|#0
➢ Properties of Inverse
- (A-1)-1 = A
- (AB)-1 = B-1A-1
- Only a non-singular square matrix can have an inverse.
➢ Where should we use Inverse Matrix?
- If you have a set of simultaneous equations:
► 7x + 2y + z = 21
► 3y – z = 5
► -3x + 4y – 2x = -1 - As we know when AX = B, then X = A-1B so we calculate the inverse of A and by multiplying it B, we can get the values of x, y and z.
➢ Trace of a Matrix
- Trace of a matrix is denoted as tr(A) which is used only for square matrix and equals the sum of the diagonal elements of the matrix.
Example:
|
65 videos|122 docs|94 tests
|
FAQs on Matrices - Engineering Mathematics - Civil Engineering (CE)
| 1. What are matrices in computer science engineering? |  |
| 2. What are some common operations performed on matrices in computer science engineering? |  |
| 3. How are matrices used in computer graphics? |  |
| 4. What is the importance of matrices in machine learning? |  |
| 5. How are matrices used in scientific computing? |  |