Polynomials, Polynomials in One Variable and Degree of a Polynomials - Class 9, Mathematics PDF Download
"The word polynomial means an algebraic expression consisting of one or many terms involving powers of the variable. Poly means many or much.
INTRODUCTION
In our earlier classes, we have studied about algebraic expressions, their addition, subtraction and multiplication etc. We have also studied about factorisation using some formulae. We have also learnt the formulae.
and their use in factorisation. In this chapter we shall study about particular types of algebraic expressions, called polynomials. We shall also study the remainder and factor theorems and shall use them in factorisation of polynomials. We shall also discuss some more algebraic indentities and their use in factorisation.
HISTORICAL FACTS
Determining the roots of polynomials, or "solving algebraic equations", is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations were written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine Sections, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou". We would write 3x + 2y + z = 29.
Rene Descartes The earliest known use of the equal sign is in Robert Recorde's The Whetstone of Witte, 1557. The signs + for addition, – for subtraction, and the use of a letter for an unknown appear in Michael Stifel's Arithmetica Integra, 1544. Rene Descartes, in La geometrie, 1637, introduced the concept of the graph of a polynomial equation. He popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen in the general formula for a polynomial, where the a's denote constants and x denotes a variable. Descartes introduced the use of superscripts to denote exponents as well.
CONSTANT AND A VARIABLE
In algebra, two types of symbols are used : constants and variables (literals)
(i) Constant : A symbol whose value remains same throughout a particular problem is called constant.
(ii) Variable : A symbol whose value changes according to the situation is called variable or literal. It is denoted by the letters of alphabet a, b, c ....... x, y, z, etc.
Ex. : 3x + 5y, 7y – 2x, 2x – ay + az etc.
ALGEBRAIC EXPRESSIONS
A combination of constants and variables connected by any fundamental operation (i.e. +, –, × and ÷) is called an algebraic expression.
Ex. : 3x + 5y, 7y – 2x, 2x – ay + az etc.
TERM OF AN EXPRESSION
A constant, a variable or a combination of a constant and variable connected with the operation of multiplication or division is called a term.
|
Algebraic expression |
Number of terms |
Terms |
|
– 25x |
1 |
– 25x |
|
2x + 3y |
2 |
2x and 3y |
|
4x2 – 3xy + 5z |
3 |
4x2, – 3xy, 5z |
|
|
4 |
|
Factors of term :
The algebraic expression 4x2 + 5xy2 consists of two terms 4x2 and 5xy2. The term 4x2 is the product of 4, x and x and the factors of the term 5xy2 are 5, x, y and y.
So, we can express the factors of 4x2 + 5xy2 in terms of tree diagram as follows :-
COEFFICIENTS Any factor of a term is called the coefficient of the remaining term.
For example :- (i) In 7x ; 7 is coefficient of x
(ii) In – 5x2y ; 5 is coefficient of –x2y ; –5 is coefficient of x2y,
Ex. Write the coefficient of :
(i) x2 in 3x3 – 5x2 + 7
(ii) xy in 8 xyz
(iii) –y in 2y2 – 6y + 2
(iv) x0 in 3x + 7
Sol. (i) –5
(ii) 8z
(iii) 6
(iv) Since x0 = 1, Therefore 3x + 7 = 3x + 7x0 ⇒ coefficient of x0 is 7.
1. POLYNOMIALS
An algebraic expression of the form p(x) = anxn + an–1xn–1 + an–2xn–2 +............+ a1x1 + a0x0
where an ≠ 0 and a0, a1, a2,.......an are real numbers and each power of x is a positive integer, is called a polynomial.
Hence, an, an–1, an–2, are coefficients of xn, xn–1 ..............x0 and anxn, an–1xn–1, an–2xn–2,............ are terms of the polynomial. Here the term anxn is called the leading term and its coefficient an, the leading coefficient.
For example : is a polynomial in variable u.
are known as terms of polynomial and
are their respective coefficients.
TYPES OF POLYNOMIALS Generally we divide the polynomials into three categories.
Polynomials classified by number of distinct variables
| Number of dis tinct variables |
Name |
Example |
| 1 | Univariate | x + 9 |
| 2 | Bivariate | x + y + 9 |
| 3 | Trivariate | x + y + z + 9 |
Generally, a polynomial in more than one variable is called a multivariate polynomial.
A second major way of classifying polynomials is by their degree. Recall that the degree of a term is the sum of the exponents on variables, and that the degree of a polynomial is the largest degree of any one term.
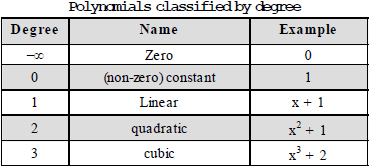
Usually, a polynomial of degree n, for n greater than 3, is called a polynomial of degree n, although the phrases quartic polynomial and quintic polynomial are sometimes used.
The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather the degree of the zero polynomial is either left explicitly undefined, or defined to be negative (either –1 or – ∞)
Polynomials classified by number of non-zero terms
| Number of non-zero terms | Name | Example |
| 0 | zero polynomial | 0 |
| 1 | monomial | x2 |
| 2 | binomial | x2 + 1 |
| 3 | trinomial | x2 + x + 1 |
If a polynomial has only one variable, then the terms are usually written either from highest degree to lowest degree ("descending powers") or from lowest degree to highest degree ("ascending powers").
3. VALUE OF A POLYNOMIAL
Let f(x) be a polynomial in variable x and α is any real number, then the value of polynomial at x = α is obtained by substituting x = α in the value of polynomial and is denoted by f(α ).
Ex. : Consider a polynomial f(x) = 3x2 – 4x + 2, find the value at x = 3. replace x by 3 everywhere
So, the value of
f(x) = 3x2 – 4x + 2 at x = 3 is
f(3) = 3 × (3)2 – 4 × 3 + 2 = 27 – 12 + 2 = 17
Similarly the value of polynomial f(x) = 3x2 – 4x + 2
at x = –2 is f(–2) = 3(–2)2 – 4 × (–2) + 2 = 12 + 8 + 2 = 22
at x = 0 is f(0) = 3(0)2 – 4 (0) + 2 = 0 – 0 + 2 = 2
at is
FAQs on Polynomials, Polynomials in One Variable and Degree of a Polynomials - Class 9, Mathematics
| 1. What are polynomials? |  |
| 2. What are polynomials in one variable? |  |
| 3. How do you determine the degree of a polynomial? |  |
| 4. Can a polynomial have a negative degree? |  |
| 5. How are polynomials used in real-life applications? |  |















