Simplification | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| Simplification |

|
| Tips and tricks to solve simplification and approximation questions |

|
| Important formulas for solving Problems In Arithmetic |

|
| Edurev Tip |

|
Simplification
The Simplification topic focuses on simplifying mathematical expressions, including arithmetic, fractions, algebraic expressions, square/cube roots, and exponents. It involves applying the BODMAS rule, simplifying fractions, combining like terms in algebraic expressions, and handling powers. The goal is to solve problems quickly and accurately by breaking them down into simpler steps. Practicing without a calculator helps improve speed and accuracy.
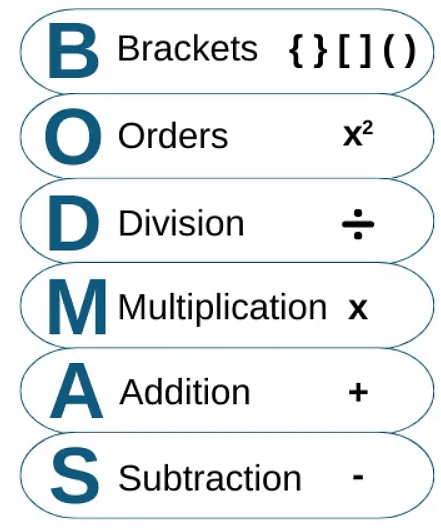
BODMAS Rule
The BODMAS rule is a guideline used to solve mathematical expressions in the correct order. According to this rule, operations within brackets are performed first, followed by exponents, division and multiplication (from left to right), and lastly, addition and subtraction (from left to right). This ensures that mathematical expressions are solved in the correct sequence.
For instance, 20 – 15 + 2 – 4 means that 15 is to be subtracted from 20 then 2 is to be added to the result and then 4 is to be subtracted from the result.
Brackets
The expressions within brackets are to be treated as a single identity thus 6 x (3 – 2) means that 6 is to be multiplied by the difference of 3 and 2. So 6 x (3 – 2) = 6 x 1 = 6
Note: Operations within the bracket are to be carried first.
Brackets are of 4 types.
- Bar bracket or Vinculum
- Circular bracket ( )
- Curly bracket { }
- Square bracket [ ]
Removal of a bracket
5 + (9 + 2) is equal to 5 + 11 = 16
5 + (9 – 2) is equal to 5 + 7 = 12
The rule is that when a bracket is preceded by a + sign, the bracket may be removed without making any change in the expression.
Now consider the expressions when the bracket is preceded by a ‘–’ sign
20 – (8 + 3) = 20 – 11 = 9 also 20 – (8 + 3) = 20 – 8 – 3 = 9
20 – (8 – 3) = 20 – 5 = 15 also 20 – (8 – 3) = 20 – 8 + 3 = 12 + 3 = 15
The rule is that if a bracket is preceded by a negative (–) sign, the bracket can be removed by changing the sign of every term within the bracket.
Bracket within a bracket
Let us take an example. Supposing we want to simplify
We will first remove the bar bracket then circular bracket, then curly bracket and at the last stage, we remove the square bracket.
So the expression given above is
= 24 – [12 – {8 – (9 – 2 – 3)}]
= 24 – [12 – {8 – 4}]
= 24 – [12 – 4]
= 24 – 8
= 16
The rule of VBODMAS gives us the arrangement according to which an expression is to be simplified. VBODMAS stands for vinculum, brackets, of, division, multiplication, addition and subtraction respectively.
Tips and tricks to solve simplification and approximation questions
- When fractions share a common denominator, calculate the integer and fractional parts separately.
- To approximate an expression with decimals, convert the decimals into integers and solve the problem.
- For decimal numbers, round them off to the nearest whole number. For instance, treat 46.72 as 47 or 21.10 as 21.
- Always apply the BODMAS rule when solving approximation or simplification problems.
- Memorizing multiplication tables up to 20 can save valuable time, especially for complex questions.
- Avoid overcomplicating the problems; skip hard calculations to solve the equations as quickly as possible.
- Keep important formulas in mind that can be applied to such questions.
Important formulas for solving Problems In Arithmetic
- (a+b) (a-b) = a2 - b2
- (a+b)2 = a2 + b2 + 2ab
- (a – b) 2 = a2 + b2 – 2ab
- (a + b)3 = a3 + b3 + 3ab (a+b)
- (a – b)3 = a3 – b3 – 3ab (a–b)
- a2 + b2 = (a + b)2 – 2ab
- a3 + b3 = (a+b) (a2 + b2 – ab) = (a+b)3 – 3ab (a+b)
- a3 - b3 = (a – b) ( a2 + b2 + ab) = (a–b)3 + 3ab (a-b)
- a3 + b3 + c3 = (a + b + c) (a2 + b2 + c2 – ab – bc – ca) + 3abc If a + b + c = 0, then a3 + b3 + c3 = 3abc
- (a+b+c)2 = a2+b2+c2+2ab+2bc+2ca
- (a+b+c)3 = a3+b3+c3+3a2 (b+c) + 3b2(a+b)+3c2(a+b)+6abc [remember there are ten terms]
- To find the sum of a and b, given their difference and product:
a + b = - To find the difference of a and b, given their sum and product: a – b =
Questions on Simplification
Generally, the types of questions that can be asked for simplification are of the following types.Type I: Questions Involving Addition or Subtraction (Integers/Decimals)
Problem 1:
Simplify: 563.5 + 128.7 - 300.2
Solution:
First, add 563.5 and 128.7:
563.5 + 128.7 = 692.2Now, subtract 300.2 from 692.2:
692.2 - 300.2 = 392Answer: 392
Type II: Questions Involving Fractions (Pure/Mixed)
Problem 2:
Simplify: 3 1/2 + 2 3/4 - 1 2/3
Solution:
First, convert the mixed fractions into improper fractions:
3 1/2 = 7/2
2 3/4 = 11/4
1 2/3 = 5/3Now, find the LCM of 2, 4, and 3 (LCM = 12) and convert all fractions:
7/2 = 42/12
11/4 = 33/12
5/3 = 20/12Now, simplify:
42/12 + 33/12 - 20/12 = (42 + 33 - 20)/12 = 55/12Convert back to a mixed fraction:
55/12 = 4 7/12Answer: 4 7/12
Type III: Questions Involving Multiplication or Division
Problem 3:
Simplify: 1.6 x 20 x 12 + 30 x 2
Solution:
First, solve the multiplication part:
1.6 x 20 = 32
32 x 12 = 384
30 x 2 = 60Now, add them together:
384 + 60 = 444Answer: 444
Problem 4:
Simplify: 2.21 ÷ 0.7 = ? + 5.5
Solution:
First, solve the division:
2.21 ÷ 0.7 = 3.157Now, solve for the unknown:
3.157 = ? + 5.5
? = 3.157 - 5.5 = -2.343Answer: -2.343
Problem 5:
Simplify: 4545 ÷ 50 ÷ 5
Solution:
First, divide 4545 by 50:
4545 ÷ 50 = 90.9Now, divide 90.9 by 5:
90.9 ÷ 5 = 18.18Answer: 18.18
Type IV: Questions Involving Percentage, Multiplication, Division, Fractions, etc.
Problem 6:
Simplify: 35% of 495 + ? = 250
Solution:
First, calculate 35% of 495:
35% of 495 = (35/100) x 495 = 0.35 x 495 = 173.25Now, solve for the unknown:
173.25 + ? = 250
? = 250 - 173.25 = 76.75Answer: 76.75
Problem 7:
Simplify: 30% of 150 + ? of 300 = 40% of 450
Solution:
First, calculate 30% of 150 and 40% of 450:
30% of 150 = 0.30 x 150 = 45
40% of 450 = 0.40 x 450 = 180Now, substitute these values into the equation:
45 + ? of 300 = 180
? of 300 = 180 - 45 = 135
? = 135 ÷ 300 = 0.45Answer: 0.45
Type V: Square Roots and Cube Roots
Problem 8:
Simplify: √25 + 3√16
Solution:
First, calculate the square roots:
√25 = 5
√16 = 4, so 3√16 = 3 x 4 = 12Now, add the results:
5 + 12 = 17Answer: 17
Type VI: Questions Involving Surds and Indices
Problem 9:
Simplify: (19.7)^5 ÷ (19.7)^4
Solution:
Using the property of exponents:
(a^m ÷ a^n) = a^(m-n)So,
(19.7)^5 ÷ (19.7)^4 = (19.7)^(5-4) = (19.7)^1 = 19.7Answer: 19.7
Problem 10:
Simplify: 2310.5 x 235.1 ÷ 231.2
Solution:
First, calculate the multiplication and division:
2310.5 x 235.1 = 543,853.55
Now, divide by 231.2:
543,853.55 ÷ 231.2 = 2,351.35Answer: 2,351.35
Type VII: Questions Involving Inequalities or Equalities
Problem 11:
Solve the inequality: 5x - 7 > 3x + 5
Solution:
First, move the terms involving x to one side:
5x - 3x > 5 + 7
2x > 12Now, divide by 2:
x > 6Answer: x > 6
Edurev Tip
- Always remember to follow the BODMAS rule to prioritize operations.
- Break down complex problems into smaller, manageable parts.
- Practice solving questions without a calculator to build speed and accuracy.
|
194 videos|840 docs|2228 tests
|
FAQs on Simplification - General Test Preparation for CUET UG - CUET Commerce
| 1. What are the general rules for solving problems in arithmetic simplification? |  |
| 2. How do I simplify arithmetic expressions involving parentheses? |  |
| 3. What is the order of operations in arithmetic simplification? |  |
| 4. Can you provide an example of simplifying an arithmetic expression using the order of operations? |  |
| 5. Are there any exceptions to the order of operations in arithmetic simplification? |  |





















