Solved Examples - Polynomials, Class 10, Mathematics | Extra Documents, Videos & Tests for Class 10 PDF Download
Ex.1 Find the zeros of the quadratic polynomial x2 + 7x + 12, and verify the relation between the zeros and its coefficients.
Sol. We have,
f(x) = x2 + 7x + 12 = x2 + 4x + 3x + 12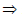 f(x) = x(x + 4) + 3 (x + 4)
f(x) = x(x + 4) + 3 (x + 4) f(x) = (x + 4) (x + 3)
f(x) = (x + 4) (x + 3)
The zeros of f(x) are given by f(x) = 0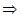 x2 + 7x + 12 = 0
x2 + 7x + 12 = 0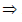 (x + 4) (x + 3) = 0
(x + 4) (x + 3) = 0 x + 4 = 0 or, x + 3 = 0
x + 4 = 0 or, x + 3 = 0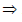 x = – 4 or x = – 3
x = – 4 or x = – 3
Thus, the zeros of f(x) = x2 + 7x + 12 are α = – 4 and β = – 3
Now, sum of the zeros =α+β = (–4) + (–3) = – 7

Ex.2 Find the zeros of the quadratic polynomial f(x) = abx2 + (b2 + ac) x + bc and verify the relationship between the zeros and its coefficients.
Sol. f(x) = abx2 + (b2 + ac) x + bc = abx2 + b2x + acx + bc
= bx (ax + b) + c (ax + b) = (ax + b) (bx + c)
So, the value of f(x) is zero when ax + b = 0 or bx + c = 0, i.e. x = –b/a or x = –c/b
Therefore, –b/a and –c/b are the zeros (or roots) of f(x).



Ex.3 Find a quadratic polynomial each with the given numbers as the sum and product of its zeros respectively.
(i) 14 , –1 (ii) 2 , 13
Sol. We know that a quadratic polynomial when the sum and product of its zeros are given is given by –
f(x) = k {x2 – (Sum of the zeros) x + Product of the zeros}, where k is a constant.
(i) Required quadratic polynomial f(x) is given by f(x) = k (x2 – 1/4 x – 1 )
(ii) Required quadratic polynomial f(x) is given by f(x) = k (x2 – √ x 1/3 )
Ex.4 Divide the polynomial 2x2 + 3x + 1 by the polynomial x + 2 and verify the division algorithm.
Sol. We have

Clearly, quotient = 2x – 1 and remainder = 3
Also, (x + 2) (2x – 1) + 3 = 2x2 + 4x – x – 2 + 3 = 2x2 + 3x + 1
i.e., 2x2 + 3x + 1 = (x + 2) (2x–1) + 3. Thus, Dividend = Divisor × Quotient + Remainder.
Ex.5 Check whether the polynomial t2 – 3 is a factor of the polynomial 2t4 + 3t3 – 2t2 – 9t – 12, by dividing the second polynomial by the first polynomial.
Sol. We have

Since the remainder is zero, therefore, the polynomial t2 – 3 is a factor of the polynomial 2t4 + 3t3 – 2t2 – 9t – 12
Ex.6 Find all the zeros of 2x4 – 3x3 – 3x2 + 6x – 2, if you know that two of its zeros are √2 and – √2.
Sol. Let p(x) = 2x4 – 3x3 – 3x2 + 6x – 2 be the given polynomial. Since two zeros are √2 and – √2 so, (x –√2 ) and (x+√2 ) are both factors of the given polynomial p(x).
Also, (x – √2) (x + √2) = (x2 – 2) is a factor of the polynomial. Now, we divide the given polynomial by x2 – 2.


Hence, all the zeros of the polynomial 2x4 – 3x3 – 3x2 + 6x – 2 are √2 , – √2 , 1 and 1/2
Ex.7 On dividing f(x) = x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4,
respectively. Find g(x).
Sol. Here, Dividend = x3 – 3x2 + x + 2
Quotient = x – 2,
Remainder = – 2x + 4 and Divisor = g(x).
Since Dividend = Divisor × Quotient + Remainder
So, x3 – 3x2 + x + 2 = g(x) × (x –2) + (–2x + 4)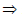 g(x) × (x – 2) = x3 – 3x2 + x + 2 + 2x – 4
g(x) × (x – 2) = x3 – 3x2 + x + 2 + 2x – 4

Ex.8. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2 .
Sol.

Hence, Quotient q(x) = x – 3 and Remainder r(x) = 7x – 9
Ex.9. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the
first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12 (ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Sol:

Hence, t2– 3 is a factor of 2t4+ 3t3 – 2t2 – 9t – 12
Ex.10. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0.
Sol. (i) p(x) = 2x2 + 2x + 8, g(x) = 2x0 = 2; q(x) = x2 + x + 4 ; r(x) = 0
(ii) p(x) = 2x2 + 2x + 8 ; g(x) = x2 + x + 9 ; q(x) = 2 ; r(x) = – 10
(iii) p(x) = x3 + x + 5 ; g(x) = x2 + 1 ; q(x) = x ; r(x) = 5.
|
5 videos|292 docs|59 tests
|
FAQs on Solved Examples - Polynomials, Class 10, Mathematics - Extra Documents, Videos & Tests for Class 10
| 1. What are polynomials in mathematics? |  |
| 2. How do you classify polynomials based on the number of terms? |  |
| 3. What is the degree of a polynomial and how is it determined? |  |
| 4. How are polynomials added and subtracted? |  |
| 5. How do you multiply polynomials? |  |























