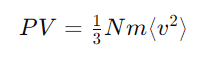Kinetic Theory of Gases | Chemistry for JEE Main & Advanced PDF Download
| Table of contents |

|
| What is Kinetic Theory of Gases? |

|
| The Kinetic Equation |

|
| Distribution of Molecular Velocities |

|
| Solved Examples |

|
What is Kinetic Theory of Gases?
The kinetic molecular theory explains the behavior of gases by describing the motion and interactions of gas particles at a microscopic level. The kinetic theory of gases is a fundamental theory in physics that explains the behavior of gases in terms of the motions of their individual molecules.
The kinetic theory of gases explains the behavior of gases by considering them as a large number of small particles (atoms or molecules) in constant, random motion. It states that the pressure exerted by a gas results from collisions of the particles with the walls of the container. The theory also relates the macroscopic properties of gases, such as temperature and pressure, to the microscopic motions and interactions of the particles.
Here are the main ideas, each with an explanation:
Tiny Particles:
- Gases are composed of a large number of tiny particles (atoms or molecules).
- These particles are so small and so far apart that their own volume is negligible compared to the space between them. This assumption helps explain why gases can be compressed easily.
- When we compress a gas, we are simply pushing these widely spaced particles closer together without them taking up much more space.
No Forces of Attraction:
- Gas particles do not exert any attractive forces on each other under normal conditions of temperature and pressure.
- This lack of attraction is evident because gases expand to fill any container they are placed in.
- If there were significant attractive forces, the particles would clump together instead of spreading out.
Constant Motion:
- Gas particles are always moving randomly and constantly.
- This random motion prevents the gas from having a fixed shape, unlike solids. If gas particles were stationary, they would settle and the gas would have a definite shape, which is not observed.
Straight-Line Movement:
- Gas particles move in straight lines until they collide with each other or the walls of their container.
- These collisions cause the particles to change direction, but between collisions, their motion remains in straight lines.
- The pressure exerted by the gas is due to these collisions with the container walls.
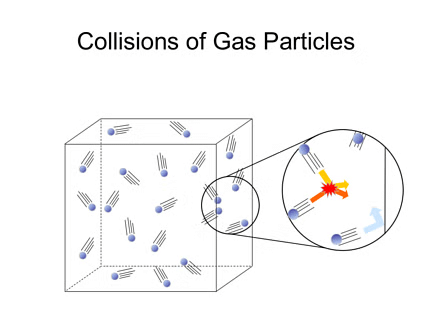
Elastic Collisions:
- When gas particles collide, the collisions are perfectly elastic, meaning there is no loss of total kinetic energy.
- While the energy of individual particles can change during a collision (one particle may speed up while the other slows down), the total energy of all particles remains the same.
- If collisions were not elastic, particles would lose energy over time, eventually stopping, which does not happen in reality.
Variable Speeds:
- At any given moment, gas particles have different speeds and therefore different kinetic energies.
- This variation is due to the constant collisions between particles, which change their speeds. Even if all particles started with the same speed, collisions would quickly lead to a range of speeds.
- Despite this, the overall distribution of speeds remains constant at a given temperature.
Average Kinetic Energy:
- The average kinetic energy of gas particles is directly proportional to the absolute temperature of the gas.
- As the temperature increases, the average kinetic energy of the particles increases.
- This means that particles move faster and collide more frequently and with greater force, leading to an increase in pressure if the volume of the gas is kept constant. This relationship helps explain why heating a gas at constant volume increases its pressure.
The Kinetic Equation
The kinetic equation is a mathematical expression that relates the macroscopic properties of a gas (such as pressure, volume, and temperature) to the microscopic properties (such as the velocity and mass of gas molecules) as described by the kinetic molecular theory.
The equation derived from the kinetic theory of gases is:
- P = Pressure of gas
- V = Volume of gas
- m = mass of one molecule of gas
- N = no. of molecules of gas
- v = root mean square velocity of molecules
For 1 mole n = N (Avogadro number)
m x N = Molecular mass M.
or
Distribution of Molecular Velocities
Maxwell and Boltzmann proposed that gas molecules are always in rapid random motion colliding with each other and with the walls of container. Due to such collisions, their velocities always changes. A fraction of molecules have a particular molecular velocity at a time. James Clark Maxwell calculated the distribution of velocity among fraction of total number of molecules, on the basis of probability.
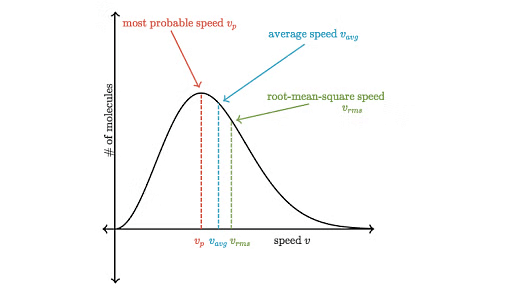
The distribution of velocities of different gas molecules may be shown by the following curve.
 Maxwell Boltzmann Curve
Maxwell Boltzmann Curve
From the curve it may be concluded that
(i) Only a small fraction of molecules have either very low or very high velocity.
(ii) Curve becomes flat when temperature is raised i.e. distribution around average velocity becomes wider. Average molecular velocity increases with rise in temperature.
(iii) Most of the molecules have velocity close to most probable velocity represented by the top of curve.
(iv) At higher temperature, greater number of molecules have high velocity, while few molecules have lower velocity.
- Average Velocity : As per kinetic theory of gases, each molecule is moving with altogether different velocity. Let `n' molecules be present in a given mass of gas, each one moving with velocity u1,u2, u3, …,un. The average velocity or Uav = average of all such velocity terms.
Average velocity = - Root Mean Square Velocity : Maxwell proposed the term as the square root of means of square of all such velocities.
Also - Most probable velocity: It is the velocity possessed by maximum no. of molecules.
Furthermore
=
= 1 : 1.128 : 1.224
Kinetic Energy of Gas: As per kinetic equation
For 1 mole m x n = Molecular Mass (M)
or
Also KE per molecule Where k is the Boltzmann constant
Kinetic Energy of gas sample:
(i) Average kinetic energy of a single molecule = T = KT
K = boltzman constant = 1.38 x 10-23 J/deg
(ii) total Kinetic Energy for one mole of gas = RT
(iii) kinetic Energy for n mol of gas = n x RT
Solved Examples
Example: Calculate rms speed of O2 at 273 K and 1 x 105 Pa pressure. The density of O2 under these conditions is 1.42 kg m-3.
Solution: Data are given in SI units
Example: At what temperature will the r.m.s. velocity of oxygen be one and half times of its value at N.T.P.?
Solution:
Suppose the temperature required is
then the velocity will be
Example: Calculate the average and total kinetic energy of 0.5 mole of an ideal gas at 0xC.
Solution: Average kinetic energy =
KT =
x1.38 x10-23 x 273 = 5.65x 10-21J
Total kinetic energy of n mole of gas = n x
RT = 0.5 x
x 8.314 x 273
= 1.702kJ
|
366 videos|847 docs|301 tests
|
FAQs on Kinetic Theory of Gases - Chemistry for JEE Main & Advanced
| 1. What is the Kinetic Theory of Gases? |  |
| 2. How does temperature affect the kinetic energy of gas particles? |  |
| 3. What is the relationship between the volume of a gas and its pressure according to the Kinetic Theory of Gases? |  |
| 4. How does the mass of gas particles affect the average kinetic energy of a gas? |  |
| 5. Can gas particles have different speeds in the same sample of gas? |  |