Dimensional Analysis & Formulas | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Dimensional Analysis |

|
| Dimensional Formula |

|
| Applications of Dimensional Analysis |

|
| Limitations of Dimensional Analysis |

|
Dimensional Analysis
Dimensions of a physical quantity are the power to which the fundamental quantities must be raised to represent the given physical quantity.
 Dimensional Analysis
Dimensional Analysis
- Mass is usually represented by M, length by L, time by T, and electric current by A.
- The unit symbols for thermodynamic temperature, amount of substance, and luminous intensity are K, mol, and cd respectively.
- Physical quantities expressed in terms of base quantities are shown in square brackets, for example, [sinθ] = [cosθ] = [tanθ] = [ex] = [M0L0T0]
Dimensional Formula
A dimensional formula is a way to express the fundamental units required to represent a physical quantity. It shows how a particular quantity is related to the basic dimensions of mass, length, time, etc.
For instance:
- Velocity is a derived quantity that indicates the rate of change of displacement over time. The dimensional formula for velocity can be expressed as:
Velocity = Displacement / Time
Displacement is measured in terms of length, denoted as [L 1 ], and time is measured as [T 1 ]. These are fundamental quantities. Therefore, the dimensional formula for velocity can be written as:
[v] = [s/t] = [L/T] = [LT -1 ]
Similarly, we can evaluate the dimensional formula of all physically derived quantities. The table given below shows some of the most occurring physical quantities and their dimensions.
Different Quantities with Their Units, Symbols, and Dimensional Formulas


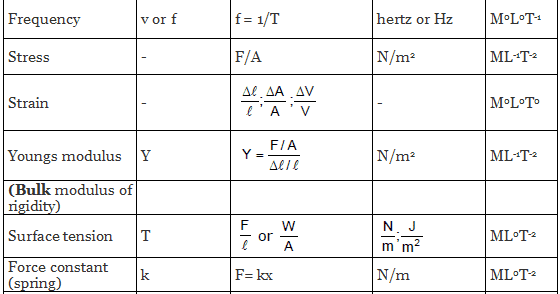
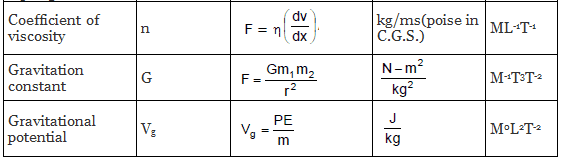
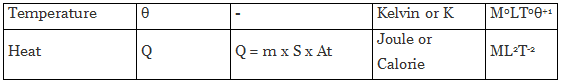

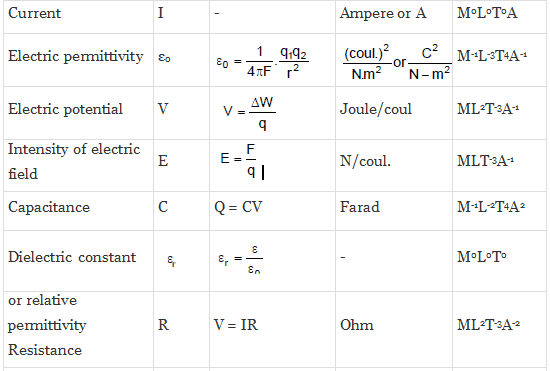
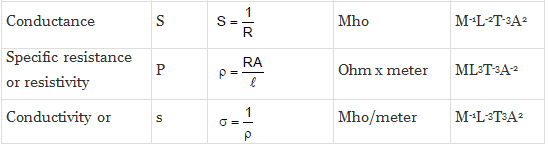
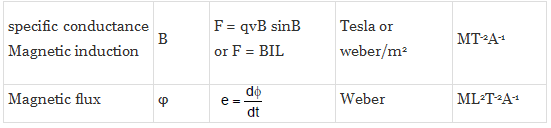

Applications of Dimensional Analysis
Conversion of units
This is based on the fact that the product of the numerical value (n) and its corresponding unit (u) is a constant, i.e.,
n[u] = constant
or n1[u1] = n2 [u2]
Suppose the dimensions of a physical quantity are a in mass, b in length, and c in time. If the fundamental units in one system are M1, L1, and T1 and in the other system are M2, L2, and T2 respectively. Then we can write.
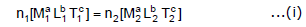 Here n1 and n2 are the numerical values in two systems of units respectively.
Here n1 and n2 are the numerical values in two systems of units respectively.
Using Eq. (i), we can convert the numerical value of a physical quantity from one system of units into the other system.
Example 1. The value of the gravitation constant is G = 6.67 × 10-11 Nm2/kg2 in SI units. Convert it into CGS system of units.
Solution. The dimensional formula of G is [M-1 L3 T-2].
Using equation number (i), i.e.,
Here, n1 = 6.67 x 10-11
M1 = 1 kg, M2 = 1 g = 10-3 kg, L1 = 1 m, L2 = 1 cm = 10-2 m, T1 = T2 = 1s
Substituting in the above equation, we get
or n2 = 6.67 x 10-8
Thus, the value of G in the CGS system of units is 6.67 x 10-8 dyne cm2/g2.
To check the dimensional correctness of a given physical equation
- Every physical equation should be dimensionally balanced. This is called the 'Principle of Homogeneity'.
- The dimensions of each term on both sides of an equation must be the same. On this basis, we can judge whether a given equation is correct or not. However, a dimensionally correct equation may or may not be physically correct.
Example 2. Show that the expression of the time period T of a simple pendulum of length l given by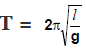
is dimensionally correct.
Solution. 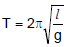
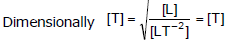 As in the above equation, the dimensions of both sides are the same. The given formula is dimensionally correct.
As in the above equation, the dimensions of both sides are the same. The given formula is dimensionally correct.
Principle of Homogeneity of Dimensions
This principle states that the dimensions of all the terms in a physical expression should be the same. For example, in the physical expression s = ut + 1/2 at2, the dimensions of s, ut, and 1/2 at2 all are the same.
Note: The physical quantities separated by the symbols +, -, =, >, <, etc., have the same dimensions.
Example 3. The velocity v of a particle depends upon the time t according to the equation 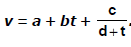 .
.
Write the dimensions of a, b, c, and d.
Solution.
From the principle of homogeneity
To establish the relation among various physical quantities
If we know the factors on which a given physical quantity may depend, we can find a formula relating the quantity to those factors. Let us take an example.
Example.4. The frequency (f) of a stretched string depends upon the tension F (dimensions of force), length l of the string, and the mass per unit length m of string. Derive the formula for frequency.
Solution. Suppose, that the frequency f depends on the tension raised to the power a, length raised to the power b, and mass per unit length raised to the power c. Then.
f ∝ [F]a[l]b[μ]c
or f = k[F]a[l]b[μ]c
Here, k is a dimensionless constant. Thus,
[f] = [F]0[l]b[μ]c
or [M0L0T-1] = [MLT-2]a[L]b[ML-1]c
or [M0L0T-1] = [Ma+c La+b-c T-2a]
For dimensional balance, the dimensions on both sides should be the same.
Thus, a + c = 0 ...(ii)
a + b - c = 0 ...(iii)
and - 2a = - 1 ...(iv)
Solving these three equations, we get
a = 1/2, c = (-1/2) and b = -1
Substituting these values in Eq. (i), we get
f = k(F)1/2(l)-1(μ)-1/2
orExperimentally, the value of k is found to be 1/2.
Limitations of Dimensional Analysis
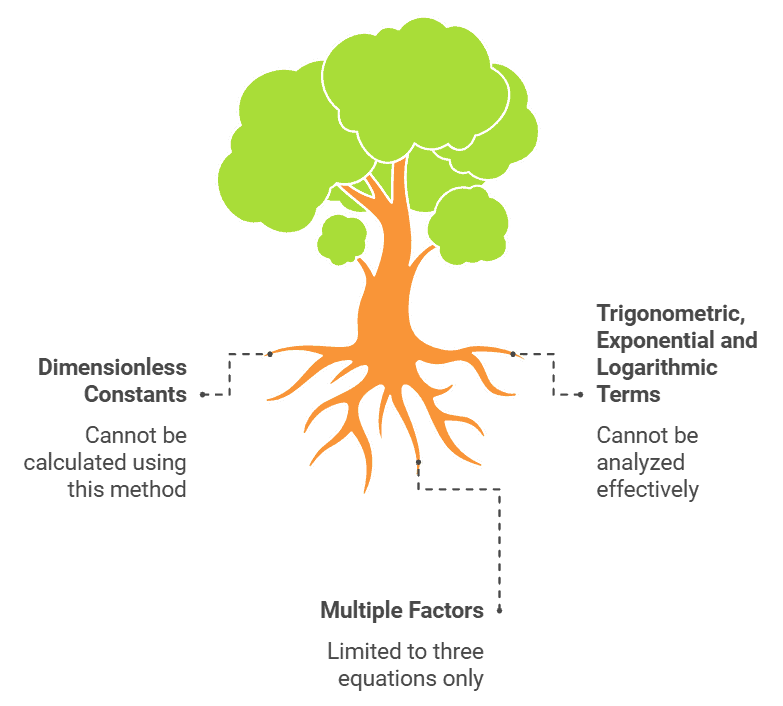 LimitationsThe method of dimensions has the following limitations:
LimitationsThe method of dimensions has the following limitations:
(a) By this method the value of dimensionless constant can not be calculated.
(b) By this method the equation containing trigonometrical, exponential, and logarithmic terms cannot be analyzed.
(c) If a physical quantity depends on more than three factors, then a relation among them cannot be established because we can have only three equations by equalizing the powers of M, L, and T.
|
96 videos|367 docs|98 tests
|
FAQs on Dimensional Analysis & Formulas - Physics Class 11 - NEET
| 1. What is dimensional analysis and why is it important in physics? |  |
| 2. What are the basic dimensions used in dimensional analysis? |  |
| 3. How can dimensional analysis be applied to derive physical formulas? |  |
| 4. What are some limitations of dimensional analysis? |  |
| 5. Can dimensional analysis be used in fields outside of physics? |  |





















