Internal Work & Conservative Force | Physics for JAMB PDF Download
6. Internal Work :
Suppose that a man sets himself in motion backward by pushing against a wall. The forces acting on the man are his weight 'W' the upward force N exerted by the ground and the horizontal force N exerted by the wall. The works of 'W' and of N are zero because they are perpendicular to the motion. The force N' is the unbalanced horizontal force that imparts to the system a horizontal acceleration. The work of N', however, is zero because there is no motion of its point of application. We are therefore confronted with a curious situation in which a force is responsible for acceleration, but its work, being zero, is not equal to the increase in kinetic energy of the system.
The new feature in this situation is that the man is a composite system with several parts that can move in relation to each other and thus can do work on each other, even in the absence of any interaction with externally applied forces. Such work is called internal work. Although internal forces play no role in acceleration of the composite system, their points of application can move so that work is done; thus the man's kinetic energy can change even though the external forces do no work.
"Basic concept of work lies in following lines
Draw the force at proper point where it acts that give proper importance of the point of application of force.
Think independently for displacement of point of application of force, Instead of relation the displacement of applicant point with force relate it with the observer or reference frame in which work is calculated.

7. Conservative force :
A force is said to be conservative if work done by or against the force in moving a body depends only on the initial and final positions of the body and does not depend on the nature of path followed between the initial and final positions.
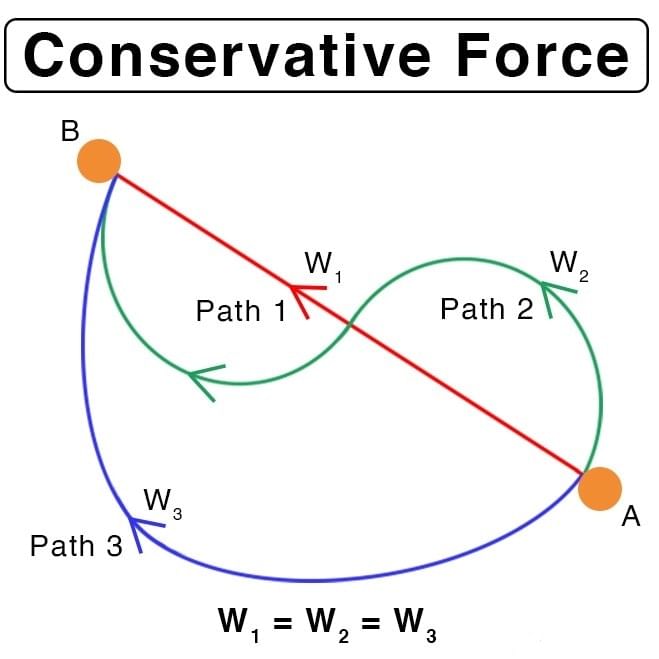
Consider a body of mass m being raised to a height h vertically upwards as shown in above figure. The work done is mgh. Suppose we take the body along the path as in (b). The work done during horizontal motion is zero. Adding up the works done in the two vertical parts of the paths, we get the result mgh once again. Any arbitrary path like the one shown in (c) can be broken into elementary horizontal and vertical portions. Work done along the horizontal path is zero. The work done along the vertical parts add up to mgh. Thus we conclude that the work done in raising a body against gravity is independent of the path taken. It only depends upon the initial and final positions of the body. We conclude from this discussion that the force of gravity is a conservative force.
Examples of Conservative forces.
(i) Gravitational force, not only due to Earth due in its general form as given by the universal law of gravitation, is a conservative force.
(ii) Elastic force in a stretched or compressed spring is a conservative force.
(iii) Electrostatic force between two electric charges is a conservative force.
(iv) Magnetic force between two magnetic poles is a conservative force.
Forces acting along the line joining the centers of two bodies are called central forces. Gravitational force and Electrostatic forces are two important examples of central forces. Central forces are conservative forces.
Properties of Conservative forces
- Work done by or against a conservative force depends only on the initial and final position of the body.
- Work done by or against a conservative force does not depend upon the nature of the path between initial and final position of the body.
- Work done by or against a conservative force in a round trip is zero.
- If a body moves under the action of a force that does no total work during any round trip, then the force is conservative; otherwise it is non-conservative.
- The concept of potential energy exists only in the case of conservative forces.
- The work done by a conservative force is completely recoverable.
Complete recoverability is an important aspect of the work done by a conservative force.
Work done by conservative forces
Ist format : (When constant force is given)
Ex.8 Calculate the work done to displace the particle from (1, 2) to (4, 5). if 
Sol.
w = (16 - 4) + (15 - 6) = w = 12 + 9 = 21 Joule
II format : (When F is given as a function of x, y, z)
then
Ex.9 An object is displaced from position vector under a force
Find the work done by this force.
Sol.
IIIrd format (perfect differential format)
then find out the work done in moving the particle from position (2, 3) to (5, 6)
Sol.
Now ydx + xdy = d(xy) (perfect differential equation)
⇒ dw = d(xy)
for total work done we integrate both side
⇒ w = (30 - 6) = 24 Joule
8. Non-conservative forces :
A force is said to be non-conservative if work done by or against the force in moving a body depends upon the path between the initial and final positions.
The frictional forces are non-conservative forces. This is because the work done against friction depends on the length of the path along which a body is moved. It does not depend only on the initial and final positions. Note that the work done by frictional force in a round trip is not zero.
The velocity-dependent forces such as air resistance, viscous force, magnetic force etc., are non conservative forces.
Ex.11 Calculate the work done by the force to move the particle from (0, 0) to (1, 1) in the following condition
(a) y = x (b) y = x2
Sol. We know that
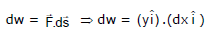
dw = ydx ...(1)
In equation (1) we can calculate work done only when we know the path taken by the particle.
either
y = x or y = x2 so now
(a) when y = x
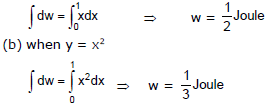
Difference between conservative and Non-conservative forces
s. No. | Conservative forces | Non-Conservative forces |
1 | Work done does not depend upon path | Work done depends on path. |
2 | Work done in a round trip is zero. | Work done in a round trip is not zero. |
3 | Central in nature. | Forces are velocity- dependent and retarding in nature. |
4 | W'hen only a conservative force acts within a system, the kinetic energy and potential energy can change. However their sum, the mechanical energy of the system, does not change. | Work done against a non conservative force may be dissipated as heat energy. |
5 | Work done is completely recoverable. | Work done in not completely recoverable. |
|
260 videos|253 docs|230 tests
|
















