Work-Energy Theorem for a Variable Force | Physics for ACT PDF Download

Work Energy Theorem

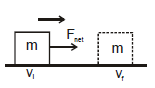
If the resultant or net force acting on a body is F_net then Newton's second law states that
F_net = ma ...(1)
If the resultant force varies with x, the acceleration and speed also depend on x.

Work done by net force F_net in displacing a particle equals to the change in kinetic energy of the particle.

i.e. we can write eq. (3) in following way
(W.D)_C + (W.D)_N.C + (W.D)_ext. + (W. D)_pseudo

= ΔK ...(4)

where (W.D)_C = work done by conservative force
(W. D)_N.C = work done by non conservative force.
(W.D)_ext = work done by external force
(W.D)_pseudo = work done by pseudo force, we know that

we know that
(W.D)_c = - ΔU
⇒ - ΔU + (W.D)_N.C + (W.D)_ext (W.D)_pseudo = ΔK
= (W.D)_N.C + (W.D)_ext + (W.D)_pseudo - (k_f + u_f) - (k_i + u_i)
∴ k 4+ u = Mechanical energy.

=> work done by forces (except conservative forces) = change is mechanical energy.
If (W.D)_N.C = (W.D)_ext = (W.D)_pseudo = 0
= K_f + U_f = K_i + U_i

Initial mechanical energy = final mechanical energy

This is called mechanical energy conservation law.

Questions Based on work Energy Theorem : 

Ex.14 The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m. 

Sol.

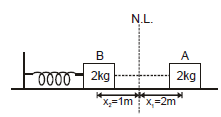
In the above problem only one conservative force (spring force) is working on the block so from mechanical energy conservation

at A block is at rest so k_i = 0

At position B if speed of the block is v then

Putting the above values in equation (i), we get

Ex.15 A block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
Sol.

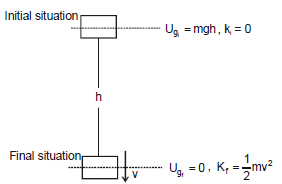
Figure shows the complete description of the problem only one conservative force is working on the block. So from mechanical energy conservation

k_f + u_f = k_i + u_i

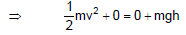
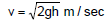
(B) When two conservative force are acting in problem. 

Ex.16 One end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37º with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. [sin 37º = 3/5] 

Sol. If l is the stretched length of the spring, then from figure

Now, taking point B as reference level and applying law of conservation of mechanical energy between A and B,

E_A = E_B

or
[as for, B, h = 0 and y = 0]

or
  Ans.

Ex.17 The block shown in figure is released from rest and initially the spring is at its natural length. Write down the energy conservation equation. When the spring is compressed by l₁ ?

Sol. Here two conservative forces are included in the problem.
(i) Gravitational force (ii) spring force
We assume zero gravitational potential energy at A as shown in figure.

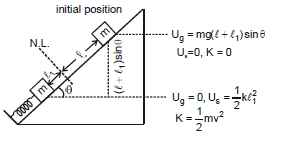
from mechanical energy conservation

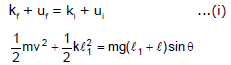
(C) When only one non conservative force is included in problem. 

Ex.18 Find out the distance travelled by the block as shown in figure. If the initial speed of the block is v and m is the friction coefficient between the surface of block and ground. 

Sol. Applying work energy theorem, we get

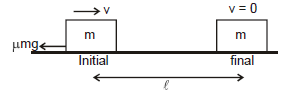
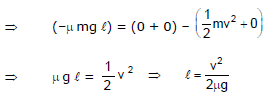
(D) When both conservative and non-conservative force in the problem 

Ex.19 A particle slides along a track with elevated ends and a flat central part as shown in figure. The flat portion BC has a length l = 3.0 m. The curved portions of the track are frictionless. For the flat part the coefficient of kinetic friction is m_k = 0.20, the particle is released at point A which is at height h = 1.5 m above the flat part of the track. Where does the particle finally comes to rest?
Sol. As initial mechanical energy of the particle is mgh and final is zero, so loss in mechanical energy

= mgh. This mechanical energy is lost in doing work against friction in the flat part,
So, loss in mechanical energy = work done against friction

or mgh = mmgs i.e., s =  =  = 7.5 m

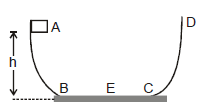
After starting from B the particle will reach C and then will rise up till the remaining KE at C is converted into potential energy. It will then again descend and at C will have the same value as it had when ascending, but now it will move from C to B. The same will be repeated and finally the particle will come to rest at E such that
BC + CB + BE = 7.5
or 3 + 3 + BE = 7.5
i.e., BE = 1.5

So, the particle comes to rest at the centre of the flat part.

Ex.20 A 0.5 kg block slides from the point A on a horizontal track with an initial speed 3 m/s towards a weightless horizontal spring of length 1 m and force constant 2 N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as 0.22 and 0.20 respectively. If the distance AB and BD are 2 m and 2.14 m respectively, find the total distance through which the block moves before it comes to rest completely. [g = 10 m/s²] 

Sol. As the track AB is frictionless, the block moves this distance without loss in its initial

KE =  =  × 0.5 × 3² = 2.25 J. In the path BD as friction is present, so work done against friction

= m_k mgs = 0.2 × 0.5 × 10 × 2.14 = 2.14 J

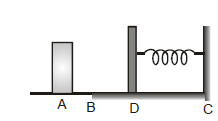
So, at D the KE of the block is = 2.25 - 2.14 = 0.11 J.

Now, if the spring is compressed by x

0.11 =  × k × x²+ m_k mgx

i.e., 0.11 =  × 2 × x² 0.2 × 0.5 × 10x

or x² + x - 0.11 = 0

which on solving gives positive value of x = 0.1 m

After moving the distance x = 0.1 m the block comes to rest. Now the compressed spring exerts a force :

F = kx = 2 × 0.1 = 0.2 N

on the block while limiting frictional force between block and track is f_L = m_s mg = 0.22 × 0.5 × 10 = 1.1 N.

Since, F < f_L. The block will not move back. So, the total distance moved by block

= AB + BD +  0.1

= 2 +  2.14 + 0.1

= 4.24 m

(E) Important Examples : 

Ex.21 A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the paritcle with respect to the sphere as a function of the angle q it slides. 

Sol. We solve the above problem with respect to the sphere. So apply a pseudo force on the particle

Now from work energy theorem.

work done by ma = change in mechanical energy

⇒ ma R sinθ = (k_f + u_f) - (k_i +  u_i)

maR sinθ =  ⇒  = maR sinθ +  mgR (1 - cosθ)

⇒ v² = 2R(a sinθ +  g - g cosθ) ⇒ v = [2R (a sinθ +  g - g cosθ)]^1/2 m/sec

Ex.22 In the arrangement shown in figure m_A = 4.0 kg and m_B = 4.0 kg. The system is released from rest and block B is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of friction between the block and the table.
 Neglect friction elsewhere. (Take g = 10 m/s²) 

Sol. From constraint relations, we can see that
v_A = 2 v_B
Therefore, v_A = 2(0.3) = 0.6 m/s
as v_B = 0.3 m/s (given)
Applying W_nc = DU + DK
we get - m m_A g S_A = - m_B g S_B + m_Av_A² + m_Bv_B²
Here, S_A = 2S_B = 2m as S_B = 1 m (given)
- m(4.0) (10) (2) = - (1) (10) (1) + (4) (0.6)² +  (1) (0.3)²
or - 80 m = - 10 + 0.72 +  0.045 or 80m = 9.235 or m = 0.115 Ans. 

Vertical Circular Motion

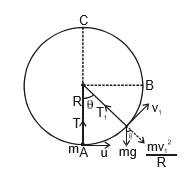
Now we study the circular motion of the body in two parts.
A) Motion of a body from A to B.
B) Motion of a body from B to C.

A. Motion of a body from A to B.

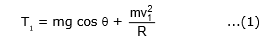
During the motion of the body from A to B.

q will increase so cosθ will decrease.

Due to which mg cosθ will decrease. From A to B speed of the body also decreases due to which decreases. Therefore tenstion in the string decreases from A to B.

But due to mg cosθ tension can never be zero.

B. Motion of a body from B to C.

from  B → C

speed decreases due to which  decreases.

9 decreases due to which mg cos 9 increases. Therefore from B → C. Tension in the string decreases.

String slacks at a point where  = mg cos θ i.e.,T = 0

13.1 Minimum velocity at point A for which body can complete the vertical circle 

The condition for the body to complete the vertical circle is that the string should be taut all the time i.e. the tension is greater than zero.

So the body can complete the vertical circle if the tension is not zero in between the region B to C.

Initially.

Apply energy conservation from A to C then

body can complete vertical circle, when

Put the value from (3) to (2) and

It the velocity is greater than equal to  then the body will complete the vertical circle.

Tension at A

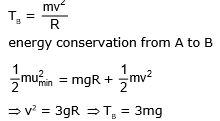
Tension at B

energy conservation from A to B

13.2 Condition for the body to reach B :

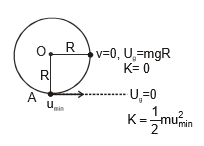
Let us calculate the u_min such that the body just reaches B.
Work done by tension = 0
Only gravitational force is working on the body which is a conservative force. Therefore Applying conservation of energy, we get

 then the body will oscillate about A.

13.3 When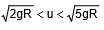  

If the velocity of projection is greater than  but less than 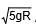, the particle rises above the horizontal diameter and the tension vanishes before reaching the highest point.

We have seen that the tension in the string at the highest point is lower than the tension at the lowest point.

At the point D, the string OD makes an angle f with the vertical. The radial component of the weight is mg cos f towards the centre O.

 .......(i)

Kinetic energy at

Potential energy at D = mg(AN)
= mg (AO + ON) ⇒ mg(R + R cosφ) = mg(R + R cosφ)
From conservation of energy

Substituting in equation (i),

This equation shows that the tension becomes zero, if

If the tension is not to become zero.

Equation (ii) gives the values of $ at which the string becomes slack.

It is the angle from the vertical at which tension in the string vanishes to zero. And after that its motion is projectile.

13.4 Tension in the string versus q 

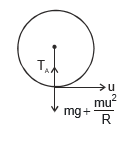
We may find an expression for the tension in the string when it makes an angle q with the vertical. At C, the weight of the body acts vertically downwards, and the tension in the string is towards the centre O.

The weight mg is resolved radially and tangentially.

The radial component is mg cosθ and the tangential component is mg sinθ.

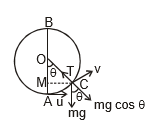
T - mg cos , where v is the velocity at C,

    ......(i)
The velocity v can be expressed in terms of velocity u at A.

The total energy at

The kinetic energy at  

The potential energy at C = mg (AM)
= mg (AO - MO)
= mg (R - R cosθ)
= mgR (1 - cos θ)

The total energy at

∴ From conservation of energy

u² - v² + 2gR (1 - cos θ) or v² = u² - 2gR(l - cos θ)

Substituting in equation (v),

This expression gives the value of the tension in the string in terms of the velocity at the lowest point and the angle θ. Equation (i) shows that tension in the string decreases as & increases, since the term 'g cos θ' decreases as θ increases.

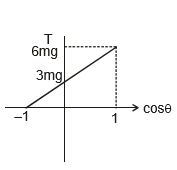
⇒ T = 3mg (1 + cos θ)
Now θ = 0 ⇒ cos θ = 1    ⇒ T_A = 6 mg
if, θ = 90° ⇒ T_B = 3 mg
θ = 180°, cos θ = - 1
T_c = 0

13.5 Different situations:
(A) A BODY MOVING INSIDE A HOLLOW TUBE OR SPHERE 

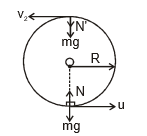
The previous discussion holds good for this case, but instead of tension in the string we have the normal reaction of the surface. If N is the normal reaction at the lowest point, then the condition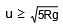 for the body to complete the circle holds for this case also. All other equations (can be) similarly obtained by replacing tension T by normal reaction N.

(B) When Body is attached to a rod of length R
In this case since the body is attached to a rigid rod. The body can not leave the circular path.

Therefore, if the speed of the body becomes zero before the highest point C. It's motion will be oscillatory about the centre of the rod.

Condition for completing the circle:
If the body just reaches the highest point then it will completes the vertical circle

Applying energy conservation between the lowest and highest point of circle, we get

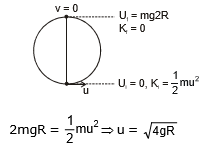
So, If the velocity at point A is greater than equal to  then body will compete the vertical circle.

(C) Vertical Motion in a Dual Ring 

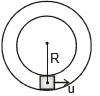
This system will behave as the preivious system. So u_min to complete vertical circle

Angle at which the normal reaction on the body will change its direction from inward to outward the ring is given by

(D) BODY MOVING ON A SPHERICAL SURFACE 

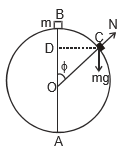
The small body of mass m is placed on the top of a smooth sphere of radius R and the body slides down the surface.

At any instant, i.e., at point C the forces are the normal reaction N and the weight mg. The radial component of the weight is mgcos f acting towards the centre. The centripetal force is

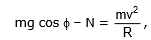
The body flies off'the surface at the point where N becomes zero.

To find v, we use conservation of energy

From equation (ii) and (iii) we get

This gives the angle at which the body goes of the surface. The height from the ground of that point AD = R(1 + cos φ)