Solved Examples: Constraint Equations | Physics for JEE Main & Advanced PDF Download
Constraint Equations

We know the cases where different blocks of the system had a common acceleration and that common acceleration was given by

Now, the question is, if different blocks have different accelerations then what? In those cases, we take the help of constraint equations. These equations establish the relation between accelerations (or velocities) of different blocks of a system.
Depending upon different kinds of problems we have divided the constraint equations in following two types.
1. String Constraint
When the two objects are connected through a string and if the string has the following properties:
(i) The length of the string remains constant i.e., it is an inextensible string.
(ii) Always remains taut i.e., does not slack.
Then the parameters of the motion of the objects along the length of the string have a definite relation between them.
➢ Type 1 (When String is Fixed)
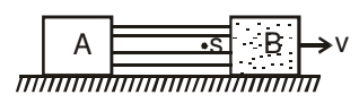
Block B moves with velocity v i.e. each particle of block B moves with velocity v.
If string remain attached to block B it is necessary that velocity of each particle of string is same = v (vs = v)
Now we can say that Block A also moves with velocity v.

Note: If pulley is fixed then the velocity of all the particles of string is same along the string.
➤ Example.1. Using constraint method find the relation between accelerations of 1 and 2.

Solution. At any instant of time let x1 and x2 be the displacements of 1 and 2 from a fixed line (shown dotted).
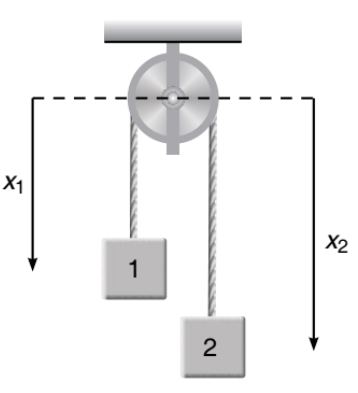
Here x1 and x2 are variables but,
⇒ x1+ x2 = constant
⇒ x1+ x2 = l (length of string)
Differentiating with respect to time, we have
⇒ v1 + v2 = 0
⇒ v1=-v2
Again differentiating with respect to time, we get
⇒ a1 + a2 = 0
⇒ a1= -a2
This is the required relation between a1 and a2, i.e. accelerations of 1 and 2 are equal but in opposite directions.
Note:
(i) In the equation x1+ x2 =l we have neglected the length of string over the pulley. But that length is also constant.(ii) In constraint equation if we get a1=- a2 then negative sign does not always represent opposite directions of a1 and a2. The real significance of this sign is, x2 decreases if x1 increases and vice-versa.
➤ Example.2. Using constraint equations find the relation between a1 and a2

Solution. In Figure points 1, 2, 3 and 4 are movable. Let their displacements from a fixed dotted line be x1 x2 x3 and x4
 x1+ x3 = l1
x1+ x3 = l1
(x1 - x3) + (x4 - x3) = l2
(x1 - x4) + (x2 - x4) = l3
On double differentiating with respect to time, we will get following three constraint relations
a1+ a3 = 0 ...(i)
a1+ a4 - 2a3 = 0 ...(ii)
a1 + a2 − 2a4 = 0 ...(iii)
Solving Eqs. (i), (ii) and (iii), we get
a2= −7a1
Which is the desired relation between a1 and a2
➤ Example.3. In the above example, if two blocks have masses 1 kg and 2 kg
respectively then find their accelerations and tensions in different strings.
Solution. Pulleys 3 and 4 are massless. Hence net force on them should be zero. Therefore, if we take T tension in the shortest string, then tension in other two strings will be 2T and 4T.
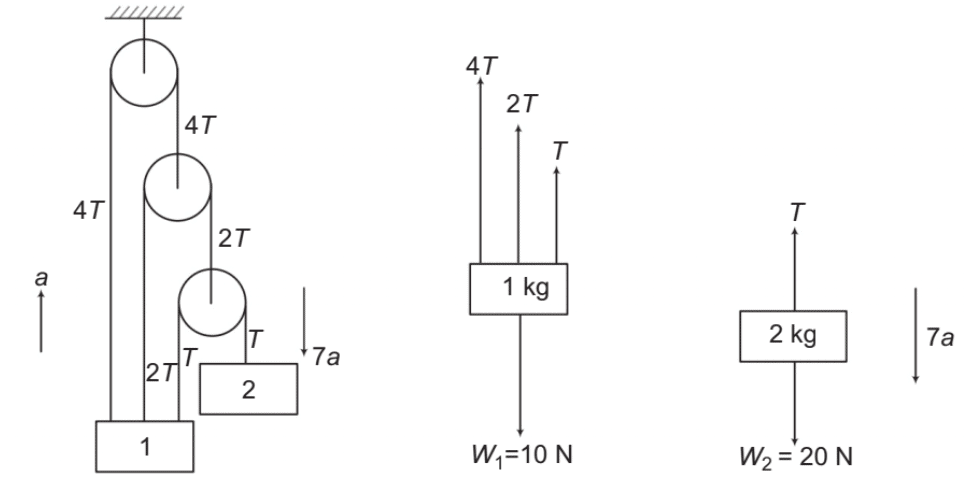
Further, if a is the acceleration of 1 in upward direction, then from the constraint equation
a2 = −7a1, acceleration of 2 will be 7a downwards.
Writing the equation, Fnet = ma for the two blocks we have
4T + 2T + T - 10 = 1 x a
7T - 10 = a ....(i)
20 - T = 2 × (7a)
20 - T = 14a ....(ii)
Solving these two equations we get,
T = 1.62 N Ans.
and a = 1.31m/s2 Ans.
Note: In a problem if ‘a’ comes out to be negative after calculations then we will change the initially assumed directions of accelerations.
➤ Example.3. Find out the velocity of block B in a pulley block system as shown in the figure.
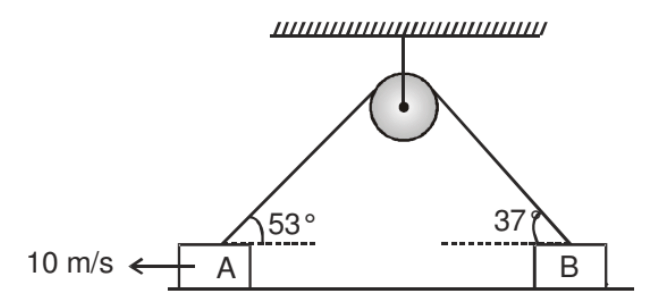
Solution. In the given pulley block system the velocity of all the particle of string is let us assume v then,
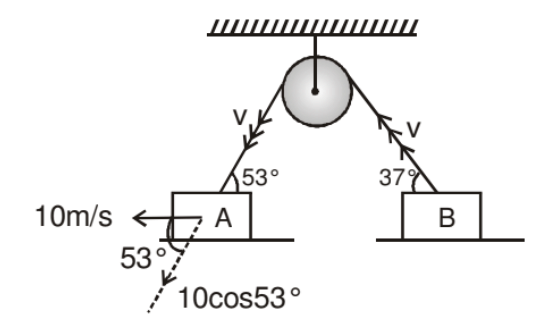
10 m/s is the real velocity of block A then its component along string is v.
⇒ 10 cos 53° = v ...(1)
If vB is the real velocity of block B then it component along string is v then
⇒ vBcos37° = v ...(2)

from (1) & (2) vB cos37° = 10 cos53°

➢ Type 2 (When Pulley is also Moving)
To understand this format we consider the following example in which pulley is moving with velocity vp and both block have velocity vA & vB respectively as shwon in figure.

If we observe the motion of A and B with respect to pulley. Then the pulley is at rest. Then from first format.
vAP = - vBP
(-ve sign indicate the direction of each block is opposite with respect to Pulley)

Note: To solve the problem put the values of vA, vB, & vP with sign.
➤ Example.1. The system shown in figure is released from rest. Find acceleration of different blocks and tension in different strings.
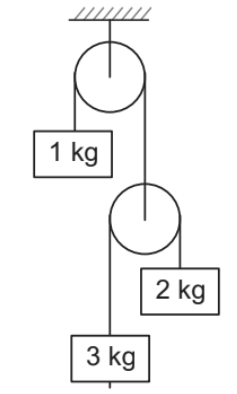
Solution.
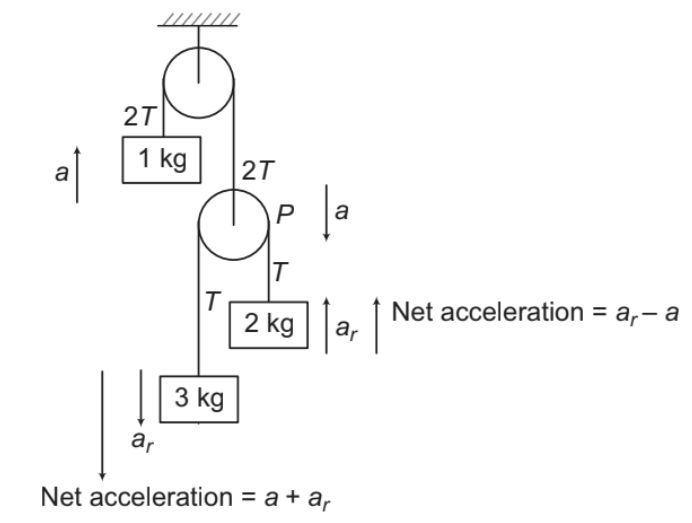
(i) Pulley P and 1 kg mass are attached with the same string. Therefore, if 1 kg mass has an acceleration ‘a’ in upward direction, then pulley P will have an acceleration ‘a’ downwards.
(ii) 2 kg and 3 kg blocks are attached with the same string passing over a moveable pulley P. Therefore their relative acceleration, ar (relative to pulley) will be same. Their net
accelerations (relative to ground) are as shown in figure.
(iii) Pulley P is massless. Hence net force on this pulley should be zero. If T is the tension in the string connecting 2 kg and 3 kg mass, then tension in the upper string will be 2T.
Now writing the equation, Fnet = for three blocks, we have:
1 kg block:
 ....(i)
....(i)
2 kg block:
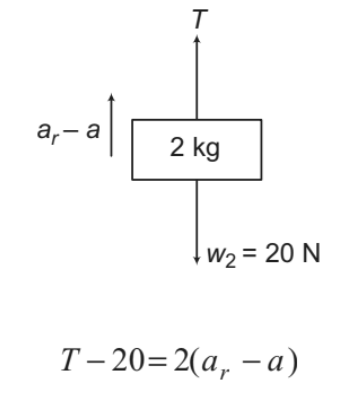 ....(ii)
....(ii)
3 kg block:
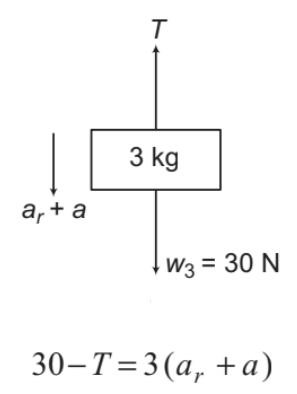 ....(iii)
....(iii)
Solving Eqs. (i), (ii) and (iii) we get,
T = 8.28 N, a = 6.55 m/s2 and ar = 0.7 m/s2
Now, acceleration of 3kg block is (a+ ar) or 7.25 m/s2 downwards and acceleration of 2kg is (ar - a )or − 5.85 m/s2 upwards. Since this comes out to be negative, hence acceleration of 2 kg block is 5.85 m/s2 downwards.
2. Wedge Constraint
Conditions:
(i) Contact must not be lost between two bodies.
(ii) Bodies are rigid.
The relative velocity/acceleration perpendicular to the contact surface of the two rigid objects is always zero. Wedge constraint is applicable for each contact.
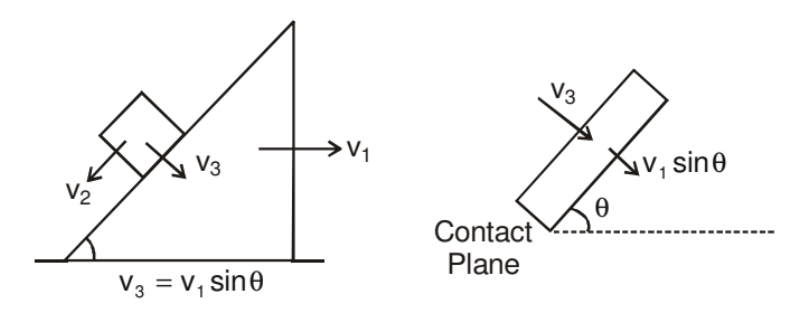
In other words,
Components of velocity and acceleration perpendicular to the contact surface of the two objects is always equal if there is no deformation and they remain in contact.
➤ Example.1. Find the relation between velocity of rod and that of the wedge at any instant in the figure shown.
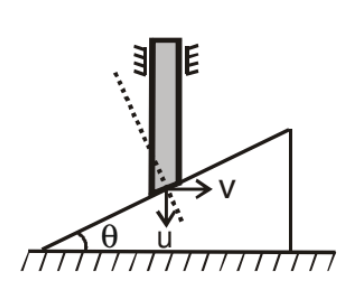
Solution. Using wedge constraint.
Component of velocity of rod along perpendicular to inclined surface is equal to velocity of wedge along that direction.
u cos θ = v sin θ
u/v = tanθ
u = v tan θ
|
289 videos|635 docs|179 tests
|
FAQs on Solved Examples: Constraint Equations - Physics for JEE Main & Advanced
| 1. What are constraint equations in mechanics? |  |
| 2. How are constraint equations used to solve problems in mechanics? |  |
| 3. Can you provide an example of a problem where constraint equations are used in mechanics? |  |
| 4. What are some common types of constraints encountered in mechanics problems? |  |
| 5. How do constraint equations help in analyzing the stability of mechanical systems? |  |

|
Explore Courses for JEE exam
|

|


















