Circular Motion | Physics Class 11 - NEET PDF Download
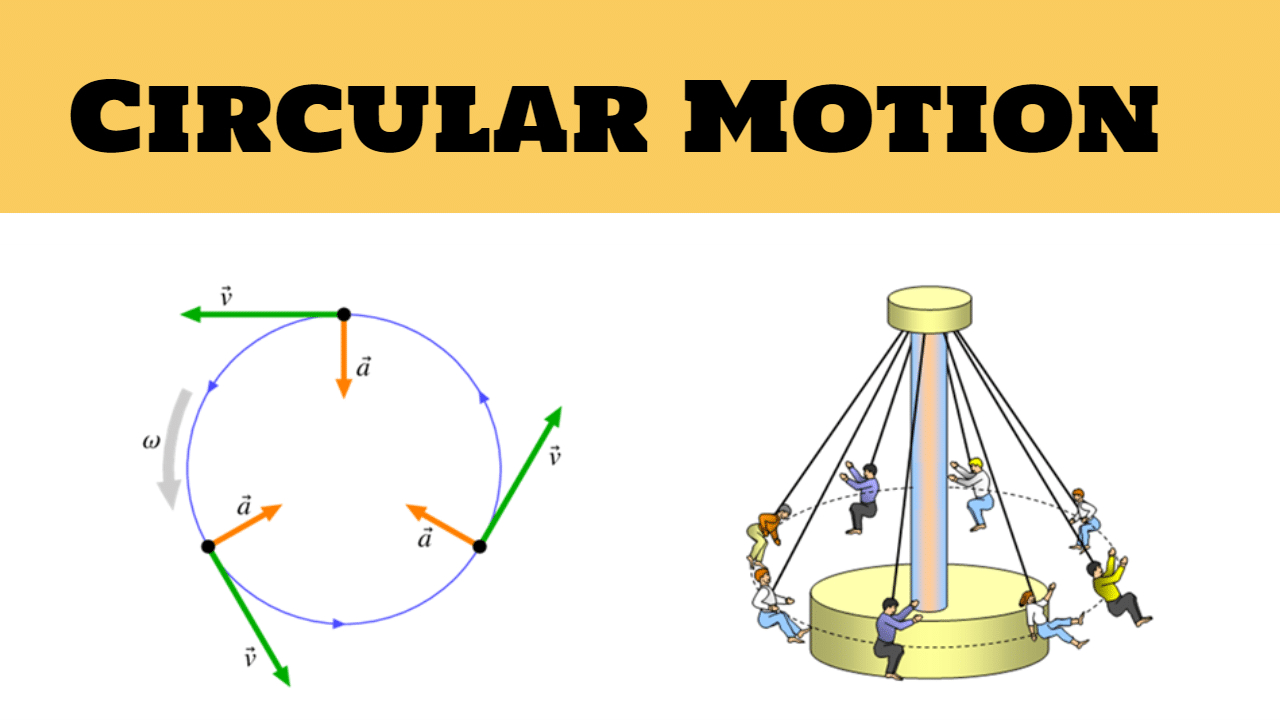
Circular Motion
- When a particle moves in a plane and keeps the same distance from a fixed or moving point, this type of movement is called circular motion.
- The fixed or moving point that the particle is measured from is known as the center.
- The distance between the fixed point and the particle is referred to as the radius.
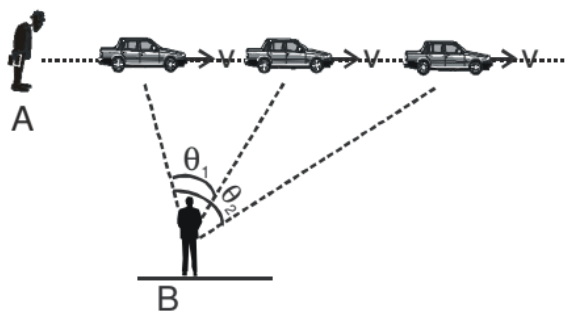
For Example: The car is moving in a straight line with respect to the man A. But the man B continuously rotate his face to see the car. So with respect to man A 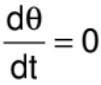 . But with respect to man B
. But with respect to man B 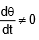 . Therefore we conclude that with respect to A the motion of car is straight line but for man B it has some angular velocity.
. Therefore we conclude that with respect to A the motion of car is straight line but for man B it has some angular velocity.
Analogy between Linear Kinematics & Circular Kinematics
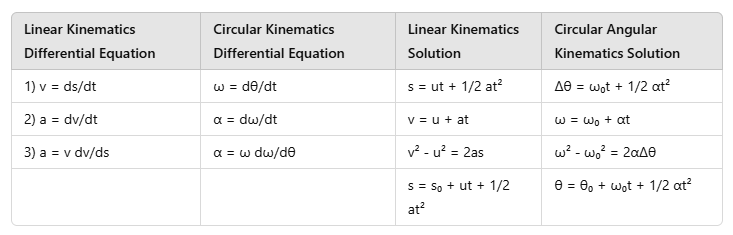
Kinematics of Circular Motion
1. Angular Position
The angle formed by the position vector with a specific reference line is known as angular position, which can be measured in either radians or degrees.
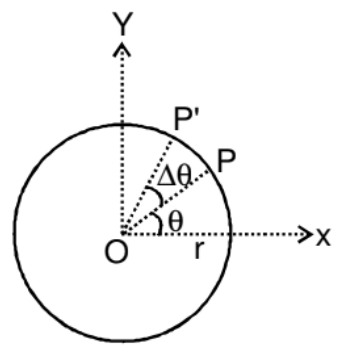
Circular motion occurs in two dimensions, or in a plane. Imagine a particle P moving in a circle with a radius r and centre O. The position of the particle P at any moment can be described by the angle θ between the line OP and the line OX. This angle θ represents the angular position of the particle. As the particle moves around the circle, its angular position θ changes. If the particle rotates through an angle Δθ in a time Δt, this describes its motion.
2. Angular Displacement
Angle rotated by a position vector of the moving particle in a given time interval with some reference line is called its angular displacement.
Important Points:
- It is a vector quantity with the SI unit of radian; other units include degrees and revolutions (2π rad = 360° = 1 rev).
- Both small and finite angular displacements are vector quantities.
- The direction of angular displacement follows the right-hand thumb rule: if your fingers point in the direction of motion, your thumb indicates the direction of angular displacement.
- Angular displacement can vary for different observers.
- It relates to angular velocity, which indicates how fast an object rotates.
- Angular displacement is essential for understanding the rotational motion of an object around a fixed axis.
3. Angular velocity ω
Angular velocity is the vector measure of the rotation rate, which refers to how fast an object rotates or revolves relative to another point.
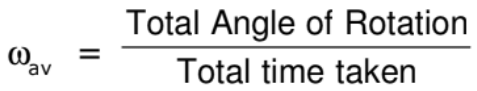
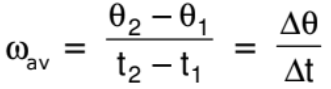
where θ1 and θ2 are angular position of the particle at time t1 and t2 respectively.
Instantaneous Angular Velocity
The rate at which the position vector of a particle with respect to the centre rotates, is called as instantaneous angular velocity with respect to the centre.
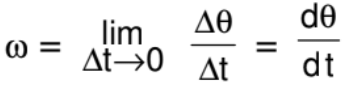
Important points:
- It is an axial vector with dimensions [T-1] and SI unit rad/s.
- For a rigid body as all points will rotate through same angle in same time, angular velocity is a characteristic of the body as a whole, e.g., angular velocity of all points of earth about its own axis is (2π/24) rad/hr.
- If a body makes `n' rotations in `t' seconds then angular velocity in radian per second will be
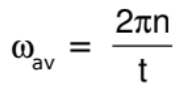
If T is the period and ‘f’ the frequency of uniform circular motion.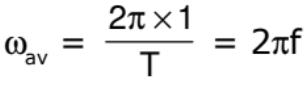
- If θ = a – bt + ct2 then ω = dθ/dt = – b + 2ct
Relation Between Speed and Angular Velocity
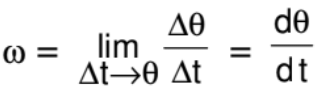
The rate of change of angular velocity is called the angular acceleration (α). Thus,

The linear distance PP' travelled by the particle in time Δt is
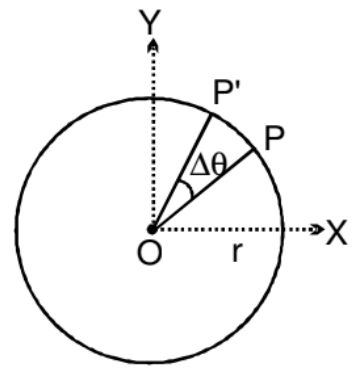

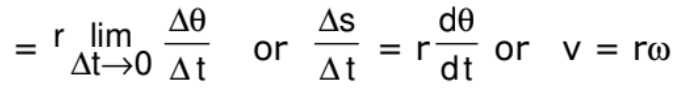
Here, v is the linear speeds of the particle. It is only valid for circular motion.
v = rω is a scalar quantity.
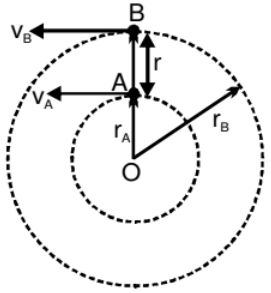
4. Relative Angular Velocity
Angular velocity is defined with respect to the point from which the position vector of the moving particle is drawn. Here angular velocity of the particle w.r.t. 'O' and 'A' will be different.
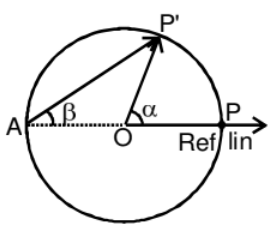
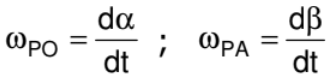
Relative angular velocity of a particle ‘A’ with respect to the other moving particle ‘B’ is the angular velocity of the position vector of ‘A’ with respect to ‘B’. That means it is the rate at which position vector of ‘A’ with respect to ‘B’ rotates at that instant
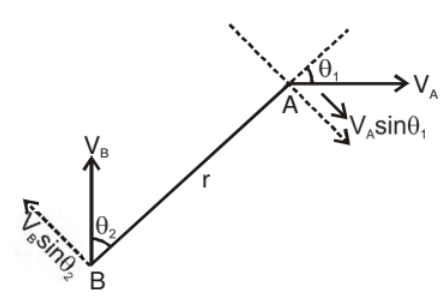

Important Points:
- If two particles are moving on the same circle or different coplanar concentric circles in same direction with different uniform angular speed ωA and ωB respectively, the rate of change of angle between OA and OB is
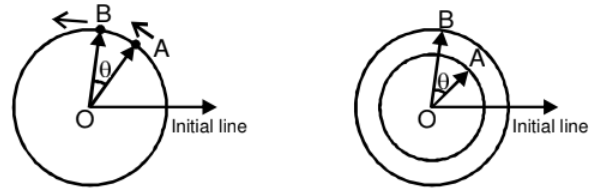
So the time taken by one to complete one revolution around O w.r.t., the other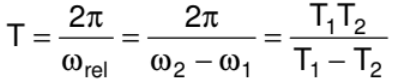
- If two particles are moving on two different concentric circles with different velocities then angular velocity of B relative to A as observed by A will depend on their positions and velocities. Consider the case when A and B are closest to each other moving in same direction as shown in figure. In this situation
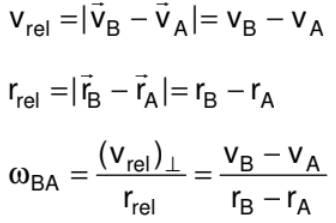
5. Angular Acceleration α
- Average Angular Acceleration
Let ω1 and ω2 be the instantaneous angular speeds at times t1 and t2 respectively, then the average angular acceleration αav is defined as
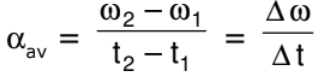
- Instantaneous Angular Acceleration
It is the limit of average angular acceleration as ∆t approaches zero, i.e.,
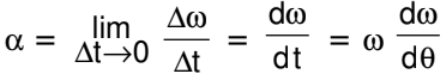
Important points:
- It is also an axial vector with dimension [T-2] and unit rad/s2
- If α = 0, circular motion is said to be uniform.
- As
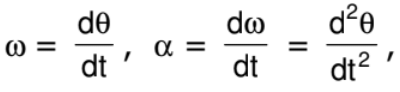
i.e., second derivative of angular displacement w.r.t time gives angular acceleration. - α is an axial vector, and its direction is the same as ω if ω increases and opposite to ω if ω decreases.
- The direction of angular acceleration is along the axis of rotation.
Types of Circular Motion
For better understanding, we can classify the circular motion in following three types:
1. Uniform circular motion in which v and ω are constant.
In this motion,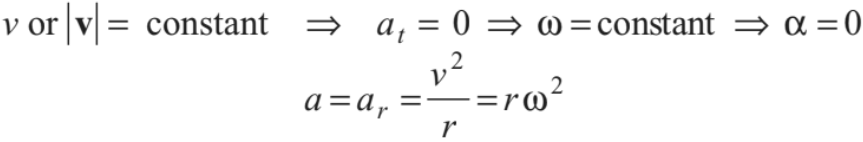
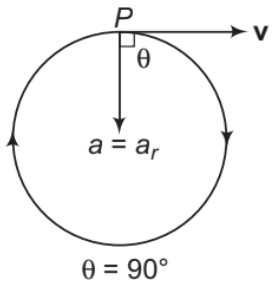
a is towards centre, v is tangential and according to the shown figure, ω is perpendicular to paper inwards or in ⊗ direction.
2. Accelerated circular motion in which v and ω are increasing. So, at is in the direction of v and α is in the direction of ω.
In the figure shown, α and ω both are perpendicular to paper inwards. Further,

and 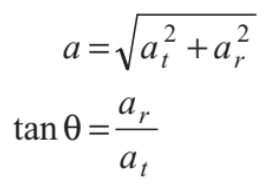
3. Retarded circular motion in which v and ω are decreasing. So, at is in the opposite direction of v and α is in the opposite direction of ω.
In the figure shown, ω is perpendicular to paper inwards in ⊗direction and α is perpendicular to paper outwards in O direction.
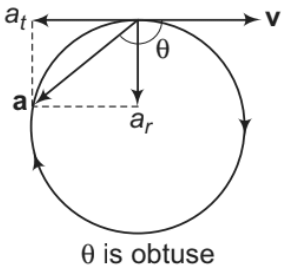
Note: In the above figures, θ is the angle between v and a.
Dynamics of Circular Motion
We know that linear acceleration of a particle in circular motion has two components, tangential and radial (or centripetal). So, normally we resolve the forces acting on the particle in two directions:
(i) Tangential
(ii) Radial
 Circular Motion
Circular Motion
In tangential direction, net force on the particle is mat and in radial direction net force is mar. In uniform circular motion, tangential acceleration is zero. Hence, net force in tangential direction is zero and in radial direction
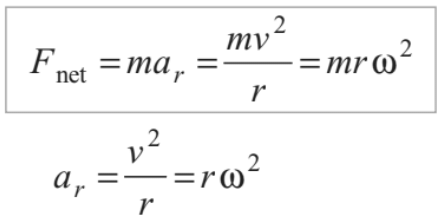
This net force (towards centre) is also called centripetal force.
In most of the cases plane of our uniform circular motion will be horizontal and one of the tangent is in vertical direction also. So, in this case we resolve the forces in:
- horizontal radial direction
- vertical tangential direction
In vertical tangential direction net force is zero (at =0) and in horizontal radial direction (towards centre) net force is mv2/r or mrω2
Note: Centripetal force mv2/r or mrω2 (towards centre) does not act on the particle but this much force is required to the particle for rotating in a circle (as it is accelerated due to change in direction of velocity). The real forces acting on the particle provide this centripetal force or we can say that vector sum of all the forces acting on the particle is equal to mv2/r or mrω2 (in case of uniform circular motion). The real forces acting on the particle may be, friction force, weight, normal reaction, tension etc.
Conical Pendulum
If a small particle of mass m tied to a string is whirled in a horizontal circle, as shown in Fig. The arrangement is called the ‘conical pendulum’. In case of conical pendulum, the vertical component of tension balances the weight in tangential direction, while its horizontal component provides the necessary centripetal force in radial direction(towards centre). Thus,
 Circular Motion in a Pendulum
Circular Motion in a Pendulum
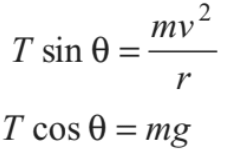
From these two equations, we can find
∴ Angular speed 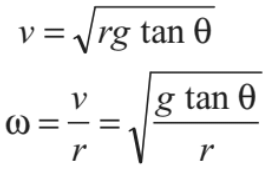
So, the time period of pendulum is
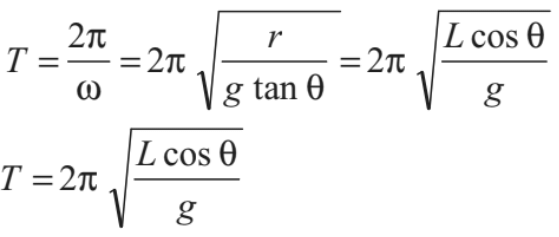 (as r = L cos θ)
(as r = L cos θ)
Motion of a Particle Inside a Smooth Cone
A particle of mass ‘m’ is rotating inside a smooth cone in horizontal circle of radius ‘r’ as shown in figure. constant speed of the particle is suppose ‘v’. Only two forces are acting on the particle in the shown directions:
(i) Normal reaction N
(ii) Weight mg
We have resolved these two forces in vertical tangential direction and horizontal radial direction. In vertical tangential direction, net force is zero.
 Motion of Particle Inside a Cone
Motion of Particle Inside a Cone
∴ N cosθ = mg
In horizontal radial direction (towards centre), net force is mv2/r
∴ 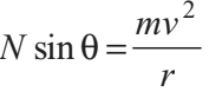
Circular Turning on Roads
When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required centripetal acceleration. If the vehicles travel in a horizontal circular path, this resultant force is also horizontal.
The necessary centripetal force is being provided to the vehicles by following three ways:
1. By Friction only
2. By Banking of Roads only
3. By Friction and Banking of Roads both.
In real life the necessary centripetal force is provided by friction and banking of roads both. Now let us write equations of motion in each of the three cases separately and see what are the constant in each case.
- By Friction Only
Suppose a car of mass m is moving at a speed v in a horizontal circular arc of radius r. In this case, the necessary centripetal force to the car will be provided by force of friction f acting towards centre
Thus, f = mv2/r
Further, limiting value of f is or μN or fL = μN = μmg (N = mg)
Therefore, for a safe turn without sliding mv2/r ≤ fL
or 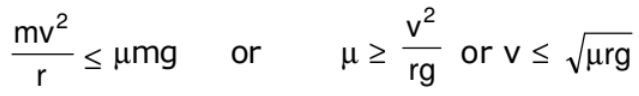
Here, two situations may arise. If m and r are known to us, the speed of the vehicle should not exceed 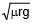 and if v and r are known to us, the coefficient of friction should be greater than
and if v and r are known to us, the coefficient of friction should be greater than 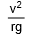 .
.
- By Banking of Roads Only
Friction is not always reliable at circular turns if high speeds and sharp turns are involved to avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is somewhat lifted compared to the inner part.
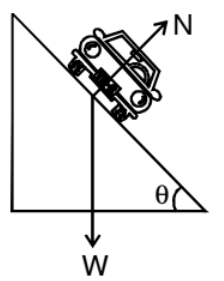
Applying Newton's second law along the radius and the first law in the vertical direction.
from these two equations, we get
- By Friction and Banking of Road Both
If a vehicle is moving on a circular road which is rough and banked also, then three forces may act on the vehicle, of these force, the first force, i.e., weight (mg) is fixed both in magnitude and direction.
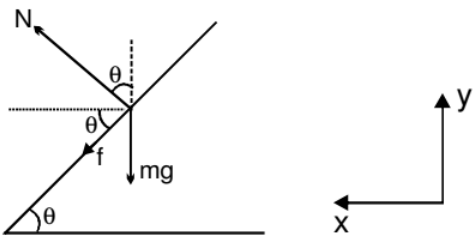
The direction of second force i.e., normal reaction N is also fixed (perpendicular or road) while the direction of the third i.e., friction f can be either inwards or outwards while its magnitude can be varied upto a maximum limit (fL = mN). So the magnitude of normal reaction N and directions plus magnitude of friction f are so adjusted that the resultant of the three forces mentioned above is mv2/r towards the center. Of these m and r are also constant. Therefore, magnitude of N and directions plus magnitude of friction mainly depends on the speed of the vehicle v. Thus, situation varies from problem to problem. Even though we can see that :
(i) Friction f will be outwards if the vehicle is at rest v = 0. Because in that case the component weight mg sinθ is balanced by f.
(ii) Friction f will be inwards if
v > 
(iii) Friction f will be outwards if
v <  and
and
(iv) Friction f will be zero if
v = 
(v) For maximum safe speed

As maximum value of friction f = μN
∴
∴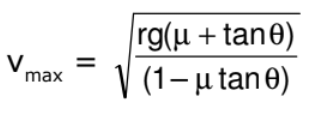
Similarly; 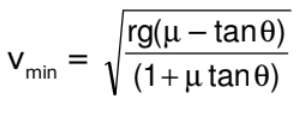
- The expression tanθ =
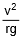 also gives the angle of banking for an aircraft, i.e., the angle through which it should tilt while negotiating a curve, to avoid deviation from the circular path.
also gives the angle of banking for an aircraft, i.e., the angle through which it should tilt while negotiating a curve, to avoid deviation from the circular path. - The expression tanθ =
 also gives the angle at which a cyclist should lean inward when rounding a corner. In this case, θ is the angle which the cyclist must make with the vertical to negotiate a safe turn.
also gives the angle at which a cyclist should lean inward when rounding a corner. In this case, θ is the angle which the cyclist must make with the vertical to negotiate a safe turn.
Death well
A motor cyclist is driving in a horizontal circle on the inner surface of vertical cylinder of radius R. Friction coefficient between tyres of motorcyclist and surface of cylinder is m. Find out the minimum velocity for which the motorcyclist can do this. v is the speed of motor cyclist and m is his mass.
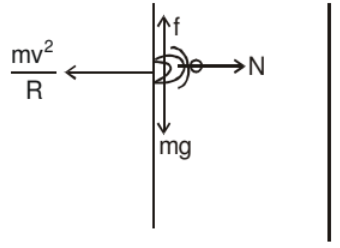
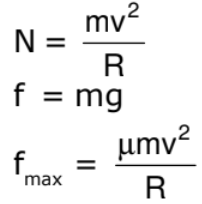
Cyclist does not drop down when
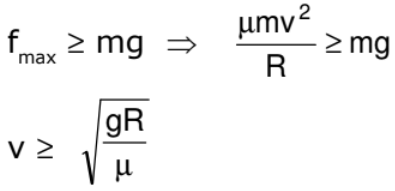
Motion of a Cyclist on a Circular Path
Suppose a cyclist is going at a speed v on a circular horizontal road of radius r which is not banked. Consider the cycle and the rider together as the system. The centre of mass C (figure shown) of the system is going in a circle with the centre at O and radius r.
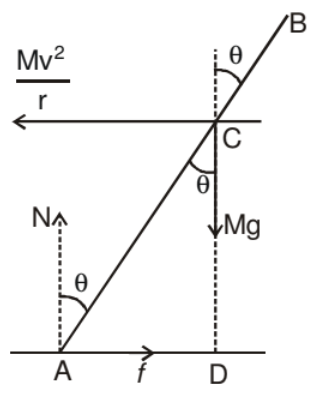
Let us choose O as the origin, OC as the X-axis and vertically upward as the Z-axis. This frame is rotating at an angular speed w = v/r about the Z-axis. In this frame the system is at rest. Since we are working from a rotating frame of reference, we will have to apply a centrifugal force on each particle. The net centrifugal force on particle will be Mω2r = Mv2/r, where M is the total mass of the system. This force will act through the centre of mass. Since the system is at rest in this frame, no other pseudo force is needed.
Figure in shows the forces. The cycle is bent at an angle θ with the vertical. The forces are
(i) weight Mg,
(ii) normal force N
(iii) friction f
(iv) Centrifugal force
In the frame considered, the system is at rest. Thus, the total external force and the total external torque must be zero. Let us consider the torques of all the forces about the point A. The torques of N and f about A are zero because these forces pass through A. The torque of Mg about A is Mg(AD) in the clockwise direction and that of Mv2/r is Mv2/r (CD) in the anticlockwise direction. For rotational equilibrium,
Mg(AD) = Mv2/r (CD)
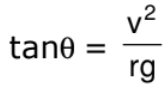
Thus, the cyclist bends at an angle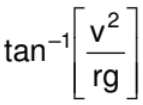 with the vertical.
with the vertical.
Centrifugal Force
When a body is rotating in a circular path and the centripetal force vanishes, the body would leave the circular path. To an observer A who is not sharing the motion along the circular path, the body appears to fly off tangentially at the point of release. To another observer B, who is sharing the motion along the circular path (i.e., the observer B is also rotating with the body which is released, it appears to B, as if it has been thrown off along the radius away from the centre by some force. This inertial force is called centrifugal force.)
Its magnitude is equal to that of the centripetal force = mv2/r . Centrifugal force is a fictitious force which has to be applied as a concept only in a rotating frame of reference to apply Newton's law of motion in that frame)
FBD of ball w.r.t non-inertial frame rotating with the ball.
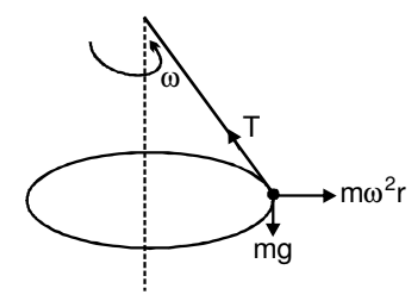
Suppose we are working from a frame of reference that is rotating at a constant, angular velocity ω with respect to an inertial frame. If we analyse the dynamics of a particle of mass m kept at a distance r from the axis of rotation, we have to assume that a force mrω2 act radially outward on the particle. Only then we can apply Newton's laws of motion in the rotating frame. This radially outward pseudo force is called the centrifugal force.
Simple Pendulum
A simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical.
The force acting on the bob are (figure)
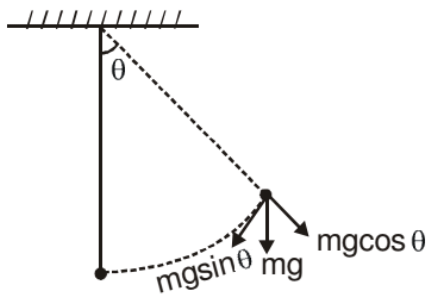
(i) Tension T
(ii) Weight mg
As the bob moves in a vertical circle with centre at O, the radial acceleration is v2/L towards O. Taking the components along this radius and applying Newton's second law, we get
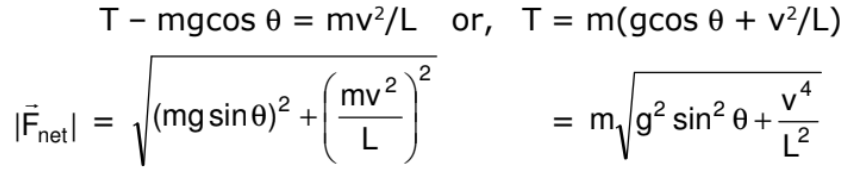
Circular Motion in Horizontal Plane
A ball of mass m attached to a light and inextensible string rotates in a horizontal circle of radius r with an angular speed w about the vertical. If we draw the force diagram of the ball.
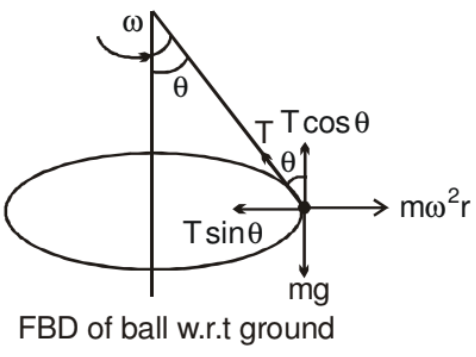
We can easily see that the component of tension force along the centre gives the centripetal force and component of tension along vertical balances the gravitation force. Such a system is called a conical pendulum.
We already know a bit about circular motion. It's a kind of movement where an object stays at the same distance from a fixed point. Circular motion is divided into two types: uniform and non-uniform. Examples include swinging a ball on a string or a car turning on a track. Now, let's talk about a special kind of circular motion called vertical circular motion.
Vertical Circular Motion
Imagine an object connected to a string and rotated around in a circle vertically.
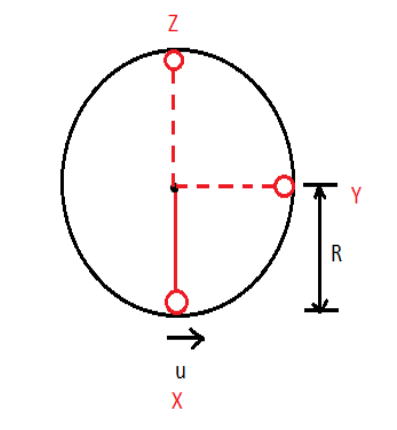 Vertical Circular Motion
Vertical Circular Motion
Between points X and Y, the tension in the string balances the weight, keeping it taut. To find the velocity needed to reach Y, we use conservation of mechanical energy.
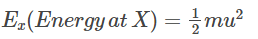
Since the particle just reaches Y, its velocity at Y is zero.
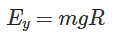
By equating the initial and final energy, we determine the velocity.
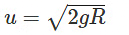
Now, if we want to find the minimum velocity to reach Z, assuming zero velocity at Z is incorrect. Velocity at Z should be such that weight equals centripetal force, making tension zero.
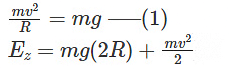
Substituting the velocity value,
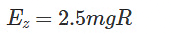
Now we equate energies for X and Z.
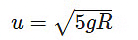
The critical values lead to three cases:
- The ball oscillates and never reaches Y.
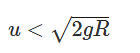
- The ball loses contact between Y and Z, starting projectile motion.
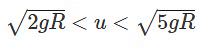
- The string never becomes slack, completing the circle.
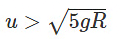
This situation is similar for a ball tied to a rod moving in a vertical circle. The only difference is that the velocity at the top can be zero, as the normal reaction of the rod balances the weight.
Solving similarly yields three cases for a rod:
- The body oscillates and doesn't reach Y.
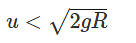
- The ball oscillates, crosses Y, but doesn't reach Z.
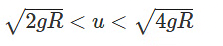
- The body completes the circle.
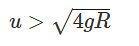
Solved Examples on Vertical Circular Motion
Q1. A particle travels in a circle of radius 20 cm at a speed that uniformly increases. If the speed changes from 5·0 m/s to 6·0 m/s in 2·0 s, find the angular acceleration.
Sol: The tangential acceleration is given by
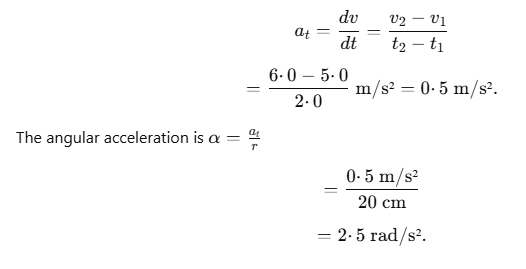
Q2. A small block of mass 100 g moves with uniform speed in a horizontal circular groove, with vertical side walls, of radius 25 cm. If the block takes 2·0 s to complete one round, find the normal contact force by the side wall of the groove.
Sol: The speed of the block is
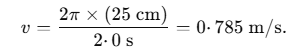
The acceleration of the block is
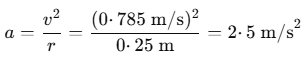
towards the centre. The only force in this direction is
the normal contact force due to the side walls. Thus,
from Newton’s second law, this force is
Sol: The situation is shown in figure (7-W2). The angle θ made by the string with the vertical is given by
sinθ = r/L. .....(i)
The forces on the particle are
(a) the tension T along the string and
(b) the weight mg vertically downward.
The particle is moving in a circle with a constant speed v. Thus, the radial acceleration towards the centre has magnitude v2/r. Resolving the forces along the radial direction and applying Newton’s second law,
T sinθ = m(v2/r). ....(ii)
As there is no acceleration in vertical direction, we have from Newton’s first law,
Tcosθ=mg.
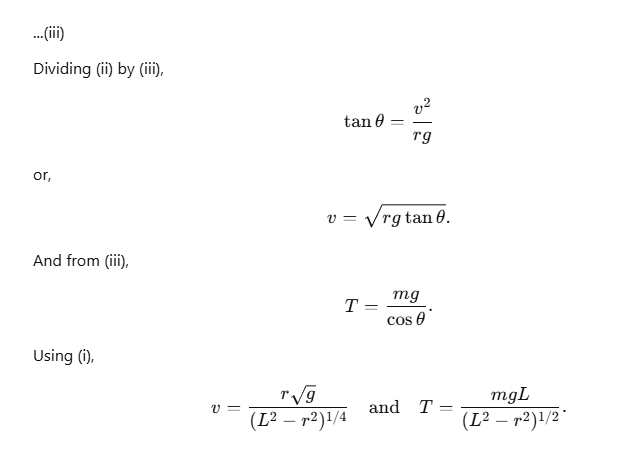
|
96 videos|367 docs|98 tests
|
FAQs on Circular Motion - Physics Class 11 - NEET
| 1. What is the difference between linear kinematics and circular kinematics? |  |
| 2. What are the types of circular motion? |  |
| 3. How does a conical pendulum work? |  |
| 4. What is the effect of circular turning on roads for vehicles? |  |
| 5. What happens in a death well in terms of circular motion? |  |






















