Second & Third Law of Thermodynamics | Physical Chemistry for NEET PDF Download
Second Law Of Thermodynamics
The second law of thermodynamics put restrictions upon the direction of heat transfer and achievable efficiencies of heat engines. The first law of thermodynamics states that the energy of the universe remains constant, though energy can be exchanged between system and surroundings, it can’t be created or destroyed.
While the first law of thermodynamics gives information about the quantity of energy transfer is a process, it fails to provide any insights about the direction of energy transfer and the quality of the energy. The first law cannot indicate whether a metallic bar of uniform temperature can spontaneously become warmer at one end and cooler at others. All that the law can state is that there will always be energy balance if the process occurs.
It is the second law of thermodynamics that provides the criterion for the feasibility of any process. A process cannot occur unless it satisfies both the first and second laws of thermodynamics.
What is the Second Law of Thermodynamics?
The second law of thermodynamics states that any spontaneously occurring process will always lead to an escalation in the entropy (S) of the universe. In simple words, the law explains that an isolated system’s entropy will never decrease over time.
Nonetheless, in some cases where the system is in thermodynamic equilibrium or going through a reversible process, the total entropy of a system and its surroundings remains constant. The second law is also known as the Law of Increased Entropy.
Second Law of Thermodynamics Equation
Mathematically, the second law of thermodynamics is represented as;
ΔSuniv > 0
where ΔSuniv is the change in the entropy of the universe.
Entropy is a measure of the randomness of the system or it is the measure of energy or chaos within an isolated system. It can be considered as a quantitative index that describes the quality of energy.
Meanwhile, there are few factors that cause an increase in entropy of the closed system. Firstly, in a closed system, while the mass remains constant there is an exchange of heat with the surroundings. This change in the heat content creates a disturbance in the system thereby increasing the entropy of the system.
Secondly, internal changes may occur in the movements of the molecules of the system. This leads to disturbances which further causes irreversibilities inside the system resulting in the increment of its entropy.
Different Statements of The Law
here are two statements on the second law of thermodynamics which are;
- Kelvin- Plank Statement
- Clausius Statement
- Kelvin-Planck Statement
It is impossible for a heat engine to produce a network in a complete cycle if it exchanges heat only with bodies at a single fixed temperature.
Exceptions:
If Q2 = 0 (i.e., Wnet = Q1, or efficiency = 1.00), the heat engine produces work in a complete cycle by exchanging heat with only one reservoir, thus violating the Kelvin-Planck statement. - Clausius’s Statement
It is impossible to construct a device operating in a cycle that can transfer heat from a colder body to warmer without consuming any work. In other words, unless the compressor is driven by an external source, the refrigerator won’t be able to operate. Heat pump and Refrigerator works on Clausius’s statement.
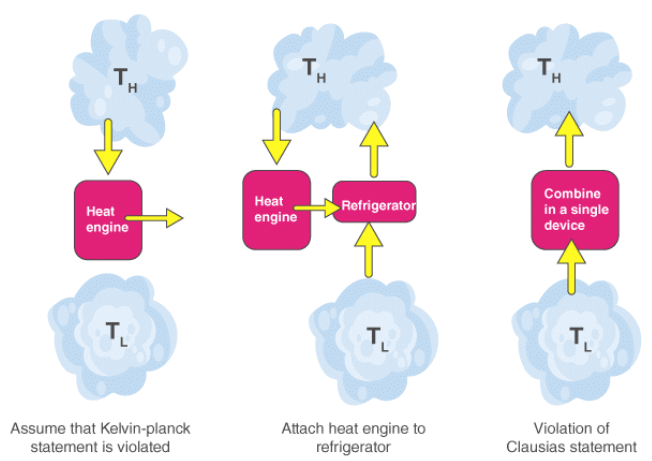
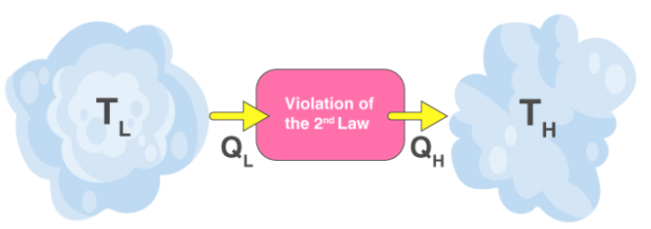 Both Clausius’s and Kelvin’s statements are equivalent i.e a device violating Clausius’s statement will also violate Kelvin’s statement and vice versa.
Both Clausius’s and Kelvin’s statements are equivalent i.e a device violating Clausius’s statement will also violate Kelvin’s statement and vice versa.
 In addition to these statements, a French physicist named Nicolas Léonard Sadi Carnot also known as”father of thermodynamics,” basically introduced the Second Law of Thermodynamics. However, as per his statement, he emphasized the use of caloric theory for the description of the law. Caloric (self repellent fluid) relates to heat and Carnot observed that some caloric was lost in the motion cycle.
In addition to these statements, a French physicist named Nicolas Léonard Sadi Carnot also known as”father of thermodynamics,” basically introduced the Second Law of Thermodynamics. However, as per his statement, he emphasized the use of caloric theory for the description of the law. Caloric (self repellent fluid) relates to heat and Carnot observed that some caloric was lost in the motion cycle.
Perpetual Motion Machine of the Second Kind (PMM2)
The device that produces work while interacting with a single heat reservoir is known as a perpetual motion machine of the second kind (PMM2). Also, a device that violates the second law of thermodynamics is a perpetual motion machine of the second kind.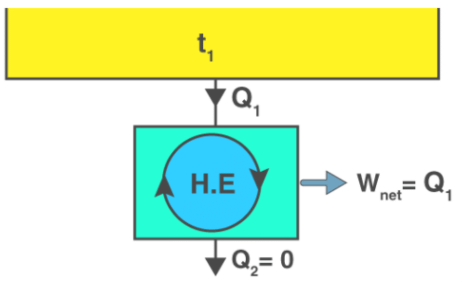 Thus, a heat engine has to interact with at least two thermal reservoirs at different temperatures to produce work in a cycle. So long as there is a difference in temperature, motive power (i.e., work) can be produced. If the bodies with which the heat engine exchange heat are of finite heat capacities, work will be produced by the heat engine until the temperature of the two bodies is equalised.
Thus, a heat engine has to interact with at least two thermal reservoirs at different temperatures to produce work in a cycle. So long as there is a difference in temperature, motive power (i.e., work) can be produced. If the bodies with which the heat engine exchange heat are of finite heat capacities, work will be produced by the heat engine until the temperature of the two bodies is equalised.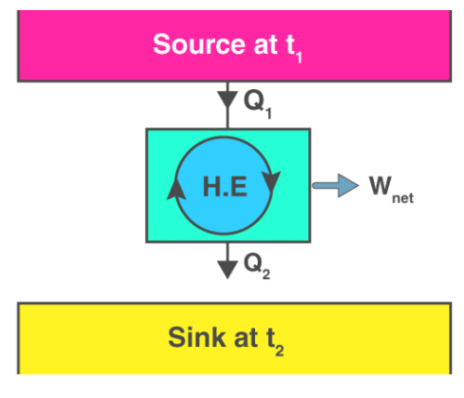
Solved Examples of Second Law Of Thermodynamics
Example 1: A heat pump uses 300 J of work to remove 400 J of heat from the low-temperature reservoir. How much heat is delivered to a higher temperature reservoir?
Solution: W = 300 J
QC = 400 J
QH = W + QC
QH = 300 J + 400 J
QH = 700 J
Heat delivered to the higher temperature reservoir is 700 J.
Example 2: A reversible heat engine receives 4000 KJ of heat from a constant temperature source at 600 K. If the surrounding is at 300K then determine (a) the availability of heat energy (b) unavailable heat.
Solution: Q1 = 4000 KJ
T1 = 600K
T0 = 300 K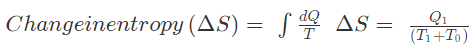
Change in entropy = 4.44 KJ/K
The availability of heat energy,
A = Q1 – T0(ΔS)
A = 4000 – 300(4.44)
A = 2,668 KJ.
Unavailable heat (U.A) = T0 (ΔS)
(U.A) = 300 (4.44)
(U.A) = 1332 KJ.
(a) the availability of heat energy (A) = 2668 KJ
(b) Unavailable heat (U.A) = 1332 KJ.
Third Law Of Thermodynamics
The third law of thermodynamics states that the entropy of a perfect crystal at a temperature of zero Kelvin (absolute zero) is equal to zero.
Entropy, denoted by ‘S’, is a measure of the disorder/randomness in a closed system. It is directly related to the number of microstates (a fixed microscopic state that can be occupied by a system) accessible by the system, i.e. the greater the number of microstates the closed system can occupy, the greater its entropy. The microstate in which the energy of the system is at its minimum is called the ground state of the system.
At a temperature of zero Kelvin, the following phenomena can be observed in a closed system:
- The system does not contain any heat.
- All the atoms and molecules in the system are at their lowest energy points.
Therefore, a system at absolute zero has only one accessible microstate – it’s ground state. As per the third law of thermodynamics, the entropy of such a system is exactly zero.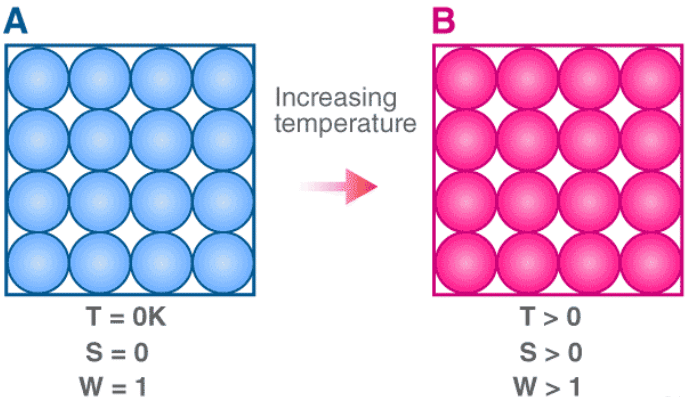 This law was developed by the German chemist Walther Nernst between the years 1906 and 1912.
This law was developed by the German chemist Walther Nernst between the years 1906 and 1912.
Alternate Statements of the 3rd Law of Thermodynamics
The Nernst statement of the third law of thermodynamics implies that it is not possible for a process to bring the entropy of a given system to zero in a finite number of operations.
The American physical chemists Merle Randall and Gilbert Lewis stated this law differently: when the entropy of each and every element (in their perfectly crystalline states) is taken as 0 at absolute zero temperature, the entropy of every substance must have a positive, finite value. However, the entropy at absolute zero can be equal to zero, as is the case when a perfect crystal is considered.
The Nernst-Simon statement of the 3rd law of thermodynamics can be written as: for a condensed system undergoing an isothermal process that is reversible in nature, the associated entropy change approaches zero as the associated temperature approaches zero.
Another implication of the third law of thermodynamics is: the exchange of energy between two thermodynamic systems (whose composite constitutes an isolated system) is bounded.
Why is it Impossible to Achieve a Temperature of Zero Kelvin?
For an isentropic process that reduces the temperature of some substance by modifying some parameter X to bring about a change from ‘X2’ to ‘X1’, an infinite number of steps must be performed in order to cool the substance to zero Kelvin.
This is because the third law of thermodynamics states that the entropy change at absolute zero temperatures is zero. The entropy v/s temperature graph for any isentropic process attempting to cool a substance to absolute zero is illustrated below.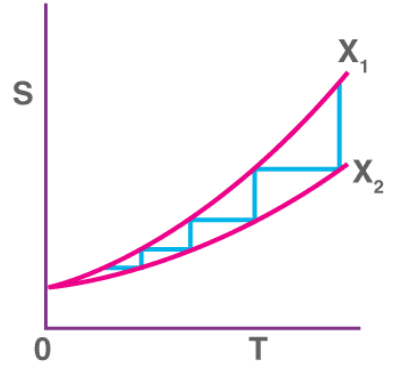 From the graph, it can be observed that – the lower the temperature associated with the substance, the greater the number of steps required to cool the substance further. As the temperature approaches zero kelvin, the number of steps required to cool the substance further approaches infinity.
From the graph, it can be observed that – the lower the temperature associated with the substance, the greater the number of steps required to cool the substance further. As the temperature approaches zero kelvin, the number of steps required to cool the substance further approaches infinity.
Mathematical Explanation of the Third Law
As per statistical mechanics, the entropy of a system can be expressed via the following equation:
S – S0 = 𝑘B ln𝛀
Where,
- S is the entropy of the system.
- S0 is the initial entropy.
- 𝑘B denotes the Boltzmann constant.
- 𝛀 refers to the total number of microstates that are consistent with the system’s macroscopic configuration.
Now, for a perfect crystal that has exactly one unique ground state, 𝛀 = 1. Therefore, the equation can be rewritten as follows:
S – S0 = 𝑘B ln(1) = 0 [because ln(1) = 0]
When the initial entropy of the system is selected as zero, the following value of ‘S’ can be obtained:
S – 0 = 0 ⇒ S = 0
Thus, the entropy of a perfect crystal at absolute zero is zero.
Applications of the Third Law of Thermodynamics
An important application of the third law of thermodynamics is that it helps in the calculation of the absolute entropy of a substance at any temperature ‘T’. These determinations are based on the heat capacity measurements of the substance. For any solid, let S0 be the entropy at 0 K and S be the entropy at T K, then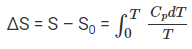
According to the third law of thermodynamics, S0 = 0 at 0 K,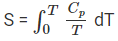
The value of this integral can be obtained by plotting the graph of Cp / T versus T and then finding the area of this curve from 0 to T. The simplified expression for the absolute entropy of a solid at temperature T is as follows: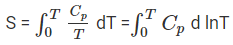
= Cp ln T = 2.303 Cp log T
Here Cp is the heat capacity of the substance at constant pressure and this value is assumed to be constant in the range of 0 to T K.
|
117 videos|226 docs|237 tests
|
FAQs on Second & Third Law of Thermodynamics - Physical Chemistry for NEET
| 1. What is the second law of thermodynamics? |  |
| 2. What is the third law of thermodynamics? |  |
| 3. How does the second law of thermodynamics relate to energy efficiency? |  |
| 4. Why is the third law of thermodynamics important in understanding absolute zero? |  |
| 5. How do the second and third laws of thermodynamics impact everyday life? |  |
















