Integrals of Some Functions | Mathematics (Maths) Class 12 - JEE PDF Download
Introduction
Consider the integral  dx
dx
If we change the variable from x to θ by the substitution x = a sinθ, then the identity
1 – sin2θ = cos2θ
allows us to get rid of the roots sign because
 Notice the difference between the substitution u = a2 – x2 (in which the new variable is a function of the old one) are the substitution x = a sin θ (the old variable is a function of the new one).
Notice the difference between the substitution u = a2 – x2 (in which the new variable is a function of the old one) are the substitution x = a sin θ (the old variable is a function of the new one).
In general, we can make a substitution of the form x = g(t) by using the Substitution Rule in reverse. To make our calculations simpler, we assume that g has an inverse function; that is, g is one-to-one.
This kind of substitution is called inverse substitution.
We can make the inverse substitution x = a sin θ provided that it defines a one-to-one function. This can be accomplished by restricting θ to lie in the interval [–π/2, π/2].
Some Standard Integrals









Solved Examples
Ex.1 Evaluate  where a > 0
where a > 0
Sol.
We let x = a secθ, where 0 < θ < π/2 or π < θ < 3π/2. Then dx = a sec θ tan θ dθ and









Ex.2 Integrate 
Sol.





Ex.3 Integrate (3x + 1) / (2x2 – 2x + 3).
Sol. Here (d/dx) (2x2 – 2x + 3) = 4x – 2.






Ex.4 Integrate 
Sol.





Ex.5 Evaluate  dx.
dx.
Sol.




Integration of Irrational Functions
Certain types of integrals of algebraic irrational expressions can be reduced to integrals of rational functions by a appropriate change of the variable. Such transformation of an integral is called its rationalization.
- If the integrand is a rational function of fractional powers of an independent variable x, i.e. the function R
 then the integral can be rationalized by the substitution x = tm, where m is the least common multiple of the numbers q1, q2, ...., qk.
then the integral can be rationalized by the substitution x = tm, where m is the least common multiple of the numbers q1, q2, ...., qk. - If the integrand is a rational function of x and fractional powers of a linear fractional function of the form
 then rationalization of the integral is effected by the substitution
then rationalization of the integral is effected by the substitution  where m has the same sense as above.
where m has the same sense as above.
Solved Examples
Ex.1 Evaluate 
Sol.
Rationalizing the denominator, we have 



Ex.2 Evaluate I = 
Sol. The least common multiple of the numbers 3 and 6 is 6, therefore we make the substitution
x = t6, dx = 6t5 dt.


Ex.3 Evaluate I = 
Sol. The integrand is a rational function of  therefore we put 2x – 3 = t6, whence
therefore we put 2x – 3 = t6, whence


Returning to x, we get
Ex.4 Evaluate 
Sol.
Let x = t3 ⇒ dx = 3t2 then




Ex.5 Evaluate I = 
Sol. The integrand is a rational function of x and the expression  therefore let us introduce the substitution
therefore let us introduce the substitution




Integrals of the type  where x & y are linear or quadratic expressions
where x & y are linear or quadratic expressions
Ex.1 Integrate 
Sol.
Put 4x + 3 = t2, so that 4dx = 2tdt and (2x + 1) 


Ex.2 Evaluate 
Sol.
Put (x + 2) = t2, so that dx = 2t dt, Also x = t2 – 2.
∴ 
 dividing the numerator by the denominator
dividing the numerator by the denominator


Ex.3 Integrate 
Sol.
Put (x + 1) = t2, so that dx = 2t dt. Also x = t2 – 1.






Ex.4 Integrate 
Sol.
Put (1 + x) = 1/t, so that dx = – (1/t2) dx.
Also x = (1/t) – 1.




Ex.5 Evaluate 
Sol.
Put x = 1/t, so that dx = – (1/t2) dt.
∴ 

Now put 1 + t2 = z2 so that t dt = z dz. Then


 [∵ t = 1/x]
[∵ t = 1/x]
Integration Of A Binomial Differential
The integral  where m, n, p are rational numbers, is expressed through elementary functions only in the following three cases :
where m, n, p are rational numbers, is expressed through elementary functions only in the following three cases :
Case I : p is an integer. Then, if p > 0, the integrand is expanded by the formula of the binomial; but if p < 0, then we put x = tk, where k is the common denominator of the fractions and n.
Case II : is an integer. We put a + bxn = tα, where α is the denominator of the fraction p.
is an integer. We put a + bxn = tα, where α is the denominator of the fraction p.
Case III : + p is an integer we put a + bxn = tαxn, where a is the denominator of the fraction p.
+ p is an integer we put a + bxn = tαxn, where a is the denominator of the fraction p.
Ex.1 Evaluate I = 
Sol.
 Here p = 2, i.e. an integer, hence we have case I.
Here p = 2, i.e. an integer, hence we have case I.


Ex.2 Evaluate I = 
Sol. 


i.e. an integer.we have case II. Let us make the substitution. Hence , 
Ex.3 Evaluate I = 
Sol.
Here p = – 1/2 is a fraction, m+1/2 = -5/2 also a fraction, but m+1/n + p/2 = -5/2 -1/2 = -3 is an integer, i.e. we have case III, we put 1 + x4 = x4/2,
Hence 
Substituting these expression into the integral, we obtain


Returning to x, we get I = 
Integration by Substitution
Let g be a function whose range is an interval l, and let f be a function that is continuous on l. If g is differentiable on its domain and F is an antiderivative of f on l, then  f(g(x))g'(x) dx = F(g(x)) + C.
f(g(x))g'(x) dx = F(g(x)) + C.
If u = g(x), then du = g'(x) and  f(u) du = F(u) + C .
f(u) du = F(u) + C .
Guidelines for making a change of variable
1. Choose a substitution u = g(x). Usually, it is best to choose the inner part of a composite function, such as a quantity raised to a power.
2. Compute du = g'(x) dx.
3. Rewrite the integral in terms of the variable u.
4. Evaluate the resulting integral in terms of u.
5. Replace u by g(x) to obtain an antiderivative in terms of x.
The General Poser Rule for Integration
If g is a differentiable function of x, then 
Rationalizing Substitutions
Some irrational functions can be changed into rational functions by means of appropriate substitutions.
In particular, when an integrand contains an expression of the form  then the substitution u =
then the substitution u =  may be effective.
may be effective.
Some Standard Substitutions
Integration Using Trigonometric Identities
In the integration of a function, if the integrand involves any kind of trigonometric function, then we use trigonometric identities to simplify the function that can be easily integrated.
Few of the trigonometric identities are as follows:
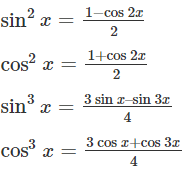
All these identities simplify integrand, that can be easily found out.
Solved Examples:
Ex.1 Evaluate  (x2 +1)2 (2x) dx .
(x2 +1)2 (2x) dx .
Sol. Letting g(x) = x2 + 1, we obtain g'(x) = 2x and f(g(x)) = [g(x)]2.
From this, we can recognize that the integrand and follows the f(g(x)) g'(x) pattern. Thus, we can write 
Ex.2 Evaluate 
Sol. 
Ex.3 Evaluate 
Sol.
Let u = x4 + 2 ⇒ du = 4x3 dx


Ex.4 Evaluate 
Sol.
Let u = x3 – 2. Then du = 3x2 dx. so by substitution :


Ex.5 Evaluate 
Sol. Let u =  . Then u2 = x + 4, so x = u2 –4 and dx = 2u du.
. Then u2 = x + 4, so x = u2 –4 and dx = 2u du.
Therefore 



Integration by Parts:
 dx where u & v are differentiable functions.
dx where u & v are differentiable functions.
Note : While using integration by parts, choose u & v such that
(a)  dx v is simple &
dx v is simple &
(b)  dx is simple to integrate.
dx is simple to integrate.
This is generally obtained, by keeping the order of u & v as per the order of the letter in ILATE, where
I – Inverse function
L – Logarithmic function
A – Algebraic function
T – Trigonometric function
E – Exponential function
Remember This:
Proof:
Integrating by parts taking sin bx as the second function,

Again integrating by parts taking cos bx as the second function, we get


Transposing the term -a2/b2 I to the left hand side, we get 





Solved Examples
Ex.1 Integrate xn log x
Sol.




Ex.2 Evaluate  dx
dx
Sol.
Put sec–1 x = t so that 
Then the given integral = 

= t (log t – log e) + c = sec–1 x (log (sec–1 x) – 1) + c 
Ex.3 Evaluate  dx.
dx.
Sol.
Put x = cos θ so that dx = - sin θ dθ. the given integral





Ex.4 Evaluate 
Sol.
We have 
 [ x3 = x(x2 + 1) - x]
[ x3 = x(x2 + 1) - x]
integrating by parts taking x2 as the second function


Ex.5 Evaluate  dx.
dx.
Sol.

 (put, 2x + 2 = 3 tanθ ⇒ 2 dx = 3 sec2θ dθ )
(put, 2x + 2 = 3 tanθ ⇒ 2 dx = 3 sec2θ dθ )


Integration by Partial Fractions
We know that a Rational Number can be expressed in the form of p/q, where p and q are integers and q≠0. Similarly, a rational function is defined as the ratio of two polynomials which can be expressed in the form of partial fractions: P(x)/Q(x), where Q(x)≠0.
- Proper partial fraction: When the degree of the numerator is less than the degree of the denominator, then the partial fraction is known as a proper partial fraction.
- Improper partial fraction: When the degree of the numerator is greater than the degree of denominator then the partial fraction is known as an improper partial fraction. Thus, the fraction can be simplified into simpler partial fractions, that can be easily integrated.
In this section, we show how to integer any rational function (a ratio of polynomials) by expressing it as a sum of simpler fractions, called partial fractions, that we already know how to integrate. To illustrate the method, observe that by taking the fractions 2/(x – 1) and 1/(x + 2) to a common denominator we obtain

If we now reverse the procedure, we see how to integrate the function on the right side of this equation 
To see how the method of partial fractions works in general, let's consider a rational function 
Where P and Q are polynomials. It's possible to express f as sum of simpler fractions provided that the degree of P is less than the degree of Q. Such a rational function is called proper. Recall that if P(x) = 
where an ≠ 0, then the degree of P is n and we write deg (P) = n.
If f is improper, that is, deg(P)  deg (Q), then we must take the preliminary step of dividing Q into P (by division) until a remainder R(x) is obtained such that deg (R) < deg(Q). The division statement is
deg (Q), then we must take the preliminary step of dividing Q into P (by division) until a remainder R(x) is obtained such that deg (R) < deg(Q). The division statement is
 where S and R are also polynomials. As the following example illustrates, sometimes this preliminary step is all that is required.
where S and R are also polynomials. As the following example illustrates, sometimes this preliminary step is all that is required.
Solved Examples:
Ex.1 Evaluate
 dx.
dx.Sol. Since the degree of the numerator is greater than the degree of the denominator, we first perform the long division. This enables us to write

The next step is to factor the denominator Q(x) as far as possible . It can be shown that any polynomial Q can be factored as a product of linear factors (of the form ax + b) and irreducible quadratic factors
(of the form ax2 + bx + c, where b2 – 4ac < 0).
For instance, if Q(x) = x4 – 16, we could factor it as Q(x) = (x2 – 4) (x2 + 4) = (x – 2) (x + 2) (x2 + 4)
The third step is to express the proper rational function R(x)/Q(x) (from equation 1) as a sum of partial fractions of the form

A theorem in algebra guarantees that it is always possible to do this. We explain the details for the four cases that occur.
Case I : The Denominator Q(x) is a product of distinct linear factors.
This means that we can write Q(x) = (a1x + b1) (a2x + b2) ... (akx + bk)
where no factor is repeated (and no factor is a constant multiple of another). In this case the partial fraction theorem states that there exist constants A1,A2,...,Ak such that.
These constants can be determined as in the following example.
Ex.2 Evaluate  dx.
dx.
Sol. Since the degree of the numerator is less than the degree of the denominator, we don't need to divide.
We factor the denominator as 2x3 + 3x2 – 2x = x(2x2 + 3x – 2) = x(2x – 1) (x + 2)
Since the denominator has three distinct linear factors, the partial fraction decomposition of the integrand (2) has the form.

To denominator the values of A, B and C, we multiply both sides of this equation by the product of the denominators, x(2x – 1) (x + 2), obtaining.
(4) x2 + 2x – 1 = A(2x – 1) (x + 2) + Bx(x + 2) + Cx(2x – 1)
Expanding the right side of equation 4 and writing it in the standard form for polynomials, we get
(5) x2 + 2x – 1 = (2A + B + 2C) x2 + (3A + 2B – C) x – 2A
The polynomials in Equation 5 are identical, so their coefficients must be equal. The coefficient of x2 on the right side, 2A + B + 2C, must equal the coefficient of x2 on the left side-namely, 1. Likewise. The coefficients of x are equal and the constant terms are equal. This gives the following system of equation for A, B and C.
2A + B + 2C = 1 , 3A + 2B – C = 2 , – 2A = –1
Solving, we get 


In integrating the middle term we have made the mental substitution u = 2x – 1, which gives du = 2dx and dx = du/2.
Case II : Q(x) is a product of linear factors, some of which are repeated
Suppose the first linear factor (a1x + b1) is repeated r times, that is, (a1x + b1)r occurs in the factorization of Q(x). Then instead of the single term A1/(a1x + b1) in equation 2, we would use(6) 
By way of illustration, we could write 
but we prefer to work out in detail a simpler example.
Ex.3 Evaluate  dx
dx
Sol.
The first step is to divide. The result of long division is 
The second step is to factor the denominator Q(x) = x3 – x2 – x + 1. Since Q(1) = 0, we know that x – 1 is a factor and we obtain x3 – x2 – x + 1 = (x – 1) (x2 – 1) = (x – 1) (x – 1)(x + 1) = (x – 1)2 (x + 1) Since the linear factor x – 1 occurs twice, the partial fraction decompositoin is

Multiplying by the least common denominator (x – 1)2 (x + 1), we get
(7) 4x = A(x – 1)(x + 1) + B(x + 1) + C(x – 1)2 = (A + C) x2 + (B – 2x) x + (–A + B + C)
Now we equate coefficients : A + C = 0,B – 2C = 4, –A + B + C = 0
Solving, we obtain A = 1, B = 2, and C = – 1, so




Case III : Q(x) contains irreducible quadratic factors, none of which is repeated
If Q(x) has the factor ax2 + bx + c, where b2 – 4ac < 0, then in addition to the partial fractions in equation 2 and 6, the expression or R(x)/Q(x) will have a term of the form.(8)  where A and B are constants to be determined. For instance, the function givenby f(x) = x/[(x – 2)(x2 + 1) (x2 + 4)] has a partial fraction decomposition of the form
where A and B are constants to be determined. For instance, the function givenby f(x) = x/[(x – 2)(x2 + 1) (x2 + 4)] has a partial fraction decomposition of the form

The term given in (8) can be integrated by completing the square and using the formula.

Ex.4 Evaluate  dx
dx
Sol.
Since x3 + 4x = x(x2 + 4) can't be factored further, we write 
Multiplying by x(x2 + 4), we have 2x2 – x + 4 = A (x2 + 4) + (Bx + C) x = (A + B) x2 + Cx + 4A Equating coefficients, we obtain A + B =2 C = –1 4A = 4
Thus A = 1, B = 1 and C = –1 and 
In order to integrate the second term we split it into to parts 
We make the substitution u = x2 + 4 in the first of these integrals so that du = 2x dx. We evaluate the second integral by means of Formula 9 with a = 2.


Case IV : Q(x) Contains A repeated irreducible quadratic factor.
If Q (x) has the factor (ax2 + bx + c)r, where b2 – 4ac < 0, then instead of the single partial fraction
occurs in the partial fraction decomposition of R(x)/Q(x), each of the terms in (10) can be integrated by first completing the square.
Ex.5 Write out the form of the partial fraction decomposition of the function

Sol.

Ex.6 Evaluate 
Sol. The form of the partial fraction decomposition is 
Multiplying by x(x2 + 1)2, we have –x3 + 2x2 – x + 1 = A(x2 + 1)2 + (Bx + C) x (x2 + 1) + (Dx + E)x
= A(x4 + 2x2 + 1) + B(x4 + x2) + C(x3 + x) + Dx2 + Ex = (A + B) x4 + Cx3 + (2A + B + D) x2 + (C + E) x + A
If we equate coefficient, we get the system A + B = 0 ,C = –1 ,2A + B + D = 2 ,C+E =–1 , A=1
Which the solution A = 1, B = –1, D = 1, and E = 0. Thus



We note that sometimes partial fractions can be avoided when integrating a rational function. For instance, although the integral 
could be evaluated by the method of case III, it's much easier to observe that if u = x(x2 + 3) = x3 + 3x, then du = (3x2 + 3) dx and so 
|
204 videos|290 docs|139 tests
|
FAQs on Integrals of Some Functions - Mathematics (Maths) Class 12 - JEE
| 1. What are some standard integrals that are commonly used in calculus? |  |
| 2. How can we integrate irrational functions in calculus? |  |
| 3. How do we integrate expressions of the form ∫(ax + b)(cx + d)dx in calculus? |  |
| 4. What is the process of integration by substitution and when is it used in calculus? |  |
| 5. Can you explain the concept of integration by parts and provide an example in calculus? |  |

|
Explore Courses for JEE exam
|

|

















