Product of Vectors | Mathematics (Maths) for JEE Main & Advanced PDF Download
Vector Triple Product
Vector Triple Product is a concept in vector algebra that involves taking the cross product of three vectors. To find its value, you calculate the cross product of one vector with the cross product of the other two vectors. The result is a new vector.
Consider next the cross product of
This is a vector perpendicular to both a is normal to the plane of
so
must lie in this plane. It is therefore expressible in terms of
in the form
To find the actual expression for
consider unit vectors j^ and k^ the first parallel to
and the second perpendicular to it in the plane
In terms of j^ and k^ and the other unit vector î of the right-handed system, the remaining vector be written
Then
and the triple product
This is the required expression for in terms of
Similarly the triple product ...(2)
It will be noticed that the expansions (1) and (2) are both written down by the same rule. Each scalar product involves the factor outside the bracket; and the first is the scalar product of the extremes.
In a vector triple product the position of the brackets cannot be changed without altering the value of the product. For is a vector expressible in terms of
is one expressible in terms of
The products in general therefore represent different vectors. If a vector r is resolved into two others in the plane of
one parallel to and the other perpendicular to it, the former is
and therefore the latter
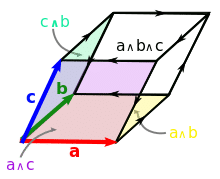
Geometrical Interpretation of
Consider the expression which itself is a vector, since it is a cross product of two vectors
Now
is a vector perpendicular to the plane containing
vector perpendicular to the plane
therefore
is a vector lies in the plane of
and perpendicular to a . Hence we can express
in terms of
i.e.
where x & y are scalars.
Vector Triple Product Formula
The vector triple product formula can be written as:
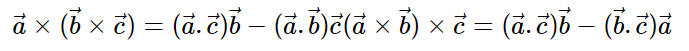
Example: Find a vector and is orthogonal to the vector
It is given that the projection of
Solution: A vector coplanar with is parallel to the triple product,
Example: ABCD is a tetrahedron with A(–5, 22, 5); B(1, 2, 3); C(4, 3, 2); D(–1, 2, –3). Find What can you say about the values of
Calculate the volume of the tetrahedron ABCD and the vector area of the triangle AEF where the quadrilateral ABDE and quadrilateral ABCF are parallelograms.
Solution:
Example: Let a x b=c, b x c=a, and a, b, c be the moduli of the vectors a, b, c, then find a and b.
Solution: a = b × c and a × b = c
∴ a is perpendicular to b and c, and c is perpendicular to a and b.
a, b, and c are perpendicular to each other
Now, a = b × c = b × (a × b) = (b . b) a − (b . a) b or
a =b2 a − (b.a) b= b2 a, {because a⊥b}
⇒1= b .Therefore, 𝑐 = 𝑎×𝑏 = 𝑎𝑏𝑠𝑖𝑛900ń
Taking the moduli of both sides, c = ab, but b = 1 ⇒ c = a.
Example: Given these simultaneous equations for two vectors x and y.
x + y = a …..(i)
x × y = b …..(ii)
x . a = 1 …..(iii)
Find the values of x and y.
Solution: By multiplying (i) scalarly by a, we get
a . x + a . y = a2
∴ a . y = a2 − 1 ..(iv),
{By (iii)} Again a × (x × y) = a × b or (a . y) x − (a . x) y = a × b
(a2 − 1) x − y = a × b ..(v),
Adding and subtracting (i) and (v),
we get x = 𝑎+(𝑎×𝑏) / [a2] and y = a − x
Applications of Vector Triple Product
The vector triple product isn't just a mathematical curiosity; it finds practical applications in various fields:
- Classical Mechanics: It helps calculate the torque acting on a rigid body and analyse the motion of charged particles in magnetic fields.
- Electromagnetism: It comes in handy when dealing with electromagnetic fields and their interactions with matter.
- Crystallography: It plays a crucial role in understanding the arrangement of atoms in crystals and predicting their properties.
Product of Four Vectors
(a) Scalar Product of Four Vectors: The products already considered are usually sufficient for practical applications. But we occasionally meet with products of four vectors of the following types. Consider the scalar product of This is a number easily expressible in terms of the scalar products of the individual vectors. For, in virtue of the fact that in a scalar triple product the dot and cross may be interchanged, we may write
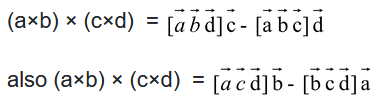
Writing this result in the form of a determinant,
we have
(b) Vector Product of Four Vectors:
Consider next the vector product of This is a vector at right angles to
and therefore coplanar with
Similarly it is coplanar with
It must therefore be parallel to the line of intersection of a plane parallel to
with another parallel to
To express the product in in terms of
regard it as the vector triple product of
and
Similarly, regarding it as the vector product of we may write it
Equating these two expressions we have a relation between the four vectors
...(3)
Example: Show that ,
Sol.
Example: Show that
Sol:
Vector Equations
Vector Equations
Example: Solve the equation
Sol. From the vector product of each member with a, and obtain
Example: Solve the simultaneous equations
Sol. Multiply the first vectorially by
which is of the same form as the equation in the preceding example.
Thus
Substitution of this value in the first equation gives
Example:
Sol. Multiply scalarly by
Example: then prove that
Sol.
...(1)
Solving (2) and simultaneously we get the desired result.
Example: Solve the vector equation in
Sol. Taking dot with a = ...(1)
Taking cross with a = ...(2)
Example: Express a vector as a linear combination of a vector
and another perpendicular to A and coplanar with
and
.
Sol. is a vector perpendicular to
and coplanar with
and
.
Hence let,
...(1)
taking dot with
again taking cross with
|
176 videos|582 docs|160 tests
|
FAQs on Product of Vectors - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the formula for the vector triple product? |  |
| 2. How is the vector triple product used in applications? |  |
| 3. How can vector equations be represented using the vector triple product? |  |
| 4. What are some common examples of vector triple product calculations? |  |
| 5. Why is understanding the vector triple product important in vector calculus? |  |






















