Independent Events and Their Important Properties | Mathematics (Maths) Class 12 - JEE PDF Download
Independent Events
Two events A & B are said to be independent if occurrence or non occurrence of one does not effect the probability of the occurrence or non occurence of other.
(a) If the occurrence of one event affects the probability of the occurrence of the other event then the events are said to be dependent or Contingent. For two independent events A and B

. P(B). Often this is taken as the definition of independent events.
(b) Three events A, B & C are independent if & only if all the following conditions hold ;
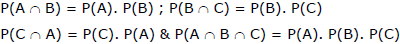
i.e., they must be pairwise as well as mutually independent.
Similarly for n events A1, A2, A3, ........... An to be independent, the number of these conditions is equal to nC2 + nC3 + ............. + nCn = 2n - n - 1.
Note : Independent events are not in general mutually exclusive & vice versa.
Mutually exclusiveness can be used when the events are taken from the same experiment & independence can be used when the events are taken from different experiments.
Ex.1 The probability that an anti aircraft gun can hit an enemy plane at the first, second and third shot are 0.6, 0.7 and 0.1 respectively. The probability that the gun hits the plane is
Sol. Let the events of hitting the enemy plane at the first, second and third shot are respectively A, B and C. Then as given P(A) = 0.6, P(B) = 0.7, P(C) = 0.1
Since events A, B, C are independent, so
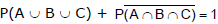
⇒
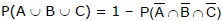
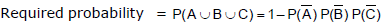
= 1 - (1 - 0.6) (1 - 0.7) (1 - 0.1)) = 1 - (0.4)(0.3)(0.9) = 1 - 0.108 = 0.892
Ex.2 If two events A and B are such that

, P(B) = 0.4 and

then

equals
Sol.
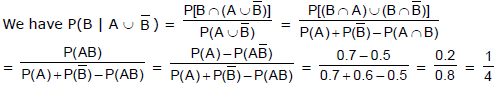
Probability of Three Events
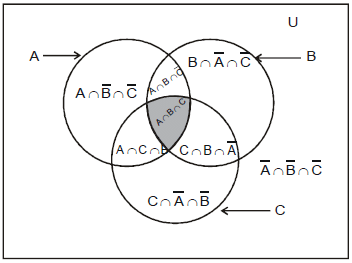
For any three events A, B and C we have
(a) P(A or B or C) = P(A) + P(B) + P(C) – P(A∩B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
(b) P (at least two of A, B, C occur) = P(B ∩ C) + P (C ∩ A) + P(A ∩ B) – 2P (A ∩ B ∩ C)
(c) P (exactly two of A, B, C occur) = P(B ∩ C) + P (C ∩ A) + P(A ∩ B) – 3P (A ∩ B ∩ C)
(d) P (exactly one of A, B, C occurs) = P(A) + P(B) + P(C) – 2P (B ∩ C) – 2P (C ∩ A) – 2P (A ∩ B) + 3P (A ∩ B ∩ C)
|
204 videos|290 docs|139 tests
|
FAQs on Independent Events and Their Important Properties - Mathematics (Maths) Class 12 - JEE
| 1. What are independent events in probability theory? |  |
| 2. What are some important properties of independent events? |  |
| 3. How can the multiplication rule be used to calculate the probability of independent events? |  |
| 4. Can events that are mutually exclusive also be independent? |  |
| 5. How can the concept of independent events be applied in real-life scenarios? |  |

|
Explore Courses for JEE exam
|

|


















