Friction: Its Types and Problems | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| What is Friction? |

|
| Types of Friction |

|
| Angle of Friction |

|
| Angle of Repose (θ) |

|
| Rolling Friction |

|
| Methods of Reducing Friction |

|
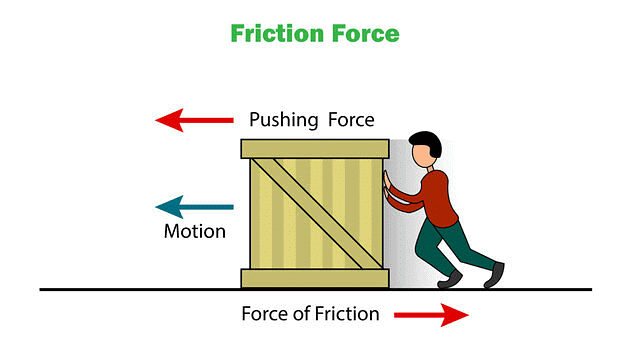
Friction is an invisible force that shows up whenever two surfaces touch and try to move against each other. It resists motion—whether something is sliding, rolling, or just being pushed. For example, when you push a heavy box across the floor, you feel a force pushing back against your hands. That opposing force is friction.
Interestingly, the first person to study and describe friction was Leonardo da Vinci. In this chapter, we will learn what friction is, explore its different types, and understand the key terms related to it.
What is Friction?
Friction is a contact force that always opposes motion. It acts whenever two surfaces touch each other.
- If the object is at rest, friction resists the start of motion.
- If the object is moving, friction works against its motion.
In simple words, friction is the force that tries to stop things from sliding, rolling, or moving on a surface.
Contact Force and Resistance to Movement
- Friction is a contact force because it arises only when two surfaces touch each other.
- Surfaces are never perfectly smooth; they have tiny bumps and irregularities.
- When two surfaces come into contact, these bumps interlock and resist motion.
- This resistance is what we call friction.
Friction is a non-conservative force. When an object moves against friction, some of its energy is always lost as heat.
Types of Friction
Before we proceed further into a detailed account of frictional phenomena, it is advisable to become familiar with different types of frictional forces.
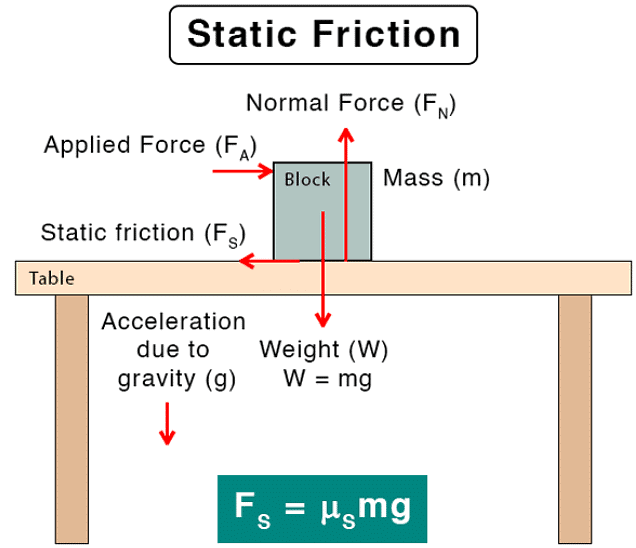
Static Friction
- Static friction occurs when an object is at rest relative to a surface.
- This friction prevents the object from moving when a force is applied until a maximum static friction value is reached.
- Once the applied force surpasses this threshold, the object starts moving, and static friction no longer applies.
- It can have a value maximum up to the limiting friction (fsm).
fs ≤ fsm - The limiting friction is experimentally observed proportional to the normal reaction between surfaces in contact. f= μsN
Here μs is the constant of proportionality. It is known as the coefficient of static friction
for the two surfaces involved.
Examples:
- Preventing a person from slipping while walking or running.
- Keeping a heavy object stationary while pushing or pulling.
 Static Friction
Static Friction
Kinetic Friction
- Kinetic friction comes into play when an object moves relative to a surface after overcoming static friction.
- Kinetic friction is experimentally found proportional to the normal reaction between surfaces in contact. fk = μkN
- Two types of kinetic friction exist:
a) sliding friction for objects sliding over a surface
b) rolling friction for objects rolling on a surface.
Examples:
- Causing a car to skid.
- Bringing a skier to a stop.
 Kinetic Friction
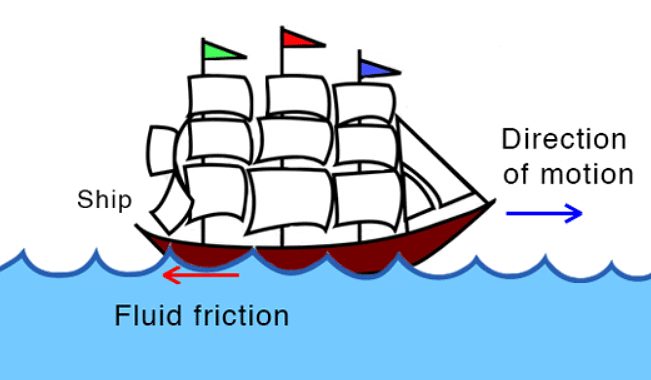
Kinetic FrictionFluid Friction:
- Fluid friction arises when an object moves through a fluid or between layers of moving fluid.
- Fluids can be gases (e.g., air) or liquids (e.g., water), and the friction in some fluids, like oil and water, depends on viscosity.
Examples:
- Creating resistance for a swimmer moving through a pool.
- Impeding the motion of a ship sailing in the ocean.
 Fluid Friction
Fluid Friction
Static and Kinetic Friction in a Box on a Horizontal Surface
To understand the nature of friction let us consider a box of weight W placed on a horizontal rough surface.
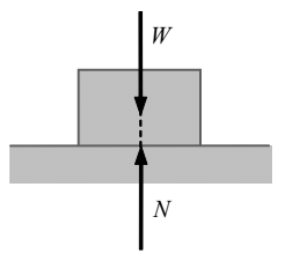
- The forces acting on the box are its weight and reaction from the horizontal surface. They are shown in the figure.
- The weight does not have any horizontal component, so the reaction of the horizontal surface on the box is normal to the surface. It is represented by N in the figure.
- The box is in equilibrium therefore both W and N are equal in magnitude, opposite in direction, and collinear. Now suppose the box is being pulled by a gradually increasing horizontal force F to slide the box.
- Initially, when the force F is small enough, the box does not slide. This can only be explained if we assume a frictional force, which is equal in magnitude and opposite in direction to the applied force F acts on the box.
- The force F produces in the box a tendency of sliding and the friction force is opposing this tendency of sliding. The frictional force developed before sliding initiates is defined as static friction. It opposes the tendency of sliding.
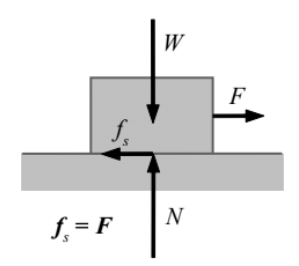 Static Friction
Static Friction
- As we increase F, the box remains stationary until a value of F is reached Kinetic friction when the box starts sliding.
- Before the box starts sliding, the static friction increases with F and counterbalances F until the static friction reaches its maximum value known as limiting friction or maximum static friction fsm.
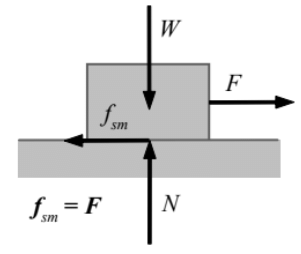 Limiting Friction: The maximum Static Friction
Limiting Friction: The maximum Static Friction
- When the box starts sliding, to maintain it sliding still a force F is needed to overcome frictional force. This frictional force is known as kinetic friction (fk ). It always opposes sliding.
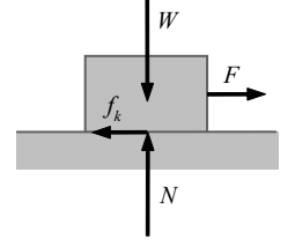 Kinetic Friction
Kinetic Friction
Coefficients of Friction:
- In fk = μkN, μk is the constant of proportionality. It is known as the coefficient of kinetic friction for the two surfaces involved. The frictional forces between any pair of surfaces are determined by the respective coefficients of friction.
- The coefficients of friction are dimensionless constants and have no units. The coefficient of static friction (μs) is generally larger than the coefficient of kinetic friction (μk) but never becomes smaller; at the most, both of them may be equal.
Therefore, the magnitude of kinetic friction is usually smaller than the limiting static friction (fsm), and sometimes kinetic friction becomes equal to the limiting static friction but it can never exceed the limiting friction.
Note:
The limiting static friction and the kinetic friction between any pair of solid surfaces follow these two empirical laws:
(i) Frictional forces are independent of measured area of contact.
(ii) Both the limiting static friction and kinetic friction are proportional to the normal force pressing the surfaces in contact.
Angle of Friction
- When a body is about to slide on a surface, the frictional force and the normal reaction (N) combine to form a resultant contact force.
- The angle between this resultant force and the normal reaction is called the Angle of Friction (λ).
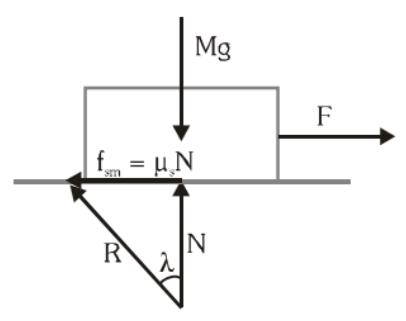 Angle of Friction (λ)
Angle of Friction (λ)
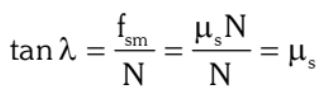
- For a perfectly smooth surface (no friction), λ = 0.
Angle of Repose (θ)
- A body is placed on an inclined plane and the angle of inclination is gradually increased.
- At some angle of inclination θ the body starts sliding down the plane due to gravity.
- This angle of inclination is called the angle of repose (θ).
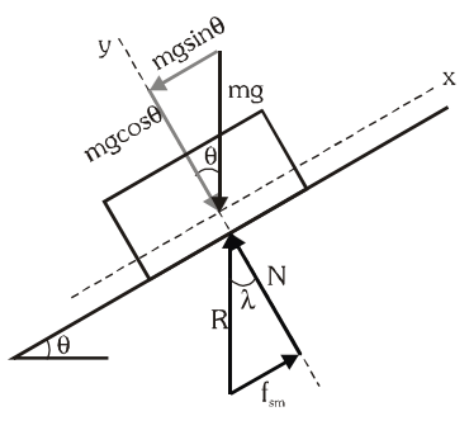 Angle of Repose(θ)
Angle of Repose(θ)
Relation between Angle of Friction and Angle of Repose
- The angle of repose is always equal to the angle of friction.
- In simple terms:
θ = λ
Rolling Friction
When a body rolls without slipping on a surface (like a wheel on a road), a small opposing force comes into play. This is called rolling friction (fr).
Examples
- The wheels of a car rolling on the road
- A cylinder rolling down an inclined plane
- A ball rolling on the ground
Some Key Points are -
Magnitude of rolling friction is much smaller than sliding friction.
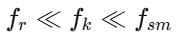
(rolling friction < kinetic friction < limiting static friction)
- Because rolling friction is so small, wheels, ball bearings, and rollers are used in machines to make movement easier.
- Formula for rolling friction:
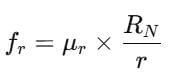
- RN = normal reaction (weight acting on the body)
- r = radius of the rolling body
- μr = coefficient of rolling friction
Unit of μr = metre (unlike coefficients of sliding/static friction, which are dimensionless).
Why is rolling friction smaller?
When an object rolls, there is no continuous interlocking of surface irregularities as in sliding. Instead, a small deformation at the point of contact resists motion, leading to a much smaller opposing force.
Methods of Reducing Friction
Friction is useful in many cases, but sometimes it wastes energy and slows down motion. Here are some common methods to reduce friction:
(a) Polishing
When two surfaces touch, tiny bumps and irregularities interlock and create resistance. By polishing the surfaces, these bumps are smoothed out, so the interlocking reduces. This makes the surfaces glide more easily and lowers friction.
Example: polishing machine parts, tools.
(b) Lubrication
A lubricant (like oil, grease, or graphite powder) is placed between two surfaces. The lubricant forms a thin film that covers the rough spots and prevents direct contact.
Light machines (like sewing machines, watches) use thin oil.
Heavy machines and fast-moving parts use thick oil or grease.
This reduces friction and also prevents wear and tear.
(c) Streamlining
When objects move very fast through air or water, they face air resistance (drag) or fluid resistance. To reduce this, objects are given special streamlined shapes so that air or water can flow smoothly around them.
Examples: airplanes, rockets, cars, trains, even fish and birds have streamlined bodies.
(d) Use of Ball Bearings
Rolling friction is much smaller than sliding friction. To take advantage of this, ball bearings are used.
Small steel balls are placed between moving parts of machines.
Instead of sliding, the balls roll, which reduces friction greatly.
Examples: bicycles, fans, motors, wheels of cars.
(e) Preventing Dust and Moisture
Dust, sand, and moisture on surfaces increase friction because they make the surfaces rougher and cause chemical reactions (like rust).
- By keeping machines clean and dry, friction is reduced.
- Anti-rust coatings, paints, and protective layers are also used to prevent damage.
Example 1: A block of mass 1 kg is at rest on a rough horizontal surface, where coefficients of static and kinetic friction are 0.2 and 0.15.
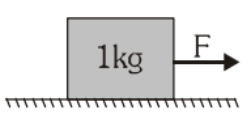 Find the frictional forces if a horizontal force
Find the frictional forces if a horizontal force
(a) F = 1N (b) F = 1.96 N (c) F = 2.5 N is applied on a block
Solution: Maximum force of friction is the limiting friction fsm = 0.2 × 1 × 9.8 N = 1.96 N
(a) For F = 1 N, F < fsm
So, the body is at rest means static friction is present, and hence fs = F = 1 N
(b) For F = 1.96 N, F = fsm = 1.96 N. The block is about to slide, therefore f = 1.96 N
(c) For F = 2.5 N, So F > fsm
Now the body is sliding and kinetic friction acts.
Therefore f = fk = μkN = μk mg = 0.15 × 1 × 9.8 = 1.47 N
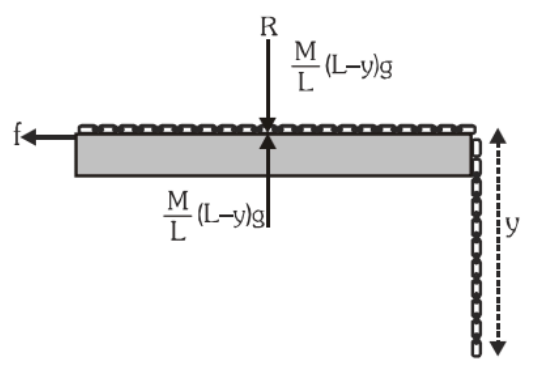
Example 2. The length of a uniform chain is L and the coefficient of static friction is μ between the chain and the tabletop. Calculate the maximum length of the chain that can hang from the table without sliding.
 Solution:
Solution:
We have a chain of total length L. Part of it lies on the table (length = L−y) and part of it hangs over the edge of the table (length = y). The chain is on the verge of sliding.
The friction force between the chain and the table prevents the chain from slipping. The friction force is proportional to the normal force, which equals the weight of the chain lying on the table.
Let:
- L be the total length of the chain
- y be the maximum length hanging outside the table
- μ be the coefficient of static friction
- w be the weight per unit length of the chain
Weight of chain on table = w(L−y)
Weight of chain hanging = wy
Frictional force Ff = μ × Normal force = μw (L−y)
The chain will be on the verge of sliding when frictional force equals weight of hanging part:
μw(L−y) = wy
Simplify and solve for y:
μ(L−y) = y
⇒ μL−μy = y
⇒ μL = y + μy = y(1+μ)
⇒ 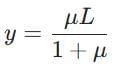
This y is the maximum length of chain that can hang without sliding.
Example 3. A 2 kg body rests on a 5 kg body, which lies on a horizontal surface. The coefficient of friction between the 2 kg body and the 5 kg body is 0.2 and that between the 5 kg body and the horizontal surface is 0.1. Forces of 10 N and 15 N are applied in the same direction on the 2 kg body and the 5 kg body, respectively. Calculate the accelerations of the bodies.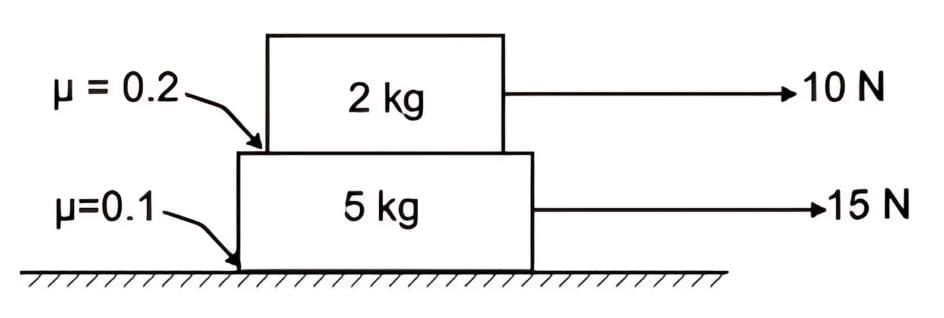
Solution: Given:
- Mass of top block, m₁ = 2 kg
- Mass of bottom block, m₂ = 5 kg
- Coefficient of friction between blocks, μ₁₂ = 0.2 (between blocks)
- Coefficient of friction between bottom block and ground, μg = 0.1 (between lower block and ground)
- Force on top block = 10 N
- Force on bottom block = 15 N
- g = 10 m/s²
Check if both blocks move together
- Normal reaction between the two blocks:
N = m₁ × g = 2 × 10 = 20 N - Maximum static friction:
fₛ(max) = μ₁₂ × N = 0.2 × 20 = 4 N - Friction force on bottom block due to ground:
fground = μg × (m₁ + m₂) × g = 0.1 × 7 × 10 = 7 N - Net external force on system = 10 + 15 – 7 = 18 N
- Common acceleration if both move together:
a =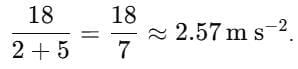
- Friction required to keep the top block moving with this acceleration:
frequired = 10 – (m₁ × a) =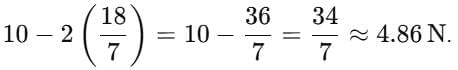
Since frequired (4.86 N) > fₛ(max) (4 N), slipping occurs.
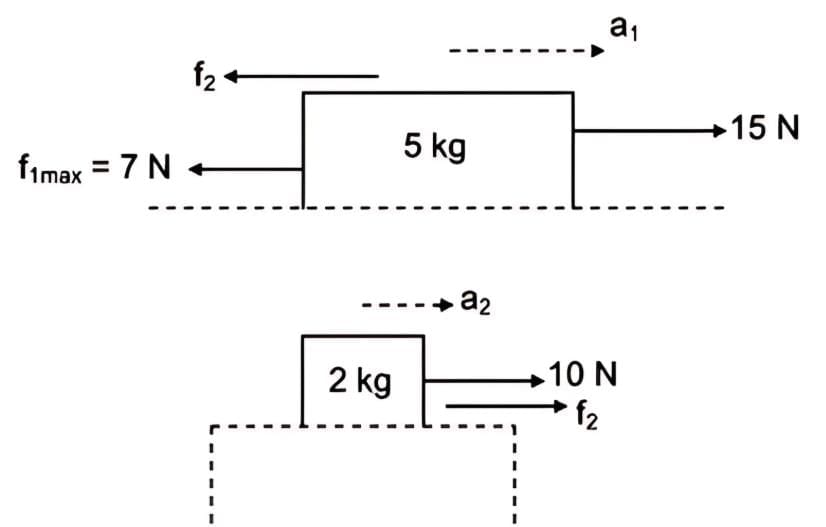
Motion with slipping (kinetic friction acts)
- Kinetic friction between blocks:
fk = μ₁₂ × N = 0.2 × 20 = 4 N - This friction acts left on the 2 kg block and right on the 5 kg block.
- Ground friction on bottom block remains 7 N (to the left).
Calculate accelerations
For top block (m₁ = 2 kg):
- Net force = 10 – 4 = 6 N
- Acceleration, a₁ =
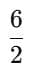 = 3.0 m/s² (to the right)
= 3.0 m/s² (to the right)
For bottom block (m₂ = 5 kg):
- Net force = 15 + 4 – 7 = 12 N
- Acceleration, a₂ =
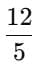 = 2.4 m/s² (to the right)
= 2.4 m/s² (to the right)
|
96 videos|367 docs|98 tests
|
FAQs on Friction: Its Types and Problems - Physics Class 11 - NEET
| 1. What is friction and why is it important in everyday life? |  |
| 2. What are the different types of friction? |  |
| 3. How is the angle of friction defined and what does it signify? |  |
| 4. What is the angle of repose and how is it different from the angle of friction? |  |
| 5. How can problems involving friction be solved in physics? |  |
















