Series AC Circuit | Physics for JEE Main & Advanced PDF Download
3. SERIES AC CIRCUIT
3.1 When only Resistance is in an AC circuit
Consider a simple ac circuit consisting of a resistor of resistance R and an ac generator, as shown in the figure. According to Kirchhoff's loop law at any instant, the algebraic sum of the potential difference around a closed loop in a circuit must be zero.
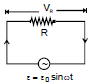
ε - VR = 0
ε - iRR = 0
ε0 sinωt - iRR = 0
iR = sinωt = i0 sin ωt ..(i)
where i0 is the maximum current. i0 =
From above equations, we see that the instantaneous voltage drop across the resistor
VR = i0R sinωt ...(ii)
We see in equation (i) & (ii), iR and VR both vary as sin wt and reach their maximum values at the same time as shown in figure (a), they are said to be in phase. A phasor diagram is used to represent phase relationships. The lengths of the arrows correspond to V0 and i0. The projections of the arrows onto the vertical axis give VR and iR. In case of the single-loop resistive circuit, the current and voltage phasors lie along the same line, as shown in figure (b), because iR and VR are in phase.
3.2 When only Inductor is in An AC circuit
Now consider an ac circuit consisting only of an Inductor of inductance L connected to the terminals of an ac generator, as shown in the figure. The induced emf across the inductor is given by Ldi/dt. On applying Kirchhoff's loop rule to the circuit
ε- VL = 0 ⇒ ε - L
When we rearrange this equation and substitute
ε = ε0 sin ωt, we get 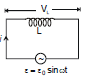
= ε0 sin ωt ...(iii)
Integration of this expression gives the current as a function of time
iL = = -
For average value of current over one time period to be zero, C = 0
Therefore, iL = -
When we use the trigonometric identity
coswt = - sin(wt - p/2), we can express equation as
iL = ...(iv)
From equation (iv), we see that the current reaches its maximum values when cos wt = 1.
i0 = =
...(v)
where the quantity XL, called the inductive reactance, is
XL = ωL
The expression for the rms current is similar to equation (v), with ε0 replaced by εrms.
Inductive reactance, like resistance, has unit of ohm.
We can think of equation (v) as Ohm's law for an inductive circuit.
On comparing result of equation (iv) with equation (iii), we can see that the current and voltage are out of phase with each other by π/2 rad, or 90º. A plot of voltage and current versus time is given in figure (a). The voltage reaches its maximum value one quarter of an oscillation period before the current reaches its maximum value. The corresponding phasor diagram for this circuit is shown in figure (b). Thus, we see that for a sinusoidal applied voltage, the current in an inductor always lags behind the voltage across the inductor by 90º.
Ex.4 An inductor of inductance L = 5 H is connected to an
AC source having voltage v = 10 sin (10t + )
Find 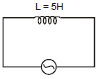
(i) Inductive Reactance (xL)
(ii) Peak & Rms voltage (V0 & Vrms)
(iii) Peak & Rms current (I0 & Irms)
(iv) Instantaneous current (I(t))
Sol. (i) xL = ωL = 10 × 5 = 50
(ii) v0 = 10
vrms =
(iii)
Irms =
(iv) I(t) = 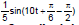
3.3 When only Capacitor is in An AC circuit
Figure shows an ac circuit consisting of a capacitor of capacitance C connected across the terminals of an ac generator. On applying Kirchhoff's loop rule to this circuit, we get
ε - VC = 0
VC = ε = ε0 sin ωt ...(vi)
where VC is the instantaneous voltage drop across the capacitor. From the definition of capacitance, VC = Q/C, and this value for VC substituted into equation gives
Q = C ε0 sin ωt
Since i = dQ/dt, on differentiating above equation gives the instantaneous current in the circuit.
Here again we see that the current is not in phase with the voltage drop across the capacitor, given by equation (vi). Using the trigonometric identity cos ωt = sin(ωt + π/2), we can express this equation in the alternative from
...(vii)
From equation (vii), we see that the current in the circuit reaches its maximum value when cos ωt= 1.
Where XC is called the capacitive reactance.
The SI unit of XC is also ohm. The rms current is given by an expression similar to equation with V0 replaced by Vrms.
Combining equation (vi) & (vii), we can express the instantaneous voltage drop across the capacitor as
VC = V0 sin ωt = i0 XC sin ωt
Comparing the result of equation (v) with equation (vi), we see that the current is π/2 rad = 90º out of phase with the voltage across the capacitor. A plot of current and voltage versus time, shows that the current reaches its maximum value one quarter of a cycle sooner than the voltage reaches its maximum value. The corresponding phasor diagram is shown in the figure (b). Thus we see that for a sinusoidally applied emf, the current always leads the voltage across a capacitor by 90º.
Brain Teaser
What is the reactance of a capacitor connected to a constant DC source ?
Ex.5 A capacitor of capacitive reactance 5? is connected with A.C. source having voltage V = 3 sin (ωt + p/6). Find rms and Peak voltage rms and peak current and instantaneous current
Sol. On comparing with
⇒ v0 = 3
⇒
⇒ I(t) = I0 sin
|
268 videos|740 docs|171 tests
|
FAQs on Series AC Circuit - Physics for JEE Main & Advanced
| 1. What is an AC circuit? |  |
| 2. How does an AC circuit differ from a DC circuit? |  |
| 3. What is the significance of series AC circuits? |  |
| 4. How do we calculate the impedance in a series AC circuit? |  |
| 5. What is the power factor in a series AC circuit? |  |





















