Maxwell's Equations & Displacement Current - Physics Class 12 - NEET PDF

Students are introduced here to Maxwell's equations and the concept of displacement current. These four equations form the foundation of classical electromagnetism and describe how electric and magnetic fields are produced by charges, currents and by each other. The presentation below is kept introductory, precise and aligned to school and competitive-exam requirements.

Maxwell's Equations

James Clerk Maxwell formulated these relations in the 19th century. Together they explain static and time-varying electric and magnetic fields, and predict electromagnetic waves (light). Each equation has an integral form (useful for symmetry arguments and boundary conditions) and a differential form (local form used in field theory).

James Maxwell

1. Gauss's Law for Electricity

Integral form: ∮ E · dA = Q_enclosed / ε₀

Differential form: ∇ · E = ρ / ε₀

• E is the electric field (vector).
• ρ is the volume charge density.
• ε₀ is the permittivity of free space.
• The law states that the net electric flux through a closed surface equals the total enclosed charge divided by ε₀.

2. Gauss's Law for Magnetism

Integral form: ∮ B · dA = 0

Differential form: ∇ · B = 0

• B is the magnetic field (vector).
• This law means magnetic field lines are continuous closed loops and there are no isolated magnetic charges (no magnetic monopoles observed).

3. Faraday's Law of Electromagnetic Induction

Integral form: ∮ E · dl = - d/dt ∫ B · dA

Differential form: ∇ × E = - ∂B / ∂t

• A time-varying magnetic field produces a circulating electric field.
• This is the principle behind transformers, electric generators and induced emf in coils.

4. Ampère's Law with Maxwell's Addition (Ampère-Maxwell Law)

Ampère's law relates the magnetic field around a closed loop to the electric current passing through the loop. Maxwell added a term to this law to account for the displacement current, making it consistent with the continuity equation. The modified equation is:

where J is the current density and 

Displacement Current

Why Maxwell introduced displacement current: Consider the continuity equation ∇ · J + ∂ρ/∂t = 0 which expresses charge conservation. If Ampère's law had only the conduction current term μ₀J, taking divergence of both sides would give a contradiction unless ∂ρ/∂t = 0. To remove this inconsistency Maxwell added the term μ₀ε₀ ∂E/∂t so that the modified law is compatible with charge conservation in regions where charges accumulate (for example, between capacitor plates).

• Definition: The displacement current density is J_D = ∂D / ∂t, where D is the electric displacement field. In vacuum D = ε₀ E and, in a linear dielectric, D = ε E.
• Displacement current: The quantity that contributes to the magnetic field in regions where there is a time-varying electric field but no actual charge carriers moving. Its unit is ampere per square metre (A m^-2).
• Between capacitor plates: When a capacitor charges, conduction current flows in the wires but not across the insulating gap. The changing electric field between the plates produces a displacement current which produces the same magnetic field as the conduction current in the wires, ensuring the continuity of magnetic field lines and consistency of Ampère's law.

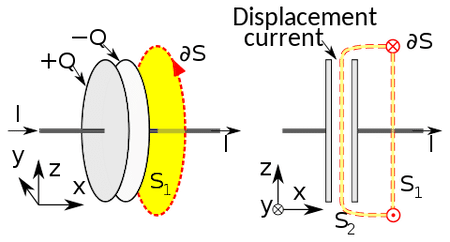Displacement current in a capacitor

Relation between displacement current and total current across a surface:

ID = ∫ J_D · dA = ∫ ∂D/∂t · dA = d/dt ∫ D · dA

• For a capacitor with plate area S and uniform field, ID = J_D S = S (∂D / ∂t).
• Where S is the area of the capacitor plate, I_D is the displacement current, J_D is the displacement current density, D is related to E by D = ε E, and ε is the permittivity of the medium between the plates.
• Thus, displacement current is not the motion of charges across the dielectric; it represents the time rate of change of electric displacement and so completes the symmetry with magnetic effects.

Examples and Applications

• Charging capacitor: In the circuit branch containing a charging capacitor, conduction current exists in the external wires, while between the capacitor plates the changing electric field corresponds to a displacement current. Both give the same magnetic effect in surrounding space.
• Electromagnetic waves: Maxwell's addition made the set of equations symmetric and led to wave solutions in free space; the speed of these waves is c = 1 / √(μ₀ ε₀), identified with the speed of light.
• Practical devices: Faraday's law underlies transformers and generators; the Ampère-Maxwell law is essential in the design of antennas and understanding radiation from time-varying currents.

Summary

Maxwell's equations - Gauss's laws for electricity and magnetism, Faraday's law and the Ampère-Maxwell law - together describe how electric and magnetic fields originate and evolve. The displacement current, J_D = ∂D/∂t, introduced by Maxwell, is essential to preserve charge conservation and to predict electromagnetic waves. Understanding these equations and their integral and differential forms is fundamental to electromagnetism and to many devices encountered in physics and engineering.