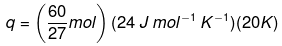Enthalpy, Heat Capacities & Thermochemistry | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| Enthalpy (H) |

|
| Sign Convention of Enthalpy |

|
| Heat Capacity of System |

|
| Degrees of Freedom |

|
| Law of Equipartition of Energy |

|
| Thermochemistry |

|
| Different Types of Enthalpies |

|
| Born Haber Cycle |

|
Enthalpy (H)
The quantity U + PV is known as the enthalpy of the system and is denoted by H. It represents the total energy stored in the system. It is the sum of internal energy and pV-energy of the system. It is a state function and extensive property.
Mathematically
| H = U + PV |
The absolute value of enthalpy can not be determined, however the change in enthalpy can be experimentally determined.
ΔH = ΔU + Δ(PV)
Like U, absolute value of H also cannot be known, ΔH is determined experimentally.
ΔH = H2 – H1
or ΣHp = ΣHR
For exothermic reaction (the reaction in which heat is evolved), ΔH = -ve whereas for endothermic reaction (the reaction in which heat is absorbed), ΔH = +ve.
Derivation of Formula
We may write equation ∆U=q + w as ∆U= qp -P∆V at constant pressure, where qp is heat absorbed by the system and –p∆V represent expansion work done by the system.
Let us represent the initial state by subscript 1 and final state by 2 We can rewrite the above equation as
U2 – U1 = qp – p (V2 – V1)
On rearranging, we get
qp = (U2 + pV2) – (U1 + pV1) -----------(1)
Now we can define another thermodynamic function, the enthalpy H [Greek word enthalpien, to warm or heat content] as :
H = U + pV
so, equation (1) becomes
qp = H2 – H1 = ΔH
ΔH = ΔU + pΔV ...................(2)
Although q is a path dependent function, H is a state function because it depends on U, p and V, all of which are state functions.
Therefore, ∆H is independent of path i.e a State function . Hence, qp is also independent of path.
Relationship between ΔH and ΔU
ΔH = ΔU + Δp Δ V
Let us consider a reaction involving gases. If VA is the total volume of the gaseous reactants, VB is the total volume of the gaseous products, nA is the number of moles of gaseous reactants and nB is the number of moles of gaseous products, all at constant pressure and temperature, then using the ideal gas law, we write,
pVA = nART
and pVB = nBRT
Thus, pVB – pVA = nBRT – nART = (nB – nA)RT
or p (VB – VA) = (nB – nA) RT
or p ∆V = ∆ngRT -----------(3)
Here, ∆ng refers to the number of moles of gaseous products minus the number of moles of gaseous reactants.
Substituting the value of p ∆V from equation (3) in equation (2), we get
| ∆H = ∆U + ∆ngRT |
It is important to note that when heat is absorbed by the system at constant pressure, we are actually measuring changes in the enthalpy.
Remember ΔH = qv, heat absorbed by the system at constant pressure.
Sign Convention of Enthalpy
- ΔH is negative for exothermic reactions which evolve heat during the reaction
- ΔH is positive for endothermic reactions which absorb heat from the surroundings.
At constant volume (ΔV = 0), ΔU = qV, therefore equation becomes ΔH = ΔU = qV
Heat Capacity of System
Heat Capacity (c) of a system is defined as the amount of heat required to raise the temperature of a system by 1°C.
Let a very small quantity of heat dq be given to a system and the temperature of the system rises by dT
Heat capacity = dq/dT
- The SI unit of heat capacity is joule per kelvin (J/K).
- Heat capacity is an extensive property.
Molar Heat Capacity
Molar heat capacity is the amount of heat needed to raise the temperature of 1 mole of a substance by 1 Kelvin.
The SI unit of molar heat capacity is J/mol/K
Specific Heat Capacity
It is the amount of energy that must be added, in the form of heat, to one unit of mass of the substance in order to cause an increase of one unit in its temperature.
q = mc ΔT |
where,
- m = mass of substance
- c is the specific heat, and
- ΔT is the temperature change.
The heat capacity of a system, particularly in a gaseous system, determined at constant volume, is different from that determined at constant pressure.
- At constant volume qV = ΔU=CV ΔT
Molar sp. heat at constant volume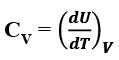
- At constant pressure qp = ΔH=CP ΔT
Molar specific heat at constant pressure
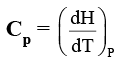
For a mole of an ideal gas,
ΔH = ΔU + Δ(pV) = ΔU + Δ(RT) = ΔU + RΔT
=> ΔH = ΔU+ R
On putting the values of ΔH and ΔU,
we have
CP ΔT = CV ΔT + R ΔT
CP ΔT - CV ΔT = R ΔT
ΔT (CP - CV ) = R ΔT
| CP - CV = R |
(Cp and CV are specific heats at constant pressure and constant volume respectively)
Cp – CV = R (R = Molar gas constant)
The molar heat capacity at constant volume, CV = (3 / 2) R
The molar heat capacity at constant pressure,
Cp = (3 / 2) R + R = (5 / 2)R
Ratio of heat capacity γ = Cp / CV depends on atomicity of gas.
Poisson’s ratio, γ = Cp / CV = (5 / 3) = 1.66
γ = 1.66 for monoatomic gas
γ = 1.40 for diatomic gas
γ = 1.33 for triatomic gas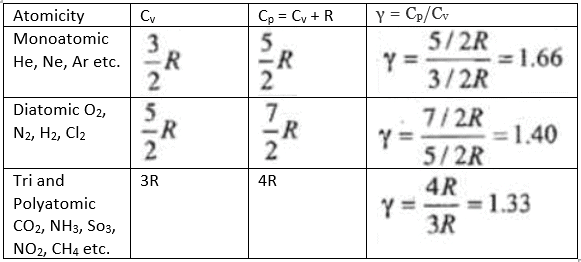
Solved Examples
Example 1. Calculate the energy needed to raise the temperature of 10 g of iron from 25 degree Celsius to 500 degree Celsius if specific heat capacity of iron is 0.45 J g -1˚C -1.
Solution: Here change in temp.=500 - 25=475 ˚C
Total heat = mass × Specific Heat Capacity × change in temp
= m × Cs × ∆T
=10 × 0.45 × 475
=2137.5 Joules
Example 2. Calculate the number of kJ of heat necessary to raise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 J mol–1 K–1.
Solution. From the expression of heat (q),
q = m. c. ΔT
Where,
c = molar heat capacity
m = mass of substance
ΔT = change in temperature
Substituting the values in the expression of q:
q = 1066.7 J
q = 1.07 kJ
Degrees of Freedom
The number of independent variables or coordinates needed to describe the motion of a particle is called the degree of freedom.
- Total number of DOF = 3N (where N = atomicity)
- No. of translational DOF (ft) = 3 (for all gases)
- No. of rotational DOF (fr) = 0 (for monoatomic gas)
No. of rotational DOF (fr) = 2 (for diatomic gas)
No. of rotational DOF (fr) = 2 (for polyatomic linear molecules)
No. of rotational DOF (fr) = 3 (for polyatomic nonlinear molecule) - No. of vibrational dof (fv) = 3N - ft - fr
In a monoatomic species, rotational and vibrational modes of motion are absent. Hence three degrees of freedom corresponds to three translational motion along three different axes.
For a diatomic molecule, total degree of freedom = 3 × 2 = 6
Break up of the Degree of Freedom:
(i) 3 translation degrees of freedom representing translation motion of center of mass in three independent directions.(ii) Two possible axes of rotation, hence two rotational degrees of freedom.
(iii) One vibration degree of freedom.
Vibrational DOF is active only at high temperatures.
Example. Find the total degree of freedom and break up as translational, rotational, or vibrational DOFs in following cases.
(i) O = C = O
(ii)
(iii) He
(iv) NH3
Solution.
(i) CO2: Total dof = 3 x 3 = 9
Translational = 3
Rotational = 2 (∵ linear molecule)
Vibrational = 4(ii) SO2: Total dof = 3 x 3 = 9
Translational = 3
Rotational = 3 (∵ Bent molecule)
Vibrational = 3(iii) He: Total dof = 3 (∵ Monoatomic molecule)
Translational = 3(iv) NH3: Total dof = 3 x 4 = 12
Translational = 3
Rotational = 3 (∵ non linear molecule)
Vibrational = 6
Law of Equipartition of Energy
Energy equal to ½ kT is associated with each translational and rotational degree of freedom per ideal gas molecule.
Energy equal to kT is associated with each vibrational degree of freedom per ideal gas molecule.
Where k = R/NA Boltzmann constant
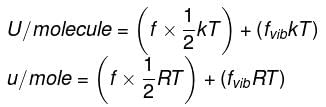
∴ For n moles,
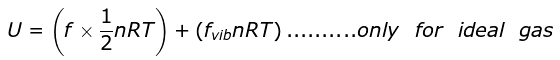
On ignoring vibrational degree of freedom
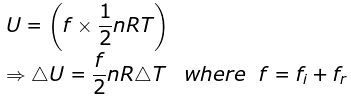
Thermochemistry
Thermochemistry is the branch of physical chemistry which deals with the thermal or heat changes caused by chemical reactions.
Specific heat (s)
Amount of energy required to raise the temp by 1ºC of 1 gm of a substance.Unit → J/kg-K
Heat Capacity (ms)
The amount of heat required to raise the temperature by 1ºC or 1K of a given amount of a substance.Units → J/K
Total heat given to increase the temperature by Δt.
q = msΔt
Molar Heat Capacity (Cm)
The amount of heat required to raise the temp by 1º of 1 mole of a substance.Classification of Molar heat Capacity
(a) Molar heat capacity at constant pressure (Cp,m)(b) Molar heat capacity at constant volume (Cv,m)
Relation between Cp and Cv
| Cp - Cv = R (Mayor's formula) Cp / Cv = γ (Poison's Ratio) |
Rules for Thermochemical Equation
(1) It is necessary to mention physical state of all reactants and products.
(2) A → B, ΔH = HB - HA
If A → B x kJ/mole
ΔH < 0 → (Exothermic reaction)
ΔH = -x kJ/mole
If A x kJ/mole → B
ΔH > 0 → (Endothermic reaction)
ΔH = + x kJ/mole
(3) After reversing a thermochemical eqn then sign of enthalpy also get changed.
Example:
A(g) + B(g) → C(g) + D(g) , ΔH = x kJ
C(g) + D(g) → A(g)+ B(g) , ΔH = - x kJ
(4) When two reactions are added their enthalpies are also get added with their sign.
Example:
A(g) + B(g) → C(g) D(g) ΔH = x1 kJ
C(g) + E(g) → F(g) ΔH = - x2 kJ
A(g) + B(g) + E(g) → D(g) + F(g) , ΔH = x1- x2
(5) If a thermochemical equation is multiplied by a number then DH is multiplied by the same number.
Example:
A(g) + B(g) → C(g) + D(g) ΔH = x1 kJ
2A(g) + 2B(g) → 2C(g) + 2D(g) ΔH = 2x1 kJ
Properties of Matter
Intensive and extensive properties are concepts often used in thermodynamics and other branches of science to describe characteristics of substances or systems.
(i) Intensive Property
The property which does not depend upon the mass of substance is called intensive property.
Example: density, refractive index, specific heat, etc.
(ii) Extensive Property
Mass dependent properties are called extensive properties.
Example:
ΔH, ΔS, ΔG, V, U, Resistance, Number of moles etc.
* Two extensive property can be added
* Ratio of two extensive properties is Intensive.
* Intensive properties can not be added directly.
Example: We can not add the density of two liquids to get the density of the final mixture of the two.
Enthalpy (H)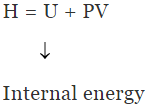 ΔH = ΔU +Δ(PV) = ΔU (P2V2 - P1V1)
ΔH = ΔU +Δ(PV) = ΔU (P2V2 - P1V1)
(i) At constant Pressure, ΔH = ΔU + PΔV
(ii) At Constant Volume, ΔH = ΔU + VΔP
- Enthalpy of ideal gas is function of temperature only.
H = U +PV
= U +nRT - Enthalpy is always defined at constant temperature and it varies with variation in temperature.
For ideal gas, ΔH = ΔU + Δ(PV)
= ΔnCVT +ΔnRT = ΔnT(CV + R)
→ ΔH = Δn CpT Where Δng = no. of moles of gaseous product - no. of moles of gaseous reactant.
Where Δng = no. of moles of gaseous product - no. of moles of gaseous reactant.
Kirchoff's Equation
This gives the relation between enthalpy and temperature.
- Physical state is changed at constant temperature.
According to Hess'Law
ΔH2 + Cp(T2-T1) = ΔH1 + Cp1 (T2- T1)
ΔH2 - ΔH1 = (Cp1 - Cp) (T2- T1)
= ΔCp (T2- T1)
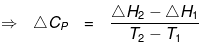
Where
ΔCp = Molar heat capacity of product -- Molar heat capacity of reactant
Example:
N2(g) + 3H2(g) ⇒ 2NH3(g)
ΔCp = 2Cp(NH3) - Cp(N2) - 3Cp(H2)
- If the above formula (Kirchoff's eqn) is to be written for molar heat capacity at constant volume then
- If ΔCp is function of temperature
ΔCp = T2 + T
Then
Different Types of Enthalpies
(i) Heat of formation
Enthalpy change during the formation of 1 mole of a compound form its most stable common occurring form (also called reference states) of elements is called heat of formation.
C(s) + O2(g) ⇒ CO2(g)
ΔH = ΔHf(CO2)
CO(g) + 1/2O2(g) ⇒ CO2(g)
ΔH ≠ ΔHf CO2(g)
(because CO2 has not been formed form its element in their most stable form)
Similarly
Heat of reaction
Element | Most stable form |
H | H2(gas) |
O | O2(gas) |
N | N2(gas) |
F | F2(gas) |
Cl | Cl2(gas) |
Br | Br2(gas) |
I | I2(solid) |
C | C(graphite) |
P | P(white) |
S | S(rhombic) |
All metal except Hg exist in solid form (reference states)
Enthalpy At Standard State :-(ΔHº)
T = 25ºC = 298 K
P = 1 atm
Conc = 1M
ΔHº = Heat of formation at standard state
If A(g) + B(g) ⇒ C(g +D(g) is any reaction, Heat of reaction for any thermochemical equation can be written as
ΔHº = DHfº(product) - DHfº(Reactant)
If we use the above concept for the above given reaction then
ΔHº = DHfº(c) + ΔHfº(D) - ΔHfº(A) + ΔHfº(B)
Assumption:-
The heat of formation of most stable form of an element is taken as zero.
C(graphite) + O2(g) ⇒ CO2(g)
ΔHº = ΔHfº(CO2) - ΔHfºC(s) - ΔHfº(O2)(g)
⇒ ΔHº = ΔHfº(CO2) (As ΔHfºC(s) = 0 and Δ HfºO2(g) = 0)
Another example can be taken as
H2(g) + 1/2O2(g) ⇒ H2O(l)
Example 1. From the following data,
C(s, graphite) O2(g) ⇒ CO2(g) DHº = -393.5 kJ/mole
H2(g) + 1/2O2(g) ⇒ H2O(l) DHº = -286 kJ/mole
2C2H6(g) + 7O2(g) ⇒ 4CO2(g) 6H2O(l) ΔHº = -3120 kJ/mole
Calculate the standard enthalpy of formation of C2H6(g) (in kJ/mole)
Solution. From eqn(1) ΔHfº(CO2) = -393.5 kJ/mole
From eqn(2) ΔHfº(H2O) = -286 kJ/mole
From eqn (3) ΔrHº = 4 ΔHfº(CO2) + 6ΔHfº(H2O) -2 ×ΔHfº(C2H6) - 7×ΔHfºO2(g) - 3120
= 4 ×(-393.5) + 6×(-286) - 2×ΔHfº(C2H6) (As ΔHfº O2(g) = 0)
⇒ -3120 = -1574 -1716 - 2 ×ΔHfº(C2H6)
⇒ -3120 + 3290 = - 2 ×ΔHfº(C2H6)
⇒ 170 = - 2 ×ΔHfº(C2H6)
⇒ ΔHfº = - 85 kJ/mole
(ii) Heat of Combustion
It is the enthalpy change (always -ve) when One mole of the substance undergo complete combustion.
C(s) + O2 ⇒ CO2(g)
ΔHº = ΔHCºC(s) = ΔHfº(CO2) - ΔHfºC(s) - ΔHfº(O2)
ΔHº = = ΔHC ºC(s) = ΔHfº(CO2)
Other example
Note:
Heat of combustion is always exothermic
- N2 + O2 ⇒ 2NO
(It is an endothermic reaction)
- O2 + F2 ⇒ OF2
(Since O has normally tendency to accept electron and opposite is happening above hence reaction is is considered endothermic)
- Heat of reaction for any thermochemical equation can be written as (in form of heat of combustion)
ΔHrº = Heat of combustion of reactant - Heat of combustion of reactant.
ΔHrº = ΔHCº (Reactant) - ΔHCº (Product)
Example 2. The enthalpy change for the reaction
C3H8(g) + H2(g) ⇒ C2H6(g) + CH4(g) at 25ºC is - 55.7 kJ/mole calculate the enthalpy of combustion of C2H6(g). The enthalpy of combustion of H2, and CH4 are - 285.8 and - 890.0 kJ/mole respectively. Enthalpy of combustion of propane is -2220 KJmol-1.
Solution. As we know any thermochemical eqn can be written in terms of heat of combustion as follows
ΔHrº = ΔHcº (Reactant) - ΔHCº (Product)
ΔHrº = ΔHcº (C3H8) +ΔHCº (H2) - {ΔHcº(C2H6)+ ΔHCº(CH4)}
- 55.7 = (-2220 - 285.8) - {-890 +ΔHcº(C2H6)}
⇒ ΔHcº(C2H6) (g) = - 1560.1 kJmol-1
Problems Based on Both HOC and HOF:
Example 3. At 300K, the standard enthalpies of formation of C6H5COOH(s), CO2(g) and H2O(l) are -408, -393 and -286 kJmol-1 respectively. Calculate the enthalpy of combustion of benzoic acid at
(i) constant pressure
(ii) constant volume.
Solution. 7C(s) + 3H2(g)+ O2(g) ⇒ C6H5COOH(s) ΔHº = -408 kJ
⇒ ΔHfº(C6H5COOH) = - 408 kJ
C(s) + O2(g) ⇒ CO2(g) ΔHº = -393 kJ
⇒ ΔHfº(CO2) = -393 kJ
H2(g) + 1/2O2(g) ⇒ H2O(l) ΔHº = -286 kJ
⇒ ΔHfº(H2O) = -286 kJ
C6H5COOH(s) + 15/2O2(g) ⇒ 7CO2(g) + 3H2O(l)
⇒ ΔHCº(C6H5COOH) = 7 ΔHfºCO2 + 3ΔHfº(H2O) - 4ΔHfº(C6H5COOH)
= 7 ×(-393) +3× (-286)- 4(408)
ΔHCº(C6H5COOH) = - 3609 408
= -3201 kJ/mol
⇒ enthalpy of combustion at constant pressure = - 3201 kJ mol-1
Also
ΔH = ΔU + ΔngRT
-3201 = ΔU + (-0.5) × 8.31 × 10-3 × 300
(As Δn = 0.5, R = 8.314 × 10-3 kJ)
⇒ ΔU = - 3201 + 1.2471
ΔU = -3199.7529
⇒ enthalpy of combustion at constant volume = - 3199.7529
Bond Energy
It is defined for gaseous molecules. "The enthalpy change during the breaking of one mole of bond into isolated gaseous atoms is called bond energy of the compound"
Example:
H2(g) ⇒ 2H(g) , ΔHº = ∑H-H
ΔHº = ∑H-H = 2ΔHfºH(g) - ΔHfº(H2)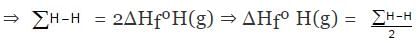
Similarly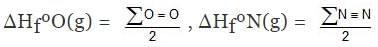
- Let us consider the similar bond breaking In CH4
CH4(g) ⇒ C(g) + 4 H(g)
ΔH = 4 ∑C-H =ΔHfºC(g) 4ΔHfºH(g) - ΔHfº(CH4) - Enthalpy of reaction in terms of bond energy for a thermochemical eqn can be written as
ΔHfº = B.E.(Reactant) - B.E. (products)
Example 4. Using the bond enthalpy data given below, calculate the enthalpy change for the reaction
C2H4 (g) + H2(g) ⇒ C2H6(g)
Data :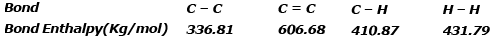
Solution.
ΔrHº = Σreactant - Σproduct
ΔHrº = ΣC = C+4 ΣC-H+ΣH-H -ΣC-C -6ΣC -H
ΔHrº = 606.68 4×410.87 431.79 -336.81 -6×410.87 = 2681.95 -2802.03
ΔHrº = -120.08 kJ/mol
(iii) Heat of hydrogenation
"Enthalpy change during the addition of 1 mole of H2 to an unsaturated compound. is called heat of hydrogentation."
Hydrogenation is an exothermic process. of therefore heat of hytdrogentaiton is always -ve.
Example:
CH2 = CH2 + H2 ⇒ CH3 -CH3
ΔHrº = ΔHº (Hydrogenation of CH2 = CH2)
ΔHrº = ΔHº (Hydrogenation) of cyclohexene
Example 5. Compare the heat of hydrogenation of the following alkene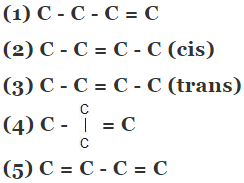
Solution.
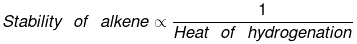
The above concept is true as long as no. of double bonds are equal as heat of hydrogenation is defined for per mole of double bond. It will be certainly larger for higher number of double bonds irrespective of their stability.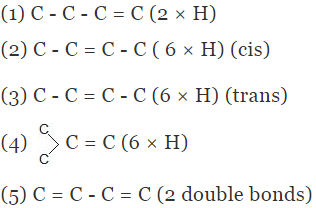
As we know trans > cis (stability)
⇒ Heat of hydrogen (trans) < Heat of hydrogenation (cis)
of therefore decreasing order of heat of hydrogenation of alkene 5 > 1 > 2 > 3 > 4.
Example 6. Find DHf of HCl(g) if bond energies of H2, Cl2 and HCl are 104, 58, 103 kcal/mole respectively.
Solution. H - Cl ⇒ H(g) + Cl(g)
∑H-Cl= ΔHfºH(g) + HfºCl(g) - ΔHfºHCl(g)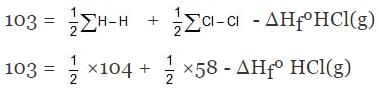
⇒ ΔHfºHCl(g) = - 22 kcal/mol.
(iv) Heat of Atomisation
" When one mole of any substance is converted into gaseous atoms enthalpy change during the process is called heat of atomisation." It is always +ve.
(v) Heat of sublimation
Enthalpy change during the conversion of one mole of solid to 1 mole of gaseous phase directly without undergoing into liquid phase is called enthalpy of sublimation or heat of sublimation,
It is always +ve due to endothermic nature of the process.
Example:
C(s) ⇒ C(g)
ΔHº = ΔHsubºC(s) = ΔHfº C(g) - ΔHfº C(s)
⇒ ΔHsubºC(s) = ΔHfº C(g)
⇒ ΔHsubºC(s) = ΔHfº C(g) = ΔHºatmosationC(g)
Example 7. Using the given data, calculate enthalpy of formation of acetone(g) [All values in kJmol-1] bond enthalpy of C-H = 413.4, C - C = 347.0 (C = O) = 728.0
O = O = 495.0 , H - H = 435.8 DsubH of C = 718.4
Solution.
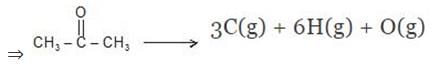
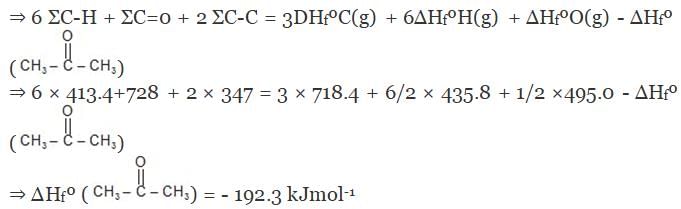
Example 8. The enthalpy of combustion of acetylene is 312 kcal. If enthalpy of formation of CO2 and H2O are -94.38 and -68.38 kcal respectively
Calculate C º C bond enthalpy.
Given that enthalpy of atomisation of 150 kcal and H - H bond enthalpy and C - H bond enthalpy are 103 kcal and 93.64 kcal respectively.
Solution.
HC ≡ CH + 5/2O2 ⇒ 2CO2 + H2O
ΔHCº(CH ≡ CH) = 2ΔHfº(CO2) + ΔHfº(H2O) - ΔHfº(C2H2)
- 312 = 2 × (-94.38) + (-68.38) - ΔHfº(C2H2)
ΔHfº(C2H2) = 54.86
CH ≡ CH ⇒ 2C(g) + 2H(g)
ΣC=C + 2ΣC-H = 2ΔHfºC(g) + 2ΔHfºH(g) - ΔHfº(CH º CH)
ΣC=C + 2 × 93.64 = 2 × 150 2 × (1/2) × 103 -54.86
⇒ ΣC=C = 160.86 kJmol-1
Resonance Energy
"The energy difference between resonance hybrid and most stable canonical structure is called resonance energy".Resonance energy is generally -ve as nature of the process is exothermic.
Example 9. The enthalpy of formation of ethane, ethylene and benzene from the gaseous atoms are -2839.2, -2275.2 and -5506 kJmol-1 respectively. Calculate the resonance energy of benzene. The bond enthalpy of C - H bond is given as equal to 410.87 kJ/mol.
Solution. 2C(g) + 6H(g) ⇒ C2H6 ΔHº = -2839.2
C2H6 ⇒ 2C(g) + 6H(g) ΔHº = 2839.2
∑C - C + 6∑C - H = 2839.2 ΔHº = 2839.2
∑C - C + 6 × 410.87 = 2839.2
∑C - C = 373.98 ... (1)
2C(g) + 4H(g) ⇒ C2H4(g) ΔHº = -2275.2
C2H4 ⇒ 2C(g) + 4H(g) ΔHº = 2275.2
∑C = C + 4∑C - H = 2275.2
∑(C = C) = 631.72 ...(2)
6C(g) + 6H(g) ⇒ C6H6 ΔHº = -5506
⇒ C6H6 ⇒ 6C(g) + 6H(g) ΔHº = 5506
⇒ 3∑C = C + 3∑C - C + 6∑C - H+ x = 5506
Putting all the values from eqn , 1, & (2) we get x = 23.68
⇒ Resonance energy of benzene = - 23.68 kJ/mole
Bomb Calorimeter
Heat evolved = msΔt CΔt
↓
Heat capacity of container
Heat of combustion
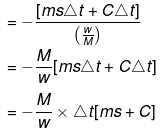
= -
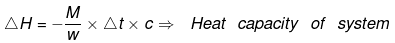
Example 10. When 1.0 gm of fructose C6H12O6 (s) is burnt in oxygen in a bomb calorimeter, the temperature of the calorimeter water increases by 1.56ºC. If the heat capacity of the calorimeter and its contents is 10.0 kJ/ºC. Calculate the enthalpy of combustion of fructose at 298 K.
Solution.
Heat capacity of the system
↑
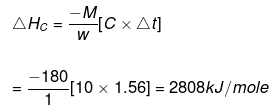
(vi) Heat of solution
Enthalpy change during the dissolution of 1 mole of salt in excess of solvent.
KCl(s) aq ⇒ KCl (aq)
ΔHº = Heat of soln of KCl (s)
Note :-
(1) Heat of solution is always exothermic for the anhydrous form of salts which can form their hydrates.
Example:
CuSO4, Na2SO4, FeSO4, ZnSO4, CaCl2, LiCl etc.
CuSO4(s) aq ⇒ CuSO4(aq) ΔH < 0
(2) Heat of solution is endothermic for the hdyrated form of the salt.
CuSO4 . 5H2O aq ⇒ CuSO4(aq)ΔH > 0
(3) Heat of soln is endothermic for the salts which do not form their hydrates.
Example: NaCl, NaNO3, KCl etc.
Integral Heat of solution
Enthalpy change when 1 mole of salt is dissolved in given amount of solvent.
Example:
KCl(s) + 20 H2O ⇒ KCl (20H2O) -------------(1) DH2 = x
KCl(s) + 100 H2O ⇒ KCl (100H2O) -------------(2) DH2 = y
(vii) Heat of dilution
Reversing the eqn (1) and adding in (2)KCl(20H2O) + 80H2O ⇒ KCl(100H2O)
ΔH = y - x
enthalpy change when the conc. of salt changes from one to another on the basis of dilution
⇒ ΔH = y - x = Heat of dilution
(viii) Heat of hydration
Enthalpy change during the formation of hydrated form of salt from its anhydrous form. It is always exothermic.
CuSO4(s) + 5H2O ⇒ CuSO4.5H2O
ΔH = Heat of hydration of CuSO4(s)
Example 11. Heat of soln of CuSO4(s) and CuSO4.5H2O is 15.9 and 19.3 kJ/mol respectively. Find the heat of hydration of CuSO4(s)
Solution. CuSO4(s) + aq ⇒ CuSO4(aq) ......(1)
ΔH = -15.9
CuSO4.5H2O + aq ⇒ CuSO4(aq) ......(2)
ΔH = 19.3
Reversing eqn (1) and adding (2)
CuSO4(s) + aq ⇒ CuSO4(aq)
ΔH = 15.9
CuSO4.5H2O + aq ⇒ CuSO4(aq)
ΔH = 19.3
CuSO4.5H2O ⇒ CuSO4(s)
ΔH = 35.2
⇒ CuSO4(s) ⇒ CuSO4.5H2O
ΔH = -35.2
⇒ Heat of hydration of CuSO4(s) = -35.2 kJ/mol
(ix) Heat of neutralisation
Enthalpy change during neutralisation of 1 gm equivelant of Acid with 1 gm equivelant of base in dilute soln is called heat of neutralisation.
HCl(aq) + NaoH(aq) ⇒ NaCl + H2O
H + Cl- + Na + OH- ⇒ Na + Cl- + H2O
H (aq) + OH-(aq) ⇒ H2O(aq)
ΔHº = -13.7 Kcal
H2SO4(aq) + 2NaOH(aq) ⇒ Na2SO4 + 2H2O
2H + SO42- + 2Na + 2OH- ⇒ 2Na + SO42- + 2H2O
2H + 2OH- ⇒ 2H2O
⇒ ΔH = -13.7 × 2
Note:-
In case of weak Acid or weak bases the observed value is little lower because of a part of it is used in dissociating weak Acid or weak base which is not at all completely ionised at dilute solution unditions.
These are however, completely ionised at infinite dilution.
Example:
CH3COOH + NaOH ⇒ CH3COONa + H2O
ΔH = -13.7 + x
As we know, H + OH- ⇒ H2O , ΔH = -13.7 kcal ----(1)
CH3COOH ⇒ CH3COO- + H , ΔHº = x ----(2)
Add eqn (1) (2)
CH3COOH + OH- ⇒ CH3COO- + H2O ΔHº = y
Example 12. 100 ml 0.5M H2SO4(strong Acid) is neutralised by 200 ml 0.2 M NH4OH. In a constant pressure calorimeter which results in temperature rise of 1.4ºC. If heat capacity of calorimeter constant is 1.5 kJ/ºC.
Which statement is/are correct.
Given: HCl + NaOH ⇒ NaCl + H2O 57 kJ
CH3COOH + NH4OH ⇒ CH3COONH4 + H2O 48.1 kJ
(A) Ethalpy of neutralisation of HCl v/s NH4OH is -52.5 kJ/mol
(B) Ethalpy of dissociation (ionisation) of NH4OH is 4.5 kJ/mol
(C) Ethalpy of dissociation of CH3COOH is 4.6 kJ/mol
(D) ΔH for 2H2O(l) ⇒ 2H+ (aq) + 2OH-(aq) is 114 kJ
Solution.
(A) Total heat evolved due to the neutralization = C × Δt = 1.5 × 1.4 = 2.1
M. eq of H2SO4 = 100 ×0.5 = 50
M.eq of NH4OH = 20 × 0.2 = 40
Since NH4OH is limiting hence energy will evolved according to it.
⇒ 0.04 gm eq produces 2.1 kJ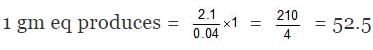
⇒ Heat of neutralisation = -52.5 kJ
(B) -57 + x = - 52.5
⇒ x = - 52.5 + 57 = 4.5
⇒ Enthalpy of dissociation of NH4OH = 4.5 kJ/mol
(C) 57-(x + y) = 48.1
⇒ x + y = 8.9
⇒ 4.5 y = 8.9
⇒ y = 4.4
⇒ enthalpy of dissociation of CH3COOH = 4.4 kJ/mol
(D) As we know
H+ + OH- ⇒ H2O , ΔH = -57
⇒ 2H + 2OH- ⇒ 2H2O , ΔH = -57× 2
⇒ 2H2O ⇒ 2H++ 2OH- , ΔH = 114 kJ
⇒ Option A, B, and D are correct.
Born Haber Cycle
- Ionisation Energy:-The minimum amount of energy required to remove one electron form the outermost shell of an isolated gaseous atom is called ionisation energy of the element.
- Electron affinity:-Amount of energy released when an extra electron is added to an isolated gaseous atom.
- Lattice Energy:- Amount of energy released when 1 mole of gaseous cation and 1 mole gaseous anion combine to each other and form 1 mole of ionic compound is called lattice energy.
Na (g) + Cl-(g) → NaCl(s) + heat (Lattice energy)
Example 13. Calculate the standard enthalpy change for a reaction CO2(g) + H2(g) → CO(g) +H2O (g) given that ΔHf0 for CO2(g), CO(g) and H2O(g) as -393.5, -110.5 and -241.8 KJ/mol respectively.
(A) -31.2 KJ
(B) - 21.2 KJ
(C) -11.2 KJ
(D) 41.2KJ
Ans. (D)
Solution.
ΔHº= SΔHfº(products) - SΔHfº(Reactants)
=
ΔHº = [-241.8 - 110.5] - [-393.5 0]
= - 352.3 393.5 = 41.2 KJ
|
119 videos|346 docs|74 tests
|
FAQs on Enthalpy, Heat Capacities & Thermochemistry - Chemistry Class 11 - NEET
| 1. What is enthalpy and how is it related to thermochemistry? |  |
| 2. What is the significance of the Born-Haber cycle in thermochemistry? |  |
| 3. How are heat capacities related to enthalpy and thermochemistry? |  |
| 4. What are some applications of thermochemistry in real life? |  |
| 5. How can thermochemistry be used to determine the enthalpy of a reaction experimentally? |  |