Sawhorse, Newman, Fischer Projections & their Interconversions. | Organic Chemistry PDF Download
| Table of contents |

|
| Sawhorse Representation |

|
| Newman Projection |

|
| Fischer Projection (2-D representation) |

|
| Flying–Wedge Representation (3-D representation) |

|
| Interconversions |

|
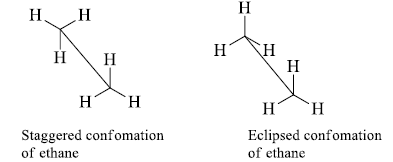
Sawhorse Representation
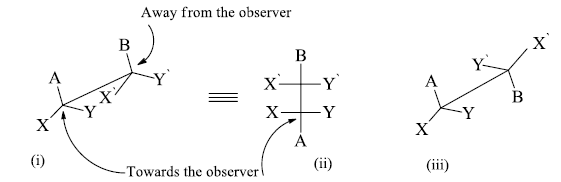
The sawhorse formula indicates the spatial arrangement of all the groups on two adjacent carbon atoms is represented by a diagonal line usually from lower left to upper right.
- The left-handed bottom end represents the atom nearest to the observer and the right-hand top end represents the atom away from the observer.
- Two of the remaining bonds to the two atoms are drawn vertically and the other four at +1200 and-1200 angles.
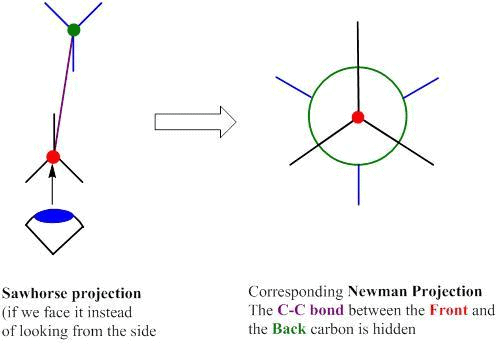
Newman Projection
The Newman projection formula is the planar projection formula of the sawhorse formula.
- Newman projection is similar to the sawhorse projection but represents the spatial arrangements of all the groups on the two carbon atoms.
- Here, a molecule is viewed along the axis of a carbon-carbon bond. The carbon towards the front is represented by a dot (.) and the carbon towards the rear by a circle.

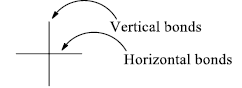
Fischer Projection (2-D representation)
The Fischer projection, devised by Emil Fischer in 1891, is a two-dimensional representation of a three-dimensional organic molecule by projection.
- Horizontal bonds: Points towards the observer
- Vertical bonds: Points away from the observer
Some Important Rules
In order to find out whether the two structures are identical or not, these projections can be manipulated only in specific ways. The following rules must be obeyed.
1. For comparison, a Fischer projection may be rotated 180° in the plane of the paper & molecule remains the same.

2. One interchange in the Fischer projection leads to the enantiomers. Configuration at the
stereocenter changes from (S) to (R) and vice-versa.
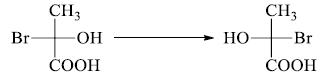
3. Two or any even number of interchanges of the groups at the chiral center, don’t change the configuration.

4. A 900 rotation of the Fischer projection formula about the chiral center inverts the configuration.
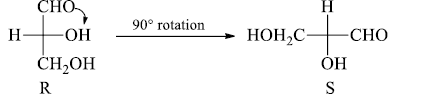
5. It is not permitted to lift projection formulae out of the plane of the paper and flip them over or view them from the opposite side of the paper. These operations, if done, are the same as breaking a bond to change the configuration of the original molecule.
For Example:

6. Fischer projection can be manipulated by rotating a group of any three ligands in a clockwise or anticlockwise direction; the fourth ligand doesn’t change its position (Such a manipulation is equivalent to two interchanges).

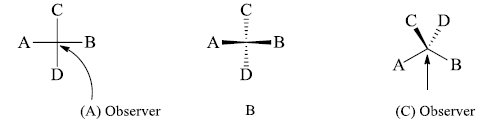
Flying–Wedge Representation (3-D representation)
The Flying-Wedge Projection is the most widely used three-dimensional representation of a molecule on a two-dimensional surface (paper).
This kind of representation is usually done for a molecule containing a chiral center. In this type of representation, three types of lines are used.
- Solid wedge (thick line)- bond above the plane of paper
- Broken wedge (dashed line) – a bond below the plane of the paper
- Continuous lines (solid lines)- bonds in the plane of the paper
Interconversions
Fischer Projection into Flying Wedge and Vice-Versa
- We draw the bonds which are towards the observer by solid wedge and the bonds away from the observer by dashed lines. Then the above-shown molecule becomes.
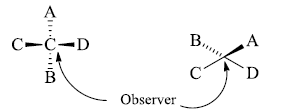
- We want to convert this molecule into a flying wedge projection formula to hold the atoms C and D and start the process of bending so that an inverted V is formed i.e. This inverted v represents the atoms in one plane. Now draw the B below this plane shown below in this formula.
- The atom shown above is represented above the plane in the flying wedge formula.
- We are observing from the bottom of the right side. If we observe from the top of this molecule then we find that
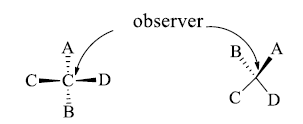
Conversion of Fischer Projection into Sawhorse and Newman Formula
- If we want to convert the eclipsed form of the flying wedge projection into a staggered form then hold C2 atom in hand in its position and rotate the C3 atom by 1800
- The atoms which are towards the observer are away from the observer and the atoms which are away from the observer become towards the observer.
i. Eclipsed conformation (Flying wedge projection).
ii. Eclipsed conformation (Fischer projection).
iii. Staggered conformation (Flying wedge projection).
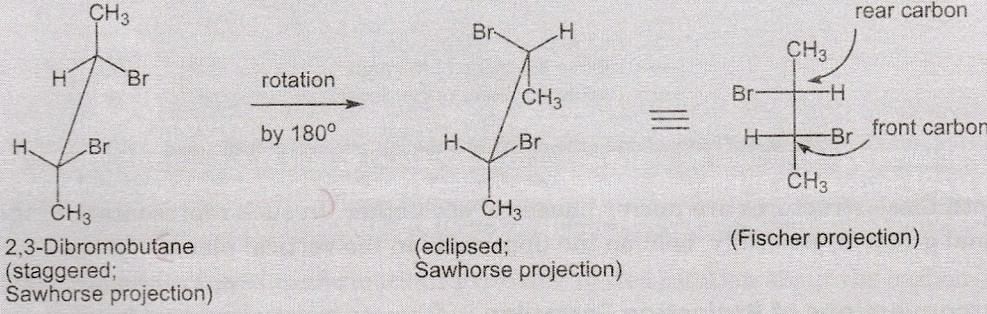 Sawhorse into Fischer Conversion
Sawhorse into Fischer Conversion
Sawhorse Formula into Newman Projection Formula
- We know that the left-handed bottom end is towards the observer and the right-hand top end is away from the observer.
- We can convert this formula into Newman formula representing the molecule i.e. C2 which is towards the observer by a dot (.) and the atom which is away from m the observer i.e. C3 by a circle.
- The Newman projection formula is a planar projection of the sawhorse formula. In this molecule, we view along with the carbon-carbon bond.
- The carbon atom towards the observer is represented by a dot (.) and the carbon atom away from the observer is represented by a circle.
- The above-shown eclipsed form can be converted into a staggered form by a rotation of 1800 of one carbon atom only.
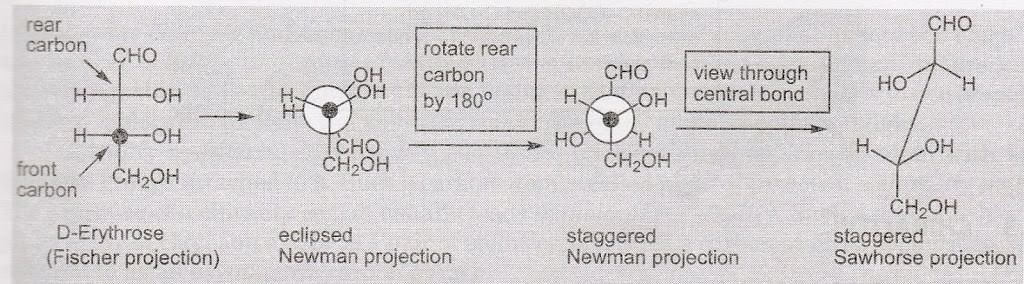 Conversion of Fischer Projection into Sawhorse Projection via Newmann Projection
Conversion of Fischer Projection into Sawhorse Projection via Newmann Projection
|
39 videos|92 docs|46 tests
|
FAQs on Sawhorse, Newman, Fischer Projections & their Interconversions. - Organic Chemistry
| 1. What is the purpose of using Sawhorse, Newman, Fischer Projections in organic chemistry? |  |
| 2. How do you convert a Sawhorse Projection to a Newman Projection? |  |
| 3. What is the advantage of using Fischer Projections over other types of molecular representations? |  |
| 4. How do you interconvert Fischer and Newman Projections? |  |
| 5. Can you provide an example of when using Flying-Wedge Representation is more beneficial than other types of molecular representations? |  |
















