Basic Blocks and Flow Graphs of Code Generation -Code Generation,Computer Science and IT Engineering - Computer Science Engineering (CSE) PDF Download
BASIC BLOCKS AND FLOW GRAPHS
Basic Blocks
- A basic block is a sequence of consecutive statements in which flow of control enters at the beginning and leaves at the end without any halt or possibility of branching except at the end.
- The following sequence of three-address statements forms a basic block
- t1 : = a * a
t2 : = a * b
t3 : = 2 * t2
t4 : = t1 + t3
t5 : = b * b
t6 : = t4 + t5
Basic Block Construction:
Algorithm: Partition into basic blocks
Input: A sequence of three-address statements
Output: A list of basic blocks with each three-address statement in exactly one block Method:
1. We first determine the set of leaders, the first statements of basic blocks. The rules we use are of the following:
a. The first statement is a leader.
b. Any statement that is the target of a conditional or unconditional goto is a leader.
c. Any statement that immediately follows a goto or conditional goto statementis a leader.
2. For each leader, its basic block consists of the leader and all statements up to but not including the next leader or the end of the program.
Consider the following source code for dot product of two vectors:

The three-address code for the above source program is given as :
(1) prod := 0
(2) i := 1
(3) t1 := 4* i
(4) t2 := a[t1] /*compute a[i] */
(5) t3 := 4* i
(6) t4 := b[t3] /*compute b[i] */
(7) t5 := t2*t4
(8) t6 := prod+t5
(9) prod := t6
(10) t7 := i+1
(11) i := t7
(12) if i<=20 goto (3)
Basic block 1: Statement (1) to (2)
Basic block 2: Statement (3) to (12)
Transformations on Basic Blocks:
A number of transformations can be applied to a basic block without expressions computed by the block. Two important classes of transformation are :
- Structure-preserving transformations
- Algebraic transformations
1. Structure preserving transformations:
a) Common subexpression elimination:
a : = b + c - - > a : = b + c
b : = a - d - - > b : = a - d
c : = b + c - - > c : = b + c
d : = a - d - - > d : = b
Since the second and fourth expressions compute the same expression, the basic block can be transformed as above.
b) Dead-code elimination:
Suppose x is dead, that is, never subsequently used, at the point where the statement x : = y + z appears in a basic block. Then this statement may be safely removed without changing the value of the basic block.
c) Renaming temporary variables:
A statement t : = b + c ( t is a temporary ) can be changed to u : = b + c (u is a new temporary) and all uses of this instance of t can be changed to u without changing the value of the basic block. Such a block is called a normal-form block.
d) Interchange of statements:
Suppose a block has the following two adjacent statements:
t1 : = b + c
t2 : = x + y
We can interchange the two statements without affecting the value of the block if and only if neither x nor y is t1 and neither b nor c is t2.
2. Algebraic transformations:
Algebraic transformations can be used to change the set of expressions computed by a basic block into an algebraically equivalent set.
Examples:
i) x : = x + 0 or x : = x * 1 can be eliminated from a basic block without changing the set of expressions it computes.
ii) The exponential statement x : = y * * 2 can be replaced by x : = y * y.
Flow Graphs
- Flow graph is a directed graph containing the flow-of-control information for the set of basic blocks making up a program.
The nodes of the flow graph are basic blocks. It has a distinguished initial node.
- E.g.: Flow graph for the vector dot product is given as follows:
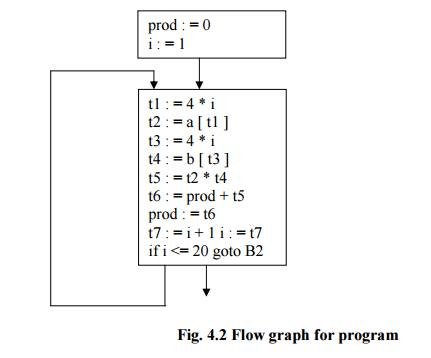
Fig. 4.2 Flow graph for program
- B1 is the initial node. B2 immediately follows B1, so there is an edge from B1 to B2. The target of jump from last statement of B1 is the first statement B2, so there is an edge from B1 (last statement) to B2 (first statement).
- B1 is the predecessor of B2, and B2 is a successor of B1.
Loops
- A loop is a collection of nodes in a flow graph such that
1. All nodes in the collection are strongly connected.
2. The collection of nodes has a unique entry.
- A loop that contains no other loops is called an inner loop.
FAQs on Basic Blocks and Flow Graphs of Code Generation -Code Generation,Computer Science and IT Engineering - Computer Science Engineering (CSE)
| 1. What are basic blocks in code generation? |  |
| 2. How are flow graphs used in code generation? |  |
| 3. What is the importance of basic blocks and flow graphs in code generation? |  |
| 4. How are basic blocks and flow graphs created during code generation? |  |
| 5. Can basic blocks and flow graphs be modified during code generation? |  |














