Converting Between Number Systems | Digital Electronics - Electrical Engineering (EE) PDF Download
It is often necessary to convert values written in one number system to another. The simplest way is to reach for your calculator or use a conversion app. from the web. That is fine, but converting a number in this way does not help you to understand the way each number system works and how different systems are related. The purpose of this module is to explain just that, and to get you to carry out some simple conversions so that you can not only convert between number systems, but also understand how the conversion process works. There are various ways to tackle conversions without a calculator; once the conversion methods are learned, the only skills needed are the ability to multiply and divide, and to add together a few numbers.
Conversion from any system to decimal
The number of values that can be expressed by a single digit in any number system is called the system radix, and any value can be expressed in terms of its system radix.
Octal to Decimal
For example the system radix of octal is 8, since any of the 8 values from 0 to 7 can be written as a single digit.
Convert 1268 to decimal.
Using the value of each column, (which in an octal integer are powers of 8) the octal value 1268 can also be written as:
(1x82) + (2x81) + (6 x 80)
As (82 = 64), (81 = 8) and (80 =1), this gives a multiplier value for each column.
Multiply the digit in each column by the column multiplier value for that column to give:
1x64 = 64 2x8 =16 6x1 = 6
Then simply add these results to give the decimal value.
64 + 16 + 6 = 8610
Therefore 1268 = 8610.
Binary to Decimal
Convert 11012 to decimal.
The same method can be used to convert binary number to decimal:
= (1x23)+(1x22)+(0x21)+(1x20)
= 8 + 4 +0 +1
= 1310
Therefore 11012 = 1310.
Hexadecimal to Decimal
Convert B2D16 to decimal.
Using the same method to convert hexadecimal to decimal.
= (Bx162)+(2x161)+(Dx160)
= (11x162)+(2x161)+(13x160)
= 2816 + 32 +13
= 286110
Therefore B2D16 = 286110.
The same method (multiplying each digit by it's column value) can be to convert any system to decimal.
Converting from Decimal to any Radix
To convert a decimal integer number (a decimal number in which any fractional part is ignored) to any other radix, all that is needed is to continually divide the number by its radix, and with each division, write down the remainder. When read from bottom to top, the remainder will be the converted result.
Decimal to Octal
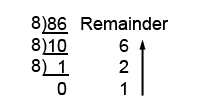
Example 1.2.2 Decimal to Octal Conversion
For example, to convert the decimal number 8610 to octal:
Divide 8610 by the system radix, which when converting to octal is 8. This gives the answer 10, with a remainder of 6.
Continue dividing the answer by 8 and writing down the remainder until the answer = 0
Now simply write out the remainders, starting from the bottom, to give 1268
Therefore 8610 = 1268
Decimal to Binary
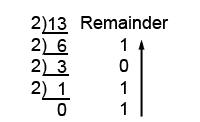
Example 1.2.1 Decimal to Binary Conversion
This process also works to convert decimal to binary, but this time the system radix is 2:
For example, to convert the decimal number 1310 to binary:
Therefore 1310 = 11012
Decimal to Hexadecimal

Example 1.2.3 Decimal to Hexadecimal Conversion
It also works to convert decimal to hexadecimal, but now the radix is 16:
As some of the remainders may be greater than 9 (and so require their alphabetic replacement), you may find it easier to use Decimal for the remainders, and then convert them to Hex.
Therefore 286110 = B2D16
Numbers with Fractions
It is very common in the decimal system to use fractions; that is any decimal number that contains a decimal point, but how can decimal numbers, such as 34.62510 be converted to binary fractions?
In electronics this is not normally done, as binary does not work well with fractions. However as fractions do exist, there has to be a way for binary to deal with them. The method used is to get rid of the radix (decimal) point by NORMALISING the decimal fraction using FLOATING POINT arithmetic. As long as the binary system keeps track of the number of places the radix point was moved during the normalisation process, it can be restored to its correct position when the result of the binary calculation is converted back to decimal for display to the user.
However, for the sake of completeness, here is a method for converting decimal fractions to binary fractions. By carefully selecting the fraction to be converted, the system works, but with many numbers the conversion introduces inaccuracies; a good reason for not using binary fractions in electronic calculations.
Converting the Decimal Integer to Binary
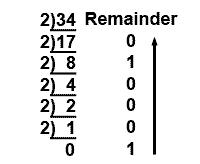
Example 1.2.4 Converting the Integer to Binary
The radix point splits the number into two parts; the part to the left of the radix point is called the INTEGER. The part to the right of the radix point is the FRACTION. A number such as 34.62510 is therefore split into 3410 (the integer), and .62510 (the fraction).
To convert such a fractional decimal number to any other radix, the method described above is used to covert the integer.
So 3410 = 1000102
Converting the Decimal Fraction to Binary

Example 1.2.5 Converting the Fraction to Binary
To convert the fraction, this must be MULTIPLIED by the radix (in this case 2 to convert to binary). Notice that with each multiplication a CARRY is generated from the third column. The Carry will be either 1 or 0 and these are written down at the left hand side of the result. However when each result is multiplied the carry is ignored (don’t multiply the carry). Each result is multiplied in this way until the result (ignoring the carry) is 000. Conversion is now complete.
For the converted value just read the carry column from top to bottom.
So 0.62510 = .1012
Therefore the complete conversion shows that 34.62510 = 100010.1012
However, with binary, there is a problem in using this method, .625 converted easily but many fractions will not. For example if you try to convert .626 using this method you would find that the binary fraction produced goes on to many, many places without a result of exactly 000 being reached.
With some decimal fractions, using the above method will produce carries with a repeating pattern of ones and zeros, indicating that the binary fraction will carry on infinitely. Many decimal fractions can therefore only be converted to binary with limited accuracy. The number of places after the radix point must be limited, to produce as accurate an approximation as required.
Quick Conversions
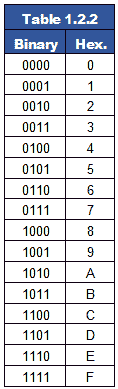
The most commonly encountered number systems are binary and hexadecimal, and a quick method for converting to decimal is to use a simple table showing the column weights, as shown in Tables 1.2.1a and 1.2.1b.
Converting Binary to Decimal
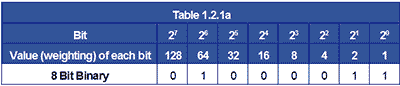
To convert from binary to decimal, write down the binary number giving each bit its correct ‘weighting’ i.e. the value of the columns, starting with a value of one for the right hand (least significant) bit. Giving each bit twice the value of the previous bit as you move left.
Example:
To convert the binary number 010000112 to decimal. Write down the binary number and assign a ‘weighting’ to each bit as in Table 1.2.1a
Now simply add up the values of each column containing a 1 bit, ignoring any columns containing 0.
Applying the appropriate weighting to 01000011 gives 64 + 2 + 1 = 67
Therefore: 010000112 = 6710
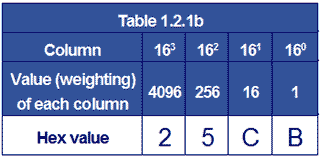
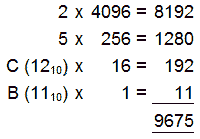
Converting Hexadecimal to Decimal
A similar method can be used to quickly convert hexadecimal to decimal, using Table 1.2.1b
The hexadecimal digits are entered in the bottom row and then multiplied by the weighting value for that column.
Adding the values for each column gives the decimal value.
Therefore: 25CB16 = 967510
Binary and Hexadecimal
Converting between binary and hexadecimal is a much simpler process; hexadecimal is really just a system for displaying binary in a more readable form.
Binary is normally divided into Bytes (of 8 bits) it is convenient for machines but quite difficult for humans to read accurately. Hexadecimal groups each 8-bit byte into two 4-bit nibbles, and assigns a value of between 0 and 15 to each nibble. Therefore each hexadecimal digit (also worth 0 to 15) can directly represent one binary nibble. This reduces the eight bits of binary to just two hexadecimal characters.
For example:
111010012 is split into 2 nibbles 11102 and 10012 then each nibble is assigned a hexadecimal value between 0 and F.
The bits in the most significant nibble (11102) add up to 8+4+2+0 = 1410 = E16
The bits in the least significant nibble (10012) add up to 8+0+0+1 = 910 = 916
Therefore 111010012 = E916
Converting hexadecimal to binary of course simply reverses this process.
Hexadecimal to Binary Number System
To convert from Hexadecimal to Binary, write the 4-bit binary equivalent of hexadecimal.
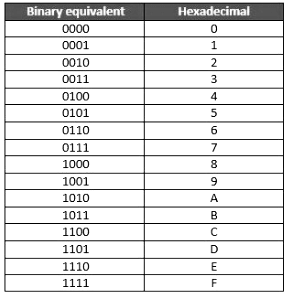
Example
(3A)16 = (00111010)2
Binary to Hexadecimal Number System
To convert from Binary to Hexadecimal, start grouping the bits in groups of 4 from the right-end and write the equivalent hexadecimal for the 4-bit binary. Add extra 0’s on the left to adjust the groups.
Example
1111011011
0011 1101 1011
(001111011011)2 = (3DB)16
Signed Binary Notation
All the binary arithmetic problems looked at in Module 1.3 used only POSITIVE numbers. The reason for this is that it is not possible in PURE binary to signify whether a number is positive or negative. This of course would present a problem in any but the simplest of arithmetic.
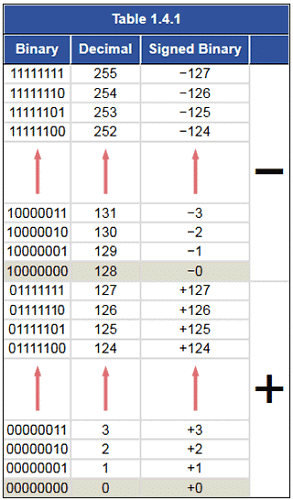
There are a number of ways in which binary numbers can represent both positive and negative values, 8 bit systems for example normally use one bit of the byte to represent either + or − and the remaining 7 bits to give the value. One of the simplest of these systems is SIGNED BINARY, also often called ‘Sign and Magnitude’, which exists in several similar versions, but is commonly an 8 bit system that uses the most significant bit (msb) to indicate a positive or a negative value. By convention, a 0 in this position indicates that the number given by the remaining 7 bits is positive, and a most significant bit of 1 indicates that the number is negative.
For example:
+4510 in signed binary is (0)01011012
-4510 in signed binary is (1)01011012
Note:
The brackets around the msb (the sign bit) are included here for clarity but brackets are not normally used. Because only 7 bits are used for the actual number, the values the system can represent range from is −12710 or 111111112, to +12710.
A comparison between signed binary, pure binary and decimal numbers is shown in Table 1.4.1. Notice that in the signed binary representation of positive numbers between +010 and +12710, all the positive values are just the same as in pure binary. However the pure binary values equivalents of +12810 to +25510 are now considered to represent negative values −0 to −127.
This also means that 010 can be represented by 000000002 (which is also 0 in pure binary and in decimal) and by 100000002 (which is equivalent to 128 in pure binary and in decimal).
Signed Binary Arithmetic

Because the signed binary system now contains both positive and negative values, calculation performed with signed binary arithmetic should be more flexible. Subtraction now becomes possible by adding a negative number to a positive number, without the problems of borrow and payback described in Fig. 1.4.1 Adding Positive Number Systems Module 1.3. However there are still problems. Look at the two Numbers in Signed Binary examples illustrated in Fig. 1.4.1 and 1.4.2, using signed binary notation. Z
In Fig. 1.4.1 two positive (msb = 0) numbers are added and the correct answer is obtained. This is really no different to adding two numbers in pure binary.
In Fig. 1.4.2 however, the negative number −5 is added to +7, the same action in fact as SUBTRACTING 5 from 7, which means that subtraction should be possible by merely adding a negative number to a positive number. Although this principle works in the decimal version the result using signed binary is 100011002 or −1210 which of course is wrong, the result of 7 − 5 should be +2.
 Fig. 1.4.2 Adding Positive & Negative Numbers in Signed Binary
Fig. 1.4.2 Adding Positive & Negative Numbers in Signed Binary
Although signed binary can represent positive and negative numbers, if it is used for calculations, some special action would need to be taken, depending on the sign of the numbers used, and how the two values for 0 are handled, to obtain the correct result. Whilst signed binary does solve the problem of REPRESENTING positive and negative numbers in binary, and to some extent carrying out binary arithmetic, there are better sign and magnitude systems for performing binary arithmetic. These systems are the ONES COMPLEMENT and TWOS COMPLEMENT systems, which are described in Number Systems.
|
115 videos|71 docs|58 tests
|
FAQs on Converting Between Number Systems - Digital Electronics - Electrical Engineering (EE)
| 1. How do you convert a number from any system to decimal? |  |
| 2. How can you convert a decimal number to any radix? |  |
| 3. How do you convert numbers with fractions between different number systems? |  |
| 4. What are some quick methods for converting between binary and hexadecimal? |  |
| 5. How do you represent negative numbers in the signed binary notation? |  |

|
Explore Courses for Electrical Engineering (EE) exam
|

|