Test: MCQs (One or More Correct Option): Complex Numbers | JEE Advanced - JEE MCQ
10 Questions MCQ Test - Test: MCQs (One or More Correct Option): Complex Numbers | JEE Advanced
If z1 = a + ib and z2 = c + id are complex numbers such that |z1| = |z2|=1 and Re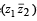 =0, then the pair of complex numbers w1 = a + ic and w2 = b + id satisfies – (1985 - 2 Marks)
=0, then the pair of complex numbers w1 = a + ic and w2 = b + id satisfies – (1985 - 2 Marks)
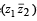 =0, then the pair of complex numbers w1 = a + ic and w2 = b + id satisfies – (1985 - 2 Marks)
=0, then the pair of complex numbers w1 = a + ic and w2 = b + id satisfies – (1985 - 2 Marks)Let z1 and z2 be complex numbers such that z1 ≠ z2 and |z1| = |z2| . If z1 has positive real part and z2 has negative imaginary part, then may be (1986 - 2 Marks)
If z1 and z2 are two nonzero complex numbers such that |z1 + z2|=|z1|+ |z2|, then Arg z1 - Argg z2 is equal to (1987 - 2 Marks)
The value of 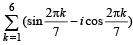 is (1987 - 2 Marks)
is (1987 - 2 Marks)
If ω is an imaginary cube root of unity, then (1 + ω – ω2)7 equals (1998 - 2 Marks)
The value of the sum 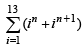 , where i =
, where i =  , equals (1998 - 2 Marks)
, equals (1998 - 2 Marks)
If 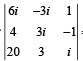 = x + iy, then (1998 - 2 Marks)
= x + iy, then (1998 - 2 Marks)
Let z1 an d z2 be two distinct complex numbers an d let z = (1 – t) z1 + tz2 for some real number t with 0 < t < 1. If Arg (w) denotes the principal argument of a non-zero complex number w, then (2010)
Let w =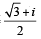 and P = {wn : n = 1, 2, 3, ...}. Further H1 =
and P = {wn : n = 1, 2, 3, ...}. Further H1 =
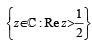 and H2
and H2 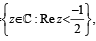 where c is the set of all complex numbers. If z1∈ P∩H1, z2 ∈ P∩H2 and O represents the origin, then ∠z1Oz2 = (JEE Adv. 2013)
where c is the set of all complex numbers. If z1∈ P∩H1, z2 ∈ P∩H2 and O represents the origin, then ∠z1Oz2 = (JEE Adv. 2013)
Let a, b ∈ R and a2 + b2 ≠ 0.
Suppose 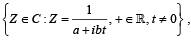 where
where
i =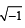 . If z = x+ iy and z ∈ S, then (x, y) lies on (JEE Adv. 2016)
. If z = x+ iy and z ∈ S, then (x, y) lies on (JEE Adv. 2016)


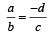 = α(say) ....(2)
= α(say) ....(2)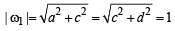
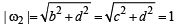
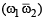 = ab + cd = (bα) b + c (-cα)
= ab + cd = (bα) b + c (-cα)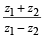
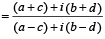
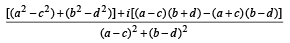
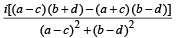 [Using (1)]
[Using (1)]
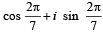
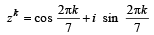
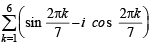
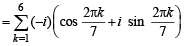
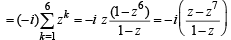
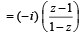 = [Using z7 = cos 2π + i sin 2π = 1]
= [Using z7 = cos 2π + i sin 2π = 1]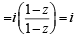
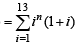
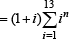
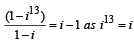
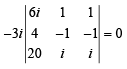 (∵ C2 ≡ C3)
(∵ C2 ≡ C3)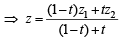
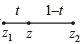
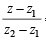 = t = purely real number
= t = purely real number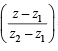 = 0 ⇒ arg(z - z) = arg(z-z)
= 0 ⇒ arg(z - z) = arg(z-z)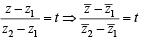

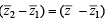 (z2 –z1)
(z2 –z1)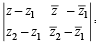 = 0
= 0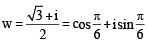
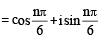
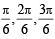 and so on.
and so on.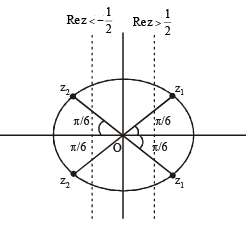

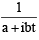 = x + iy
= x + iy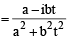
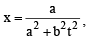
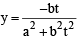
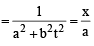
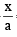
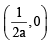 and radius
and radius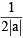 irrespective of ‘a’ +ve or –ve
irrespective of ‘a’ +ve or –ve
















