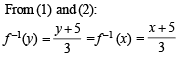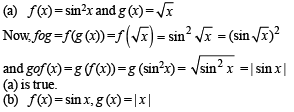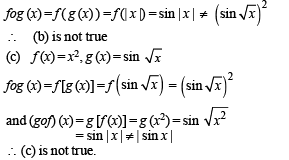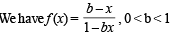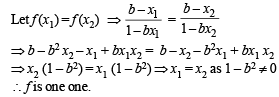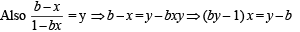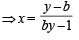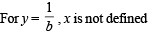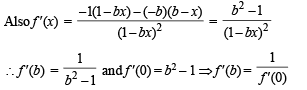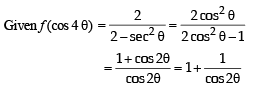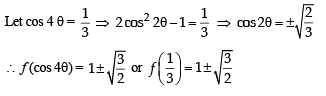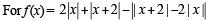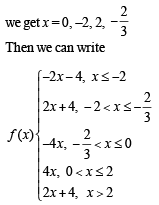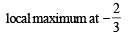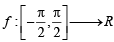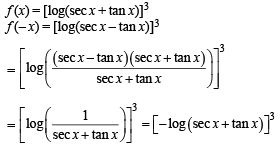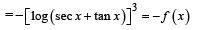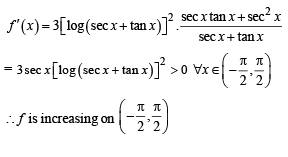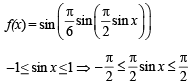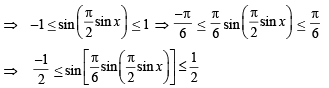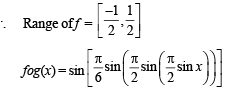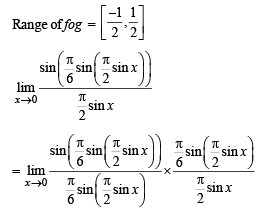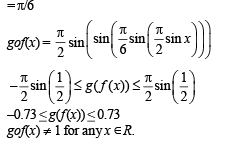Test: JEE Advanced (One or More Correct Option): Functions - JEE MCQ
11 Questions MCQ Test - Test: JEE Advanced (One or More Correct Option): Functions
Let g (x) be a function defined on [– 1, 1]. If the area of the equilateral triangle with two of its vertices at (0,0) and 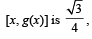 then the function g(x) is
then the function g(x) is
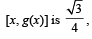 then the function g(x) is
then the function g(x) is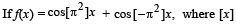 stands for the greatest integer function, then
stands for the greatest integer function, then
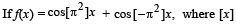 stands for the greatest integer function, then
stands for the greatest integer function, thenIf f(x) = 3x – 5, then f–1(x)
If g (f(x)) = | sin x | and f (g(x)) = (sin √x)2, then
Let f : (0, 1) → R be defined by 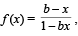 where b is a constant such that 0 < b < 1. Then
where b is a constant such that 0 < b < 1. Then
Let f : (–1, 1) ⇒ IR be such that 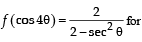
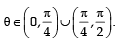 Then the value (s) of
Then the value (s) of 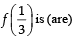
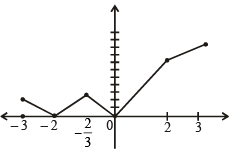
The function f(x) = 2|x| + |x + 2| – | |x + 2| – 2 |x| has a local minimum or a local maximum at x =
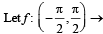 R be given by f (x) = (log(sec x + tan x))3.
R be given by f (x) = (log(sec x + tan x))3.
Then
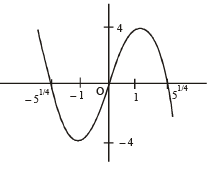
Let a ∈ R and let f : R → R be given by f (x) = x5 – 5x + a. Then
Let 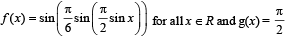 sin x for all x ∈ R. Let (fog)(x) denote f(g(x)) and (gof)(x) denote g(f(x)). Then which of the following is (are) true?
sin x for all x ∈ R. Let (fog)(x) denote f(g(x)) and (gof)(x) denote g(f(x)). Then which of the following is (are) true?


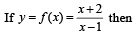
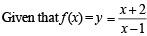
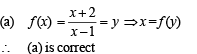
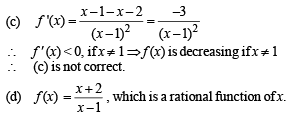
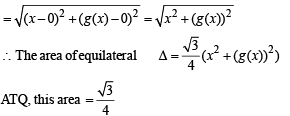
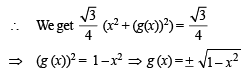

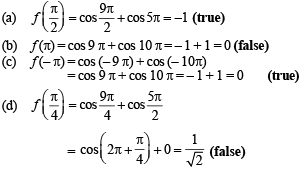
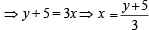 ...(1)
...(1)