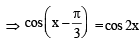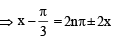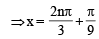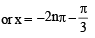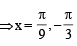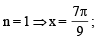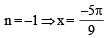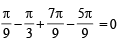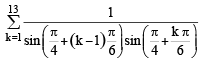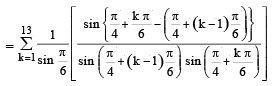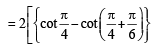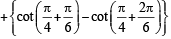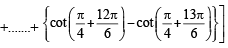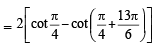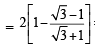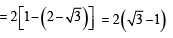JEE Advanced (Single Correct MCQs): Trigonometric Functions & Equations - JEE MCQ
29 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Trigonometric Functions & Equations
If tanθ = - 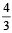 , then sinθ is (1979)
, then sinθ is (1979)
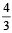 , then sinθ is (1979)
, then sinθ is (1979)If α + β + γ = 2π, then (1979)
Given A = sin2θ + cos4θ, then for all real values of θ (1980)
The equation 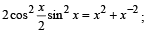
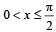 has
has
The general solution of the trigonometric equation sin x+cos x = 1 is given by : (1981 - 2 Marks)
The value of th e expression 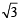 cos ec 20° – sec 20° is equal to (1988 - 2 Marks)
cos ec 20° – sec 20° is equal to (1988 - 2 Marks)
The general solution of sin x – 3 sin 2x + sin 3x = cos x – 3 cos 2x + cos 3x is (1989 - 2 Marks)
The equation (cos p – 1) x 2 + (cos p)x + sin p = 0 In the variable x, has real roots. Then p can take any value in the interval (1990 - 2 Marks)
Number of solutions of the equation tan x + sec x= 2 cosx lying in the interval [0, 2π] is : (1993)
Let 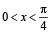 then (sec2x – tan2x) equals (1994)
then (sec2x – tan2x) equals (1994)
Let n be a positive in teger such that 
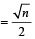 Then (1994)
Then (1994)
If ω is an imaginary cube root of unity then the value of 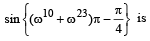 (1994)
(1994)
3 (sin x - cosx)4 + 6 (sin x + cosx)2 + 4 (sin6 x + cos6x) = (1995S)
The general values of θ satisfying the equation 2sin2θ – 3sinθ – 2 = 0 is (1995S)
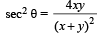 is true if and only if (1996 - 1 Mark)
is true if and only if (1996 - 1 Mark)
In a triangle PQR, ∠R =π /2 . If tan (P/2) and tan (Q/2) are the roots of the equation ax2 + bx + c = 0 (a ≠ 0) then. (1999 - 2 Marks)
Let f (θ) = sinθ(sinθ + sin3θ). Then f(θ) is (2000S)
The number of distinct real roots of 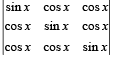 = 0 in the interval
= 0 in the interval 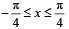 is (2001S)
is (2001S)
The maximum value of (cot α1). (cot α2 ) .... (cot αn), under the restrictions 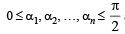 and
and 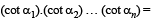 1 is (2001S)
1 is (2001S)
If α + β = π/2 and β + γ = α, then tan α equals (2001S)
The number of integral values of k for which the equation 7 cos x + 5 sin x = 2k + 1 has a solution is (2002S)
Given both θ and φ are acute an gles and 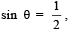
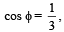 then the value of θ + φ belongs to (2004S)
then the value of θ + φ belongs to (2004S)
cos(α – β) = 1 an d cos(α + β) = 1/e where α, β ∈ [–π, π].Pairs of α, β which satisfy both the equations is/are (2005S)
The values of θ ∈ (0, 2π) for which 2 sin2θ – 5 sinθ + 2 > 0, are (2006 - 3M, –1)
Let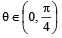 and
and 
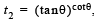
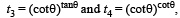 then (2006 - 3M, –1)
then (2006 - 3M, –1)
The number of solutions of the pair of equations
2sin2θ – cos2θ = 0
2cos2θ – 3sinθ = 0
in the interval [0, 2π] is (2007 - 3 Marks)
For x ∈( 0,p ) , the equation sinx + 2sin 2x – sin 3x = 3 has (JEE Adv. 2014)
Let 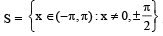 The sum of all distinct solutions of the equation
The sum of all distinct solutions of the equation
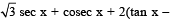 cot x) = 0 in the set S is equal to (JEE Adv. 2016)
cot x) = 0 in the set S is equal to (JEE Adv. 2016)
The value of 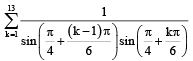 is equal to (JEE Adv. 2016)
is equal to (JEE Adv. 2016)


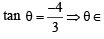 II quad or IV quad
II quad or IV quad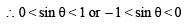
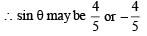
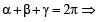
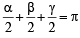
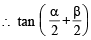
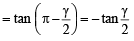
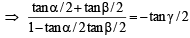

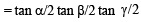

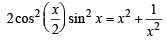 where
where 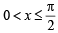

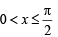
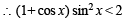
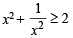
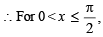
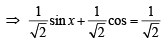
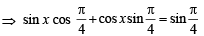

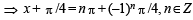 (the set of integers)
(the set of integers)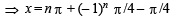
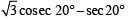
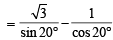
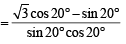
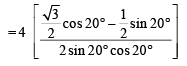
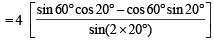
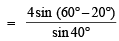

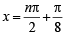
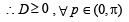
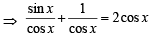
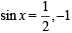

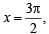 given eq. is not defined,
given eq. is not defined,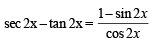
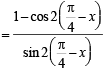
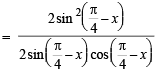
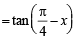
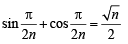
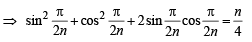
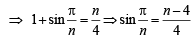
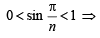
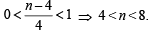
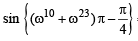
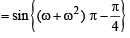
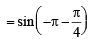
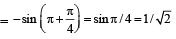
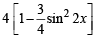
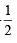 [∴ sinθ - 2=0 is not possible]
[∴ sinθ - 2=0 is not possible]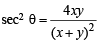

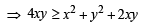
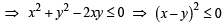
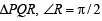

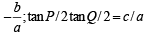
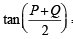
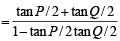
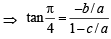
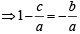
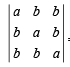 = 0 Operating C2 – C1; C3 – C2 we get
= 0 Operating C2 – C1; C3 – C2 we get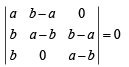
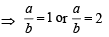
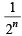 [sin 2α1 sin 2α2 .... sin2 αn ]
[sin 2α1 sin 2α2 .... sin2 αn ]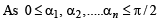
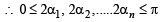
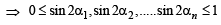
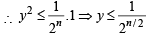
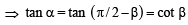
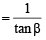
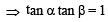
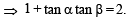
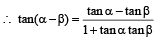
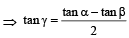
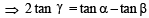
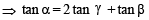
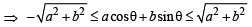
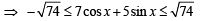
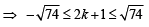
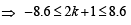
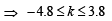
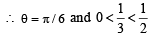
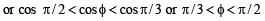
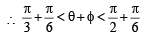
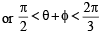
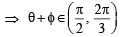
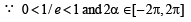
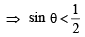
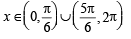
 tanθ < 1 and cotθ >1
tanθ < 1 and cotθ >1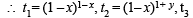
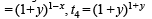

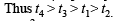
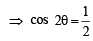
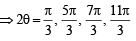
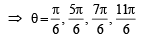 ....(1)
....(1)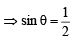
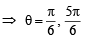 .... (2), where q ∈ [0, 2π]
.... (2), where q ∈ [0, 2π]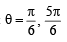
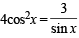
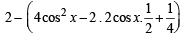
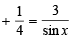

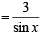
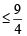 and RHS ≥ 3
and RHS ≥ 3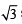 sec x + cosec x + 2 (tan x – cot x) = 0
sec x + cosec x + 2 (tan x – cot x) = 0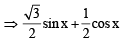 = cos2x – sin2 x
= cos2x – sin2 x