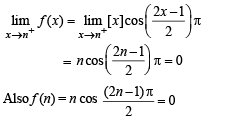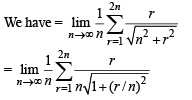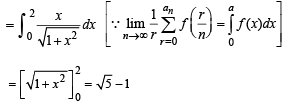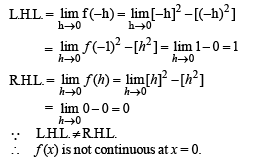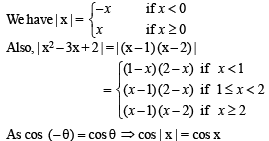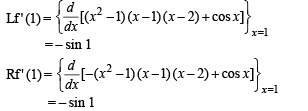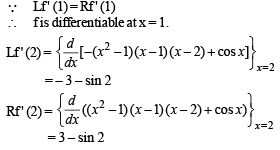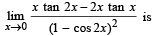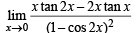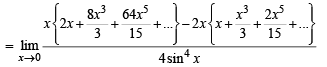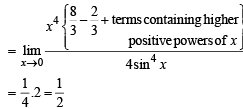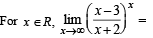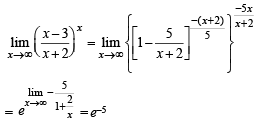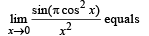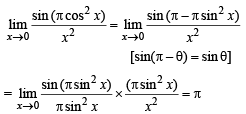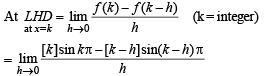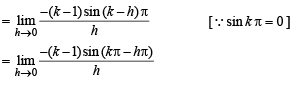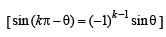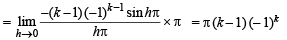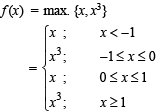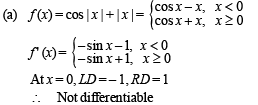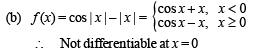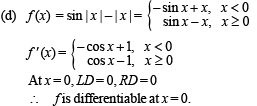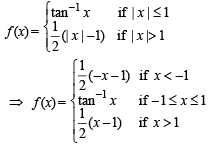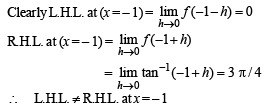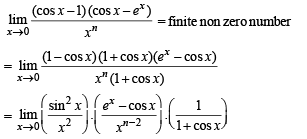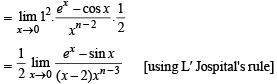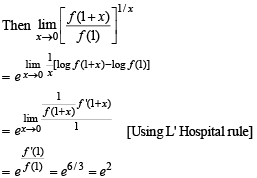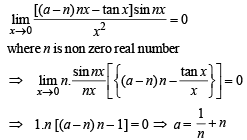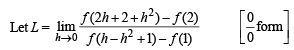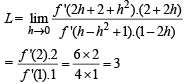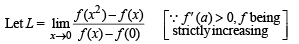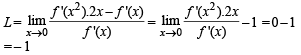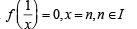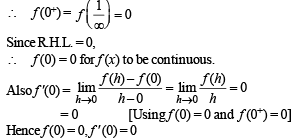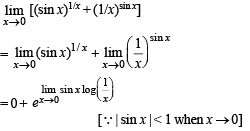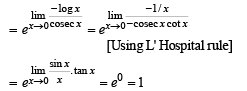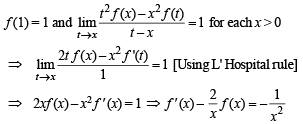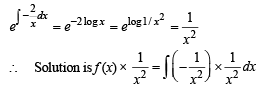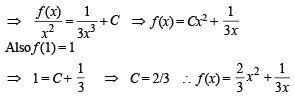JEE Advanced (Single Correct MCQs): Limits, Continuity and Differentiability - JEE MCQ
30 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Limits, Continuity and Differentiability
For a real number y, let [y] denotes the greatest integer less than or equal to y : Then the function 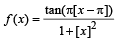
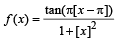
There exist a function f (x), satisfying f (0) = 1, f '(0) = –1, f (x) > 0 for all x, and
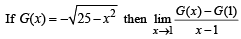 has the value
has the value
If f (a) = 2, f ' (a) = 1 , g (a) = -1 , g ' (a) = 2 , then the value of 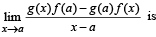
The function 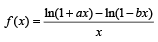 is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0, is
is not defined at x = 0. The value which should be assigned to f at x = 0 so that it is continuous at x = 0, is
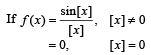
Where [x] denotes the greatest integer less than or equal to x. then 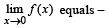
Let f : R → R be a differentiable function and f (1) = 4. Then the value of 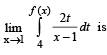
Let [.] den ote th e greatest integer function and f (x) = [tan 2x], then:
The function 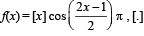 denotes the greatest integer function, is discontinuous at
denotes the greatest integer function, is discontinuous at
The function f(x) = [x]2 – [x2] (where [y] is the greatest integer less than or equal to y), is discontinuous at
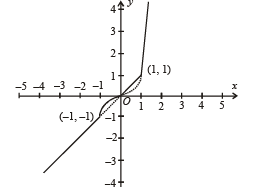
The function f (x) = (x2 - 1) | x2 - 3x + 2 |+cos (|x|) is NOT differentiable at
The left-hand derivative of f(x) = [x] sin(p x) at x = k, k an integer, is
Let f : R → R be a function defined by f (x) = max {x, x3}. The set of all points where f (x) is NOT differentiable is
Which of the following functions is differentiable at x = 0?
The domain of the derivative of the function
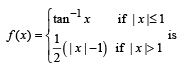
The integer n for which 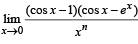 is a finite non-zero number is
is a finite non-zero number is
Let f : R → R be such that f (1) = 3 and f '(1) = 6. Then 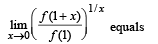
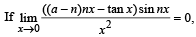 where n is nonzero real number, then a is equal to
where n is nonzero real number, then a is equal to
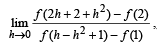 given that f ' (2) = 6 and f '(1) = 4
given that f ' (2) = 6 and f '(1) = 4
If (x) is differentiable and strictly increasing function, then the value of 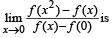
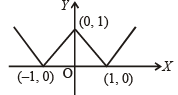
The function given by y = ||x| – 1| is differentiable for all real numbers except th e points
If f (x) is continuous an d differ en tiable function and 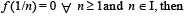
The value of 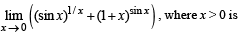
Let f (x) be differentiable on the interval (0, ∞) such that 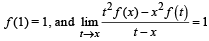 for each x > 0. Then f (x) is
for each x > 0. Then f (x) is


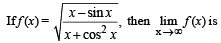
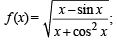
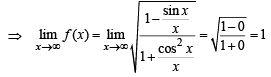
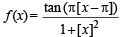
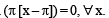

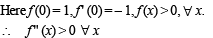
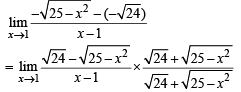
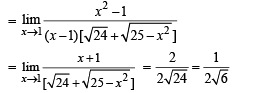
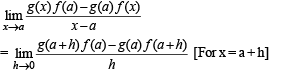
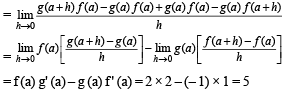
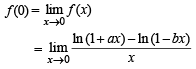
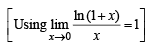
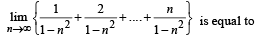


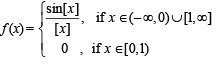
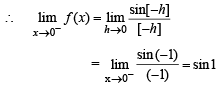
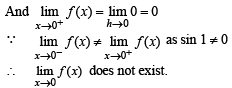
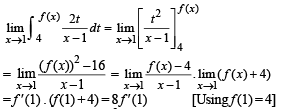
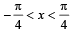
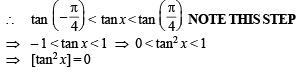
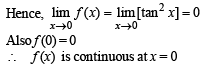
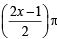 are continuous.
are continuous.