JEE Advanced (Single Correct MCQs): Permutations and Combinations - JEE MCQ
15 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Permutations and Combinations
nCr–1 = 36, nCr = 84 and nCr + 1 = 126, then r is : (1979)
Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are (1982 - 2 Marks)
The value of the expression 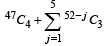 is equal to (1982 - 2 Marks)
is equal to (1982 - 2 Marks)
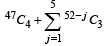 is equal to (1982 - 2 Marks)
is equal to (1982 - 2 Marks)Eight chairs are numbered 1 to 8. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 ; and then the men select the chairs from amongst the remaining. The number of possible arrangements is (1982 - 2 Marks)
A five-digit numbers divisible by 3 is to be formed using the numerals 0, 1, 2, 3, 4 and 5, without repetition. The total number of ways this can be done is (1989 - 2 Marks)
How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions ? (2000S)
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn + 1 - Tn = 21, then n equals (2001S)
The number of arrangements of the letters of the word BANANA in which the two N's do not appear adjacently is (2002S)
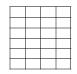
A rectangle with sides of length (2m – 1) an d (2n – 1) units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side length s is (2005S)
If the LCM of p, q is r2t4s2, where r, s, t are prime numbers and p, q are the positive integers then the number of ordered pair (p, q) is (2006 - 3M, –1)
The letters of the word COCHIN are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word COCHIN is (2007 -3 marks)
The number of seven digit i ntegers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is (2009)
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is (2012)
Six cards and six envelopes are numbered 1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover the card numbered 1 is always placed in envelope numbered 2. Then the number of ways it can be done is (JEE Adv. 2014)
A debate club consists of 6 girls and 4 boys. A team of 4 members is to be selected from this club including the selection of a captain (from among these 4 memoers) for the team. If the team has to include at most one boy, then the number of ways of selecting the team is (JEE Adv. 2016)


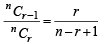
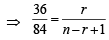
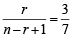
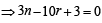 ....(1)
....(1)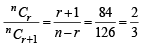
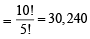

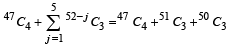
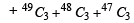
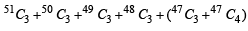
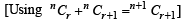
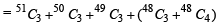
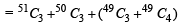
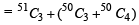
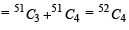
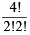 = 6 ways.
= 6 ways.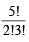 = 10ways.
= 10ways.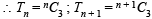
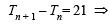
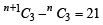
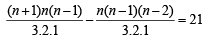
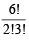 = 60 Number of words in which 2 N’s come together is
= 60 Number of words in which 2 N’s come together is 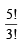 = 20
= 20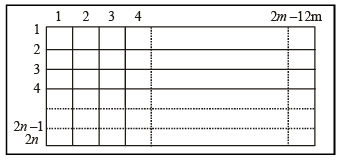
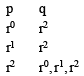
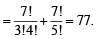
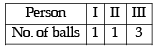
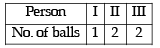
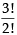 ways.
ways.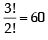
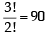
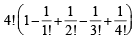 = 9 ways
= 9 ways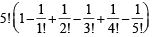 = 44 ways
= 44 ways










