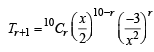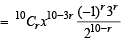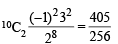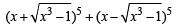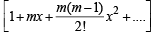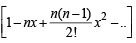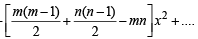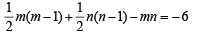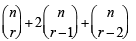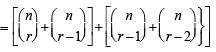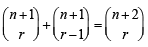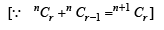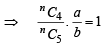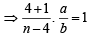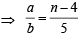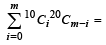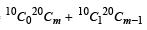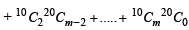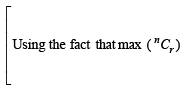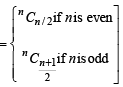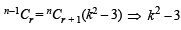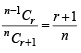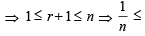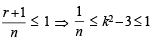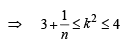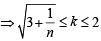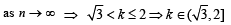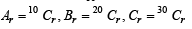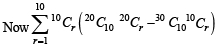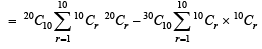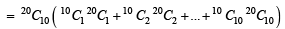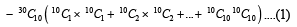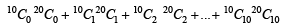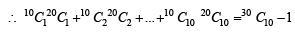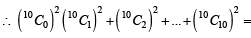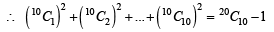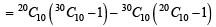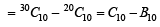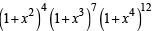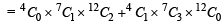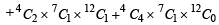Test: Single Correct MCQs: Mathematical Induction and Binomial Theorem | JEE Advanced - JEE MCQ
12 Questions MCQ Test - Test: Single Correct MCQs: Mathematical Induction and Binomial Theorem | JEE Advanced
Given positive integers r > 1, n >2 and that the coefficient of (3r)th and (r + 2)th terms in the binomial expansion of (1+ x)2n are equal . Then (1983 - 1 Mark)
The coefficient of x4 in 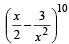 is (1983 - 1 Mark)
is (1983 - 1 Mark)
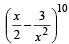 is (1983 - 1 Mark)
is (1983 - 1 Mark)The expression 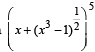
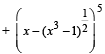 is a polynomial of degree (1992 - 2 Marks)
is a polynomial of degree (1992 - 2 Marks)
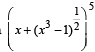
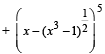 is a polynomial of degree (1992 - 2 Marks)
is a polynomial of degree (1992 - 2 Marks)If in the expansion of (1 + x)m (1 – x)n, the coefficients of x and x2 are 3 and – 6 respectively, then m is (1999 - 2 Marks)
For 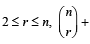
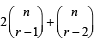 (2000S)
(2000S)
In the binomial expansion of (a - b)n, n ≥ 5, the sum of the 5th and 6th terms is zero. Then a/b equals (2001S)
The sum 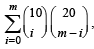 (where
(where 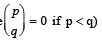 is maximum when m is (2002S)
is maximum when m is (2002S)
Coefficient of t24 in (1 +t2)12 (1+t12) (1 + t24) is (2003S)
If n–1Cr = (k2 – 3) nCr +1, then k ∈ (2004S)
The value of 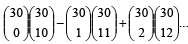
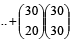 is where
is where 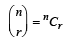 (2005S)
(2005S)
For r = 0, 1, …, 10, let Ar, Br and Cr denote, respectively, the coefficient of xr in the expansions of (1 + x)10 , (2010)
(1 + x)20 and (1 + x)30. Then 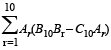 is equal to
is equal to
Coefficient of x11 in the expansion of (1 + x2)4(1 + x3)7 (1 + x4)12 is (JEE Adv. 2014)


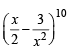 is
is