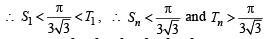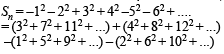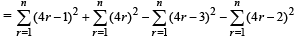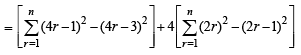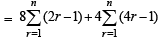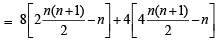Test: MCQs (One or More Correct Option): Sequences and Series | JEE Advanced - JEE MCQ
9 Questions MCQ Test - Test: MCQs (One or More Correct Option): Sequences and Series | JEE Advanced
If the first and the (2n – 1)st terms of an A.P., a G.P. and an H.P. are equal and their n-th terms are a, b and c respectively, th en (1988 - 2 Marks)
For 0 < φ < π/2, if 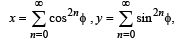
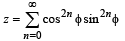 then: (1993 - 2 Marks)
then: (1993 - 2 Marks)
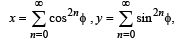
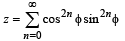 then: (1993 - 2 Marks)
then: (1993 - 2 Marks)Let n be an odd integer. If 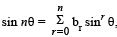 for every value of q, then (1998 - 2 Marks)
for every value of q, then (1998 - 2 Marks)
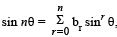 for every value of q, then (1998 - 2 Marks)
for every value of q, then (1998 - 2 Marks)Let Tr be the rth term of an A.P., for r = 1, 2, 3, .... If for some positive integers m, n we have 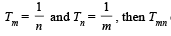 equals (1998 - 2 Marks)
equals (1998 - 2 Marks)
If x > 1, y > 1, z > 1 are in G.P., then 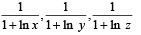 are in (1998 - 2 Marks)
are in (1998 - 2 Marks)
For a positive integer n, let 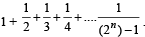 . Then (1999 - 3 Marks)
. Then (1999 - 3 Marks)
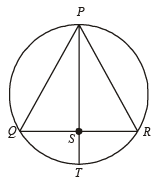
A straight line through the vertex P of a triangle PQR intersects the side QR at the point S and the circumcircle of the triangle PQR at the point T. If S is not the centre of the circumcircle, then (2008)
Let 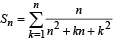
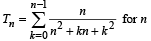 = 1, 2, 3, ............ Then, (2008)
= 1, 2, 3, ............ Then, (2008)
Let 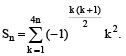 Then Sn can take value(s) (JEE Adv. 2013)
Then Sn can take value(s) (JEE Adv. 2013)


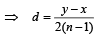
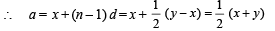 ....(1)
....(1)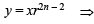
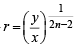
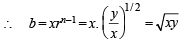 ....(2)
....(2)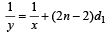
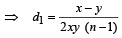
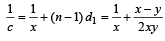
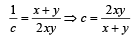 ....(3)
....(3)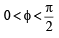
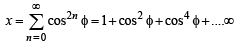
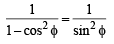 ....(1)
....(1)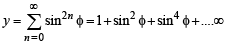
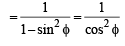 ....(2)
....(2)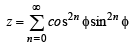
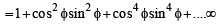
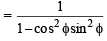 ...(3)
...(3)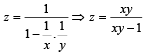
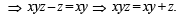
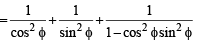
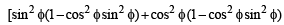
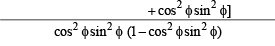
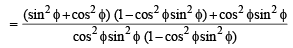
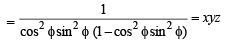

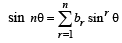
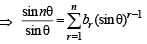
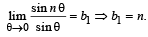

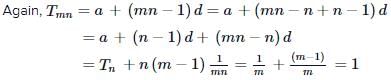
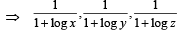 will be in H.P..
will be in H.P..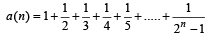
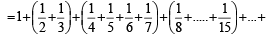
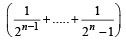
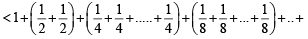
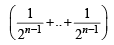
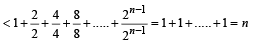
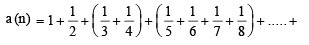
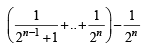
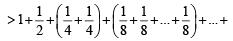
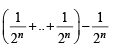
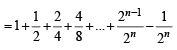
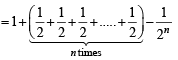
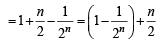
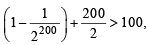
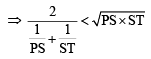

 [using eqn (1)] ...(2)
[using eqn (1)] ...(2)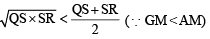
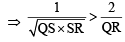
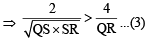
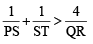
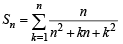
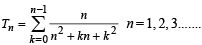
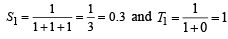
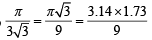 = 0.34 × 1.73 = 0.58
= 0.34 × 1.73 = 0.58