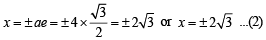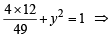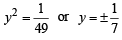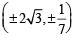JEE Advanced (Single Correct MCQs): Conic Sections - JEE MCQ
30 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Conic Sections
The equation 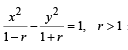 represents(1981 - 2 Marks)
represents(1981 - 2 Marks)
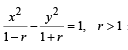 represents(1981 - 2 Marks)
represents(1981 - 2 Marks)Each of the four inequalties given below defines a region in the xy plane. One of these four regions does not have the following property. For any two points (x1, y1) and (x2, y2) in th e region , the point 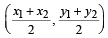 is also in the region. The inequality defining this region is (1981 - 2 Marks)
is also in the region. The inequality defining this region is (1981 - 2 Marks)
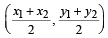 is also in the region. The inequality defining this region is (1981 - 2 Marks)
is also in the region. The inequality defining this region is (1981 - 2 Marks)The equation 2x2 + 3y2 – 8x – 18y + 35 = k represents (1994)
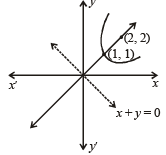
Let E be the ellipse 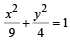 and C be the circle x2 + y2 = 9. Let P and Q be the points (1, 2) and (2, 1) respectively. Then (1994)
and C be the circle x2 + y2 = 9. Let P and Q be the points (1, 2) and (2, 1) respectively. Then (1994)
Consider a circle with its centre lying on the focus of the parabola y2 = 2px such that it touches the directrix of the parabola. Then a point of intersection of the circle and parabola is (1995S)
The radius of the circle passing through the foci of theellipse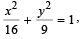 and having its centre at (0, 3) is (1995S)
and having its centre at (0, 3) is (1995S)
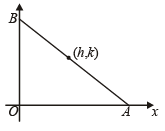
Let P (a secθ, b tanθ) and Q (a secφ, b tanφ), where q + f = π/ 2, be two points on the hyperbola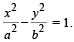 If (h, k) is the point of intersection of the normals at P and Q, then k is equal to (1999 - 2 Marks)
If (h, k) is the point of intersection of the normals at P and Q, then k is equal to (1999 - 2 Marks)
If x = 9 is the chord of contact of the hyperbola x2 – y2 = 9, then the equation of the corresponding pair of tangents is (1999 - 2 Marks)
Th e curve described par ametr ically by x = t2 + t + 1, y = t2 – t + 1 represents (1999 - 2 Marks)
If x + y = k is normal to y2 = 12 x, then k is (2000S)
If the line x – 1 = 0 is the directrix of the parabola y2 – kx + 8 = 0, then one of the values of k is (2000S)
The equation of the common tangent touching the circle (x -3)2 + y2 = 9 and the parabola y2 = 4x above the x-axis is (2001S)
The equation of the directrix of the parabola y2 + 4y + 4x + 2 = 0 is (2001S)
If a > 2b > 0 then the positive value of m for which 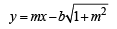 is a common tangent to x2 + y2 = b2 and (x – a)2 + y2 = b2 is (2002S)
is a common tangent to x2 + y2 = b2 and (x – a)2 + y2 = b2 is (2002S)
The locus of the mid-point of the line segment joining the focus to a moving point on the parabola y2 = 4ax is another parabola with directrix (2002S)
The equation of the common tangent to the curves y2 = 8x and xy = –1 is (2002S)
The area of the quadrilateral formed by the tangents at the end points of latus rectum to the ellipse 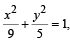 is
is
The focal chord to y2 = 16x is tangent to (x – 6)2 + y2 = 2, then the possible values of the slope of this chord, are (2003S)
For hyperbola 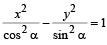 which of the following remains constant with change in ‘α’ (2003S)
which of the following remains constant with change in ‘α’ (2003S)
If tangents are drawn to the ellipse x2 + 2y2 = 2, then the locus of the mid-point of the intercept made by the tangents between the coordinate axes is (2004S)
The angle between the tangents drawn from the point (1, 4) to the parabola y2 = 4x is (2004S)
If the line 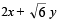 = 2 touches the hyperbola x2 – 2y2 = 4, then the point of contact is (2004S)
= 2 touches the hyperbola x2 – 2y2 = 4, then the point of contact is (2004S)
The minimum area of triangle formed by the tangent to the 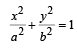 & coordinate axes is (2005S)
& coordinate axes is (2005S)
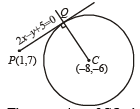
Tangent to the curve y = x2 + 6 at a point (1, 7) touches the circle x2 + y2 + 16x + 12y + c = 0 at a point Q. Then the coordinates of Q are (2005S)
The axis of a parabola is along the line y = x and the distances of its vertex and focus from origin are 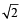 and
and 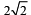 respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (2006 - 3M, –1)
respectively. If vertex and focus both lie in the first quadrant, then the equation of the parabola is (2006 - 3M, –1)
A hyperbola, having the transverse axis of length 2 sinθ, is confocal with the ellipse 3x2 + 4y2 = 12. Then its equation is (2007 - 3 marks)
Let a and b be non-zero real numbers. Then, the equation (ax2 + by2 + c) (x2 – 5xy + 6y2) = 0 represents (2008)
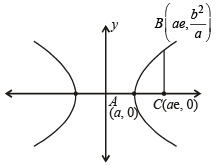
Consider a branch of the hyperbola 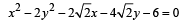 with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of the triangle ABC is (2008)
with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of the triangle ABC is (2008)
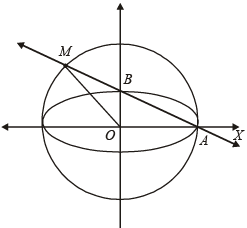
The line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x2 + 9y2 = 9 meets its auxiliary circle at the point M. Then the area of the triangle with vertices at A, M and the origin O is (2009)
The normal at a point P on the ellipse x2 + 4y2 = 16 meets the x - axis at Q. If M is the mid point of the line segment PQ, then the locus of M intersects the latus rectums of the given ellipse at the points (2009)


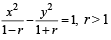
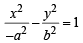
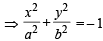
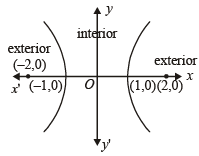

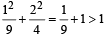 and
and 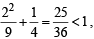 P lies outside E and Q lies inside E. Thus P lies inside C but outside E.
P lies outside E and Q lies inside E. Thus P lies inside C but outside E. and directrix
and directrix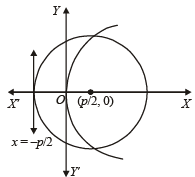
 and radius
and radius 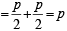
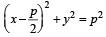
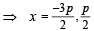
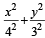 = 1, a = 4, b = 3
= 1, a = 4, b = 3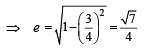
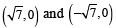
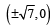 , therefore radius of circle =
, therefore radius of circle = 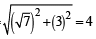
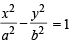
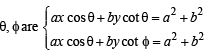
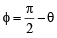 and these pass through (h, k)
and these pass through (h, k)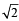 ) and (9, –6
) and (9, –6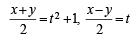 (Adding and subtracting values of x and y)
(Adding and subtracting values of x and y)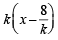

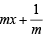
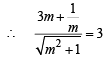
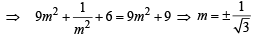
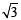 + 3=0 and
+ 3=0 and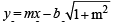 ...(1)
...(1)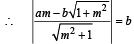
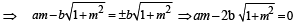
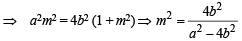
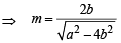 (∵ m > 0)
(∵ m > 0)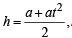 k = at
k = at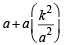
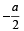

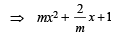 = 0 ⇒ m2 x2 + 2x + m = 0
= 0 ⇒ m2 x2 + 2x + m = 0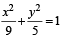
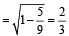
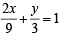
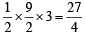
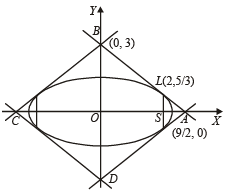
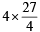 = 27 sq. units.
= 27 sq. units.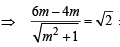
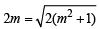
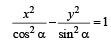
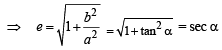
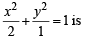
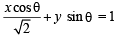
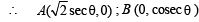
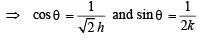
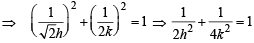
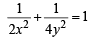
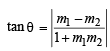
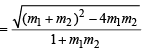
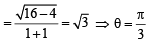
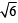 y = 2 or 4 x + 2
y = 2 or 4 x + 2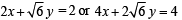
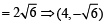
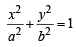
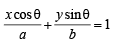
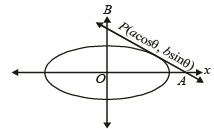
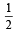 x a secθ × b cosecθ
x a secθ × b cosecθ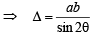
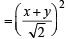
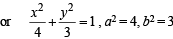
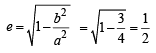
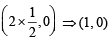
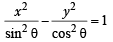
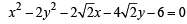
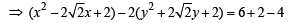
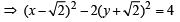
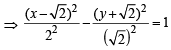
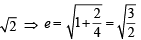
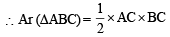 =
= 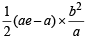
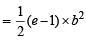 =
= 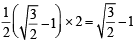
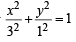
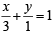
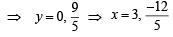
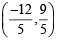
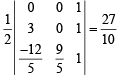
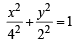
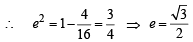

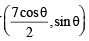
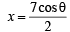 and y = sinθ
and y = sinθ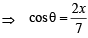 and sinθ= y
and sinθ= y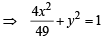 ...(1)
...(1)