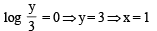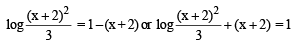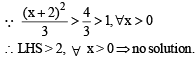Test: JEE Advanced (One or More Correct Option)- Differential Equations - JEE MCQ
9 Questions MCQ Test - Test: JEE Advanced (One or More Correct Option)- Differential Equations
The order of the differential equation whose general solution is given by
y = (C1 + C2) cos (x+C3) – C4ex+C5, where C1, C2, C3, C4, C5, are arbitrary constants, is
The differential equation representing the family of curves 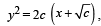 where c is a positive parameter, is of
where c is a positive parameter, is of
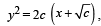 where c is a positive parameter, is of
where c is a positive parameter, is ofA curve y = f (x) passes through (1, 1) and at P(x, y), tangent cuts the x–axis and y–axis at A and B respectively such that BP : AP = 3 : 1, then
If y (x) satisfies the differential equation y ' – y tan x = 2x secx and y(0) = 0, then
A curve passes through the point 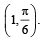 Let the slope of the curve at each point (x, y) be
Let the slope of the curve at each point (x, y) be 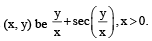
Then the equation of the curve is
Let y (x) be a solution of the differential equation (1 + ex) y ' + yex = 1 . If y(0) = 2, then which of the following statement is (are) true?
Consider the family of all circles whose centers lie on the straight line y = x. If this family of circle is represented by the differential equation Py '' + Qy' + 1=0 , where P, Q are functions of x, y and y' 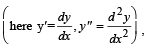 then which of the following statements is (are) true?
then which of the following statements is (are) true?
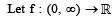 be a differentiable function such that
be a differentiable function such that 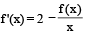 for all x ∈ (0, ∞) and f(1) ≠ 1. Then
for all x ∈ (0, ∞) and f(1) ≠ 1. Then
A solution curve of the differen tial equation 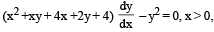 passes through thepoint (1, 3). Then the solution curve
passes through thepoint (1, 3). Then the solution curve


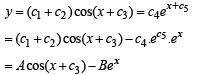
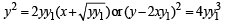

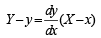
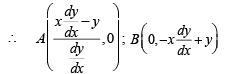

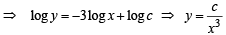
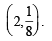
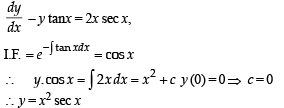
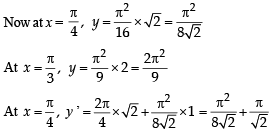
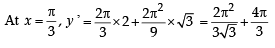
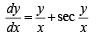
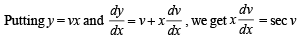
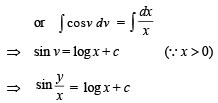

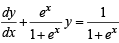
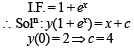

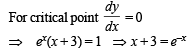
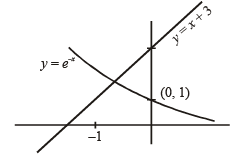
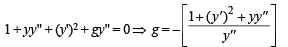
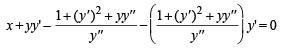
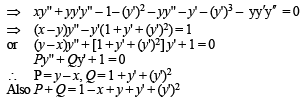
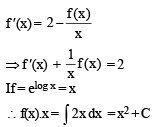

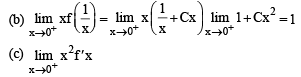
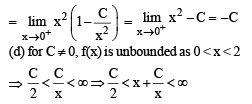
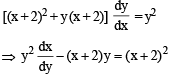
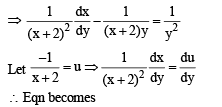
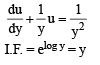
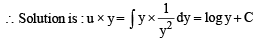
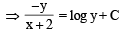
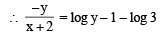
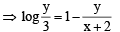 ..(1)
..(1)