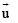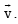Test: MCQs (One or More Correct Option): Vector Algebra and Three Dimensional Geometry | JEE Advanced - BMAT MCQ
20 Questions MCQ Test - Test: MCQs (One or More Correct Option): Vector Algebra and Three Dimensional Geometry | JEE Advanced
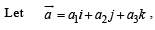
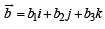 and
and 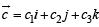 be three non-zero vectors such that
be three non-zero vectors such that 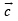 is a unit vector perpendicular to both the vectors
is a unit vector perpendicular to both the vectors 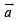 and
and 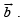 If the angle between
If the angle between 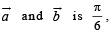 then
then
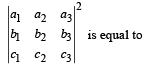
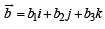 and
and 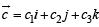 be three non-zero vectors such that
be three non-zero vectors such that 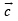 is a unit vector perpendicular to both the vectors
is a unit vector perpendicular to both the vectors 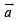 and
and 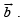 If the angle between
If the angle between 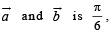 then
then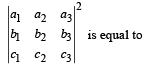
The number of vectors of unit length perpendicular to vectors 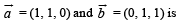
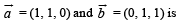
Let 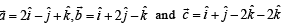 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 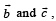 whose projection on
whose projection on 
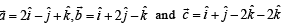 be three vectors. A vector in the plane of
be three vectors. A vector in the plane of 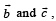 whose projection on
whose projection on 
The vector 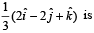
If 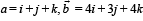 and
and 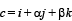 are linearly dependent vectors and
are linearly dependent vectors and 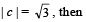
For three vectors u, v, w which of the following expression is not equal to any of the remaining three?
Which of the following expressions are meaningful?
Let a and b be two non-collinear unit vectors. If u = a – (a . b) b and v = a × b, then | v | is
Let 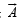 be vector parallel to line of intersection of planes P1 and P2. Plane P1 is parallel to the vectors
be vector parallel to line of intersection of planes P1 and P2. Plane P1 is parallel to the vectors 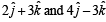 and that P2 is parallel to
and that P2 is parallel to 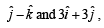 then the angle between vector
then the angle between vector 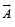 and a given vector
and a given vector 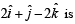
The vector (s) which is/are coplanar with vectors 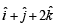 and
and 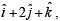 and perpendicular to the vector
and perpendicular to the vector 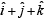 is/are
is/are
If the straight lines 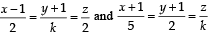 are coplanar, then the plane (s) containing these two lines is (are)
are coplanar, then the plane (s) containing these two lines is (are)
A line l passing through the origin is perpendicular to the lines
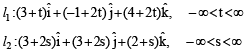
Then, the coordinate(s) of the point(s) on l2 at a distance of 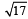 from the point of intersection of l and l1 is (are)
from the point of intersection of l and l1 is (are)
Two lines 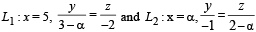 are coplanar. Then a can take value(s)
are coplanar. Then a can take value(s)
Let 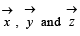 be three vectors each of magnitude
be three vectors each of magnitude 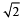 and the angle between each pair of them is
and the angle between each pair of them is 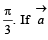 is a non-zero vector perpendicular to
is a non-zero vector perpendicular to 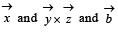 is a non-zero vector perpendicular to
is a non-zero vector perpendicular to 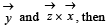
From a point P(λ, λ, λ), perpendicular PQ and PR are drawn respectively on the lines y = x, z = 1 and y = – x, z = – 1. If P is such that ∠QPR is a right angle, then the possible value(s) of ∠ is/(are)
In R3, consider the planes P1 : y = 0 and P2 : x + z = 1. Let P3 be the plane, different from P1 and P2, which passes through the intersection of P1 and P2. If the distance of the point (0, 1, 0) from P3 is 1 and the distance of a point (α, β, γ) from P3 is 2, then which of the following relations is (are) true?
In R3, let L be a straight line passing through the origin. Suppose that all the points on L are at a constant distance from the two planes P1 : x + 2y – z + 1 = 0 and P2 : 2x – y + z – 1 = 0. Let M be the locus of the feet of the perpendiculars drawn from the points on L to the plane P1. Which of the following points lie (s) on M?
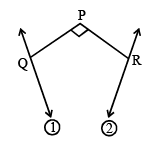
Let ΔPQR be a triangle. 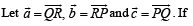
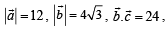 then which of the following is (are) true?
then which of the following is (are) true?
Consider a pyramid OPQRS located in the first octant (x > 0, y > 0, z > 0) with O as origin, and OP and OR along the x–axis and the y–axis, respectively. The base OPQR of the pyramid is a square with OP = 3. The point S is directly above the mid-point, T of diagonal OQ such that TS = 3. Then
Let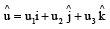 be a unit vector in R3 and
be a unit vector in R3 and 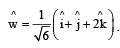 Given that there exists a vector
Given that there exists a vector 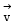 in
in 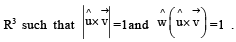 Which of the following statement(s) is (are) correct?
Which of the following statement(s) is (are) correct?


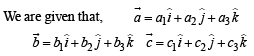
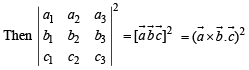
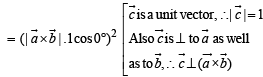
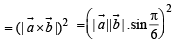
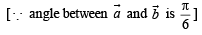
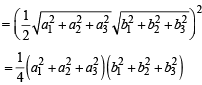
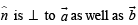 then
then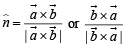
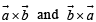 represent two vectors in opp. directions.
represent two vectors in opp. directions. 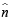

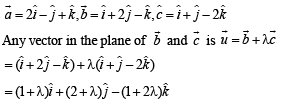
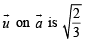
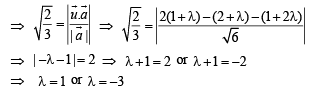
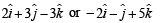
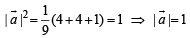
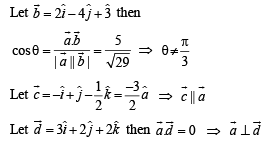
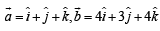 and
and 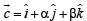 are linearly dependent,
are linearly dependent,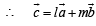 for some scalars l and m not all zeros.
for some scalars l and m not all zeros.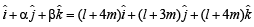
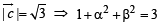
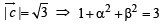
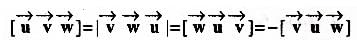
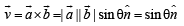
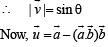
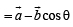
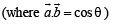

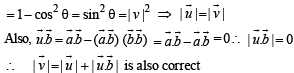
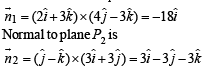
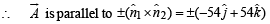
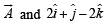 is given by
is given by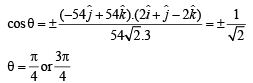
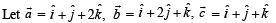
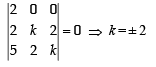
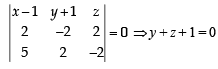
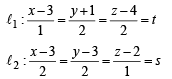
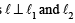
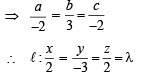

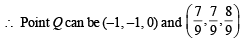
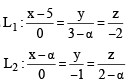
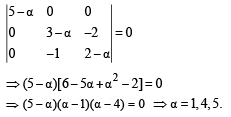
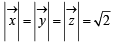
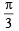
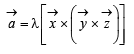
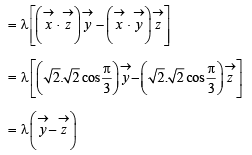
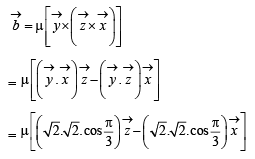
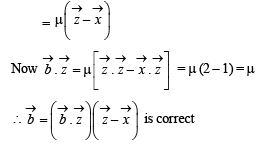
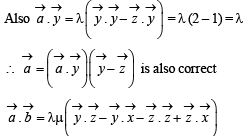
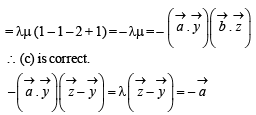
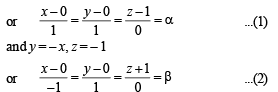
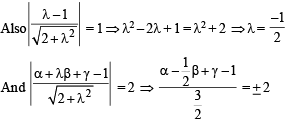
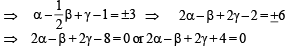
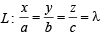
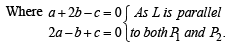
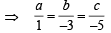
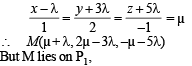
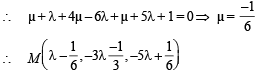
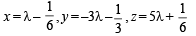
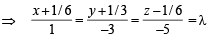
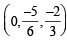 and
and 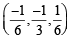 satisfy the above eqn.
satisfy the above eqn.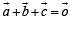
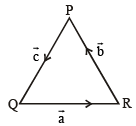
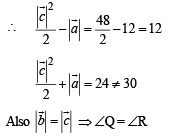
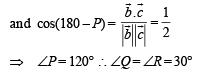
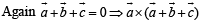
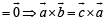
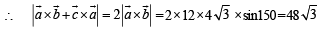
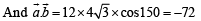
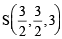
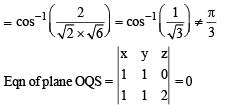
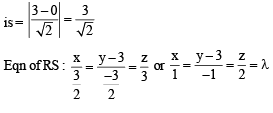
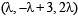
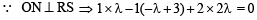
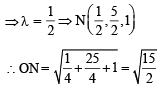
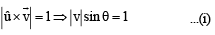
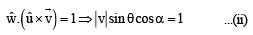
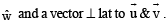
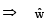 is perpendicular to the plane containing
is perpendicular to the plane containing 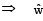 is perpendicular to
is perpendicular to