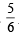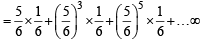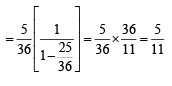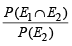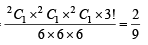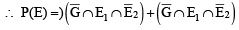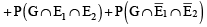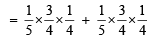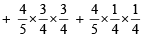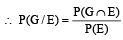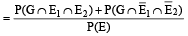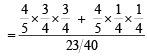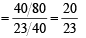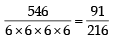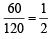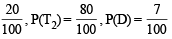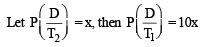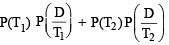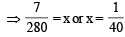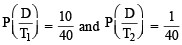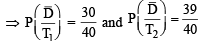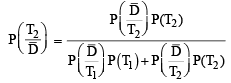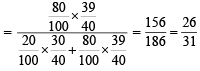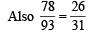JEE Advanced (Single Correct MCQs): Probability - JEE MCQ
27 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Probability
Two fair dice are tossed. Let x be the event that the first die shows an even number and y be the event that the second die shows an odd number. The two events x and y are :
Two events A an d B ha ve pr obabilities 0.25 an d 0.50 respectively. The probability that both A and B occur simultaneously is 0.14. Then the probability that neither A nor B occurs is (1980)
The probability that an event A happens in one trial of an experiment is 0.4. Three independent trials of the experiment are performed. The probability that the event A happens at least once is (1980)
If A and B are two events such that P(A) > 0, and P(B) ≠ 1 ,then 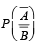 is equal to (Here
is equal to (Here 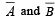 are complements of A and B respectively). (1982 - 2 Marks)
are complements of A and B respectively). (1982 - 2 Marks)
Fifteen coupons are numbered 1, 2 ..... 15,respectively. Seven coupons are selected at random one at a time with replacement. The probability that the largest number appearing on a selected coupon is 9, is (1983 - 1 Mark)
Three identical dice are rolled. The probability that the same number will appear on each of them is (1984 - 2 Marks)
A box con t ain s 24 iden tical balls of wh ich 12 ar e wh ite and 12 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the 4th time on the 7th draw is (1984 - 2 Marks)
One hundred identical coins, each with probability, p, of showing up heads are tossed once. If 0 < p < 1 and the probabilitity of heads showing on 50 coins is equal to that of heads showing on 51 coins, then the value of p is (1988 - 2 Marks)
In dia plays two matches each with West In dies and Australia. In any match the probabilities of India getting, points 0, 1 and 2 are 0.45, 0.05 and 0.50 respectively.Assuming that the outcomes are independent, the probability of India getting at least 7 points is (1992 - 2 Marks)
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled four times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5, is then: (1993 - 1 Mark)
Let A , B , C be three mutually independent events.Consider the two statements S1 and S2 S1 : A and B ∪ C are independent S2 : A an d B ∩ C are independent Then,(1994)
The probability of India winning a test match against west Indies is 1/2. Assuming independence from match to match the probability that in a 5 match series India’s second win occurs at third test is (1995S)
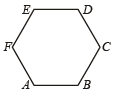
Three of the six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral, equals (1995S)
For the three events A, B, and C, P (exactly one of the events A or B occurs) = P (exactly one of the two events B or C occurs) = P(exactly one of the events C or A occurs) = p and P (all the three events occur simultaneously) = p2, where 0 < p < 1/2. Then the probability of at least one of the three events A, B and C occurring is (1996 - 2 Marks)
If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form 7m + 7n is divisible by 5 equals (1999 - 2 Marks)
Two numbers are selected randomly from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is (2003S)
If three distinct numbers are ch osen randomly from the first 100 natural numbers, then the probability that all three of them are divisible by both 2 and 3 is (2004S)
A six faced fair dice is thrown until 1 comes, then the probability that 1 comes in even no. of trials is (2005S)
One Indian and four American men and their wives are to be seated randomly around a circular table. Then the conditional probability that the Indian man is seated adjacent to his wife given that each American man is seated adjacent to his wife is (2007 -3 marks)
Let Ec denote the complement of an event E. Let E, F, G be pairwise independent events with P(G) > 0 and P(E∩F∩G) = 0. Then P(Ec∩ Fc| G) equals (2007 -3 marks)
An experiment has 10 equally likely outcomes. Let A and B be non-empty events of the experiment. If A consists of 4 outcomes, the number of outcomes that B must have so that A and B are independent, is (2008)
Let ω be a complex cube root of unity with ω ≠ 1. A fair die is thrown three times. If r1, r2 and r3 are the numbers obtained on the die, then the probability that ωr1 + ωr2 + ωr3 = 0 is (2010)
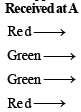
A signal which can be green or red with probability 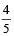 and
and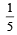 respectively, is received by station A and then transmittedto station B. The probability of each station receiving the signal correctly is
respectively, is received by station A and then transmittedto station B. The probability of each station receiving the signal correctly is 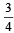 . If the signal received at station B is green, then the probability that the original signal was green is
. If the signal received at station B is green, then the probability that the original signal was green is
(2010)
Four fair dice D1, D2, D3 and D4 ; each having six faces numbered 1, 2, 3, 4, 5 and 6 are rolled simultaneously.
The probability that D4 shows a number appearing on one of D1, D2 and D3 is (2012)
Three boys and two girls stand in a queue. The probability, that the number of boys ahead of every girl is at least one more than the number of girls ahead of her, is (JEE Adv. 2014)
A computer producing factory has only two plants T1 and T2. Plant T1 produces 20% and plant T2 produces 80% of the total computers produced. 7% of computers produced in the factory turn out to be defective. It is known that P (computer turns out to be defective given that it is produced in plant T1) = 10P (computer turns out to be defective given that it is produced in plant T2), where P(E) denotes the probability of an event E. A computer produced in the factory is randomly selected and it does not turn out to be defective. Then the probability that it is produced in plant T2 is (JEE Adv. 2016)



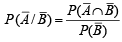
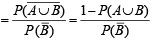
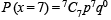 [Binomial distribution]
[Binomial distribution]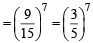
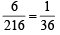

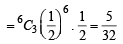
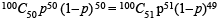
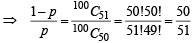 ⇒ 51 – 51 p = 50 p
⇒ 51 – 51 p = 50 p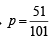
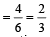
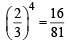


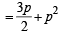 [using (4) and (5)]
[using (4) and (5)] 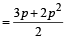
 (25 options each) [7 + 3 = 10]
(25 options each) [7 + 3 = 10] (25 options each) [9 + 1= 10]
(25 options each) [9 + 1= 10]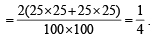
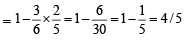
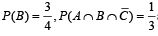 and
and 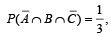 then P (B∩C) is (2003S)
then P (B∩C) is (2003S)
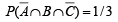
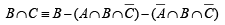
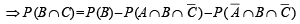
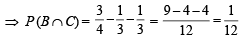
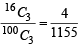
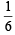 and prob. of not getting 1 is
and prob. of not getting 1 is