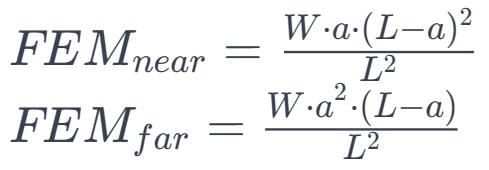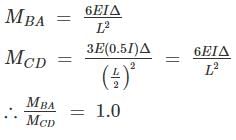Test: Theory of Structures - SSC JE MCQ
20 Questions MCQ Test - Test: Theory of Structures
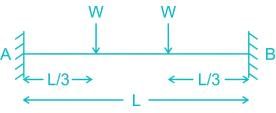
What are the bending moments at ends A and B of uniform fixed beam AB as shown in figure when two concentrated loads acts at 1/3 spans?

When on end of a fixed beam deflects by δ, then the bending moment at deflected end is
If ∑H and ∑V are the algebraic sums of the forces resolved horizontally and vertically respectively, and ∑M is the algebraic sum of the moments of forces about any point, for the equilibrium of the body acted upon.
A two hinge arch of span 40 m carries a point load of 62.8 KN at its crown. The Horizontal thrust in the arch is (in KN)
What is the degree of static indeterminacy of the structure shown in figure below?
If a system has more equations of equilibrium than no. of forces, then the system is:-
Which of the following material is not used in making trusses?
The Muller-Breslau principle in structure analysis is used for
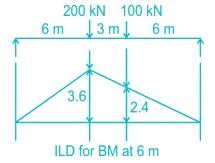
The influence line diagram for bending moment at 6 m is shown. The value of the maximum bending moment is:
The degree of static indeterminacy of the pin - jointed plane truss as shown in figure is
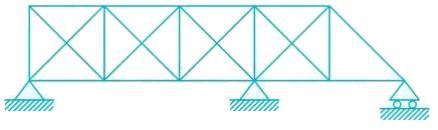
Due to rising temperature in a three hinged arch, induced stress is:
Which of the following equals the number of unknowns to be determined, in stiffness method of structural analysis?
The degree of kinematic indeterminacy of the given beam considering axial rigidity is
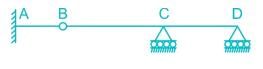
Consider the following statements:
The principle of superposition is not applicable when
1. The material does not obey Hooke’s law
2. The effect of temperature changes are taken into consideration
3. The structure is being analysed for the effect of support settlement
Which of these statement (s) is/are correct?
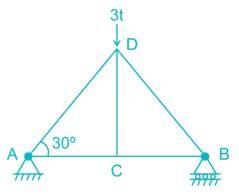
Force in the member BC of the truss shown in the given figure is
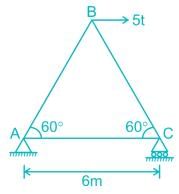
Clapeyron’s theorem is associated with the analysis of
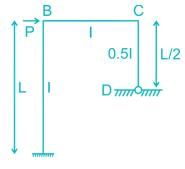
The given figure shows a portal frame with one end fixed and other hinged. The ratio of the fixed end moments 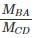 due to side sway will be
due to side sway will be