Important Questions: The Triangle and Its Properties - JSS 2 MCQ
10 Questions MCQ Test - Important Questions: The Triangle and Its Properties
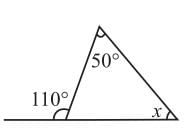
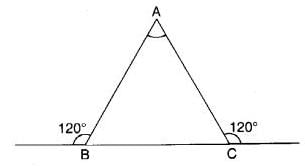
Find the measure of the angle x in the given figure.
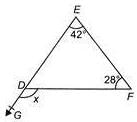

In the figure (not drawn to scale), ABC is an equilateral triangle and ABD is an isosceles triangle with DA = DB, find x.
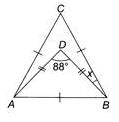

In the following figure, the measure of ∠A is

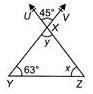
Find the measure of the angle ∠x in the given figure.
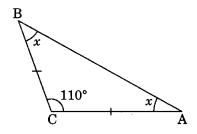
In ΔABC, AC = BC and ∠C = 110°. Find ∠A and ∠B.
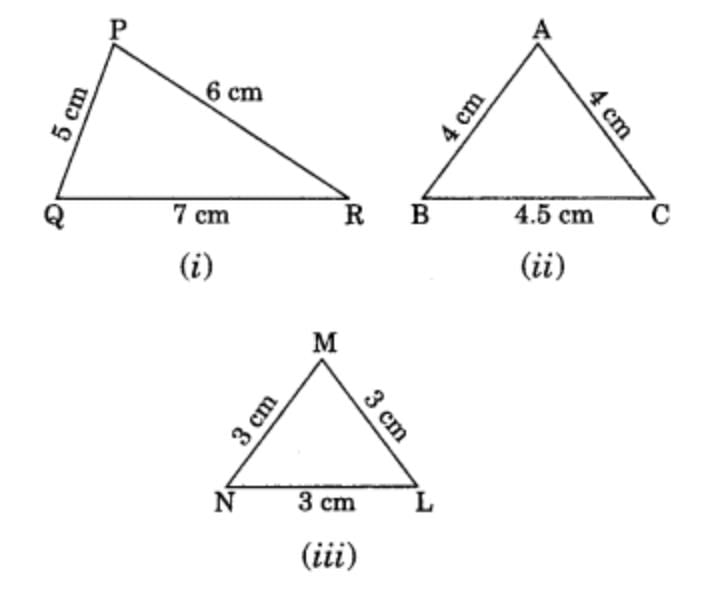
Classify the following triangle on basis of their sides
If one of the interior opposite angles of an exterior angle is 45∘ and the exterior angle is 130∘, what is the measure of the second interior opposite angle?
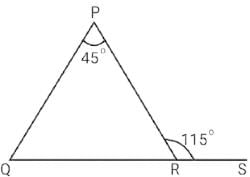
In the given figure, the side QR of a △PQR has been produced to the point S. If ∠PRS = 115o and ∠P = 45o , then ∠Q is equal to,
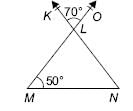
Find the measure of ∠LNM in the given figure.