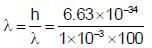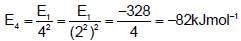Atomic Structure - Class 12 MCQ
30 Questions MCQ Test - Atomic Structure
Two electrons A and B in an atom have the following set of quantum numbers :
A : 3, 2, -2, +1/2, B : 3, 0, 0, +1/2,
Which statement is correct for A and B ?
A : 3, 2, -2, +1/2, B : 3, 0, 0, +1/2,
Which statement is correct for A and B ?
Which have the same number of s-electrons as the d-electrons in Fe2+ ?
Which set has the same number of unpiared electrons in their ground state?
Which statement does not form part of Bohr’s model of the hydrogen atom?
The statement are valid for :
(I) in filling a group of orbitals of equal energy it is energetically preferable to assign electron to empty orbitals rather than pair them into a particular orbital.
(II) when two electrons are placed in two different orbitals, energy is lower if the spins are parallel.
If E1,E2 and E3 represent respectively the kinetic energies of an electron, an alpha particle and a proton each having same de Broglie wavelength then :
The angular speed of the electron in the nth orbit of Bohr hydrogen atom is :
When atoms are bombarded with α-particles, only a few in million of the α-particles suffer deflections, while others pass through undeflected.
What is the correct orbital designation for the electron with the quantum number, n = 4, m = -2, s = 1/2?
Photoelectric emission is observed from a surfcae for frequency v1 and v2 of the incident radiation (v1 > v2). If the maximum kinetic ebergies of the photoelectrons in the two cases are in the ratio 1:k, then the threshold frequency v0 is given by :
The radii of two of the first four Bohr’s orbits of the hydrogen atom are in the ratio 1 : 4. The energy difference between them may be:
When photons of energy 4.25eV strike the surface of a metal A, the ejected photoelectrons have maximum kinetic energy, TA (expressed in eV) and de broglie wavelength,λA, The maximum kinetic energy of photoelectrons liberated from another metal B by photons of energy 4.70V is TB = TA - 1.50 eV. If the de Broglie wavelength of these photoelectrons is =,λB = 2λA then which is not correct?
The de Broglie wavelength of a particle with mass 1g and velocity 100m/s is:
The uncertainty in the momentum of an electron is 10-5 kg m s-1. The uncertainty in its position will be:
The energy of second Bohr’s orbit in H-atom is -328 kJ mol-1, hence the energy of fourth Bohr orbit would be :



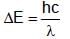
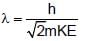
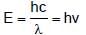
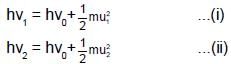
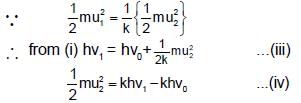

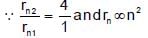

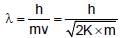
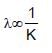 (K is kinetic energy)
(K is kinetic energy)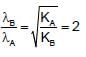
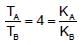
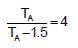
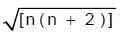 where n is number of unpaired electrons.
where n is number of unpaired electrons.