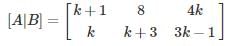Test: Engineering Mathematics- 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Engineering Mathematics- 1
Find the value of k for which the following system of equations will be consistent.
2x – 5y = 10 and 6x – 15y = k
The system of equation, 5x + 2y + z = 3,7x + 10y + 2z = 7,2x + 8y + z = 4 has
Matrix for which LU decomposition is not possible?
If the coefficient matrix is Cn x n and its corresponding rank is c also the augmented matrix is An x (n+1) and its corresponding rank is a, then how many statements given below are incorrect?
I. If c ≠ a, the equations are inconsistent with an infinite number of solutions.
II. If c = a < n, the equations are inconsistent
III. If c = a =n, equation may be inconsistent.
Find the value of x and y for the below given simultaneous equations that has no solutions?
a + b + c = 18
2a + 4b + 6c = 12
2a + xc + 4b = y
In the LU decomposition of the matrix, 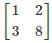 , if the diagonal elements of U are both 1, then the trace of L is:
, if the diagonal elements of U are both 1, then the trace of L is:
Consider the following system of equations in three real variables x, y, z.
2x – 3y + 7z = 5
3x + y – 3z = 13
2x + 19y – 47z = 32
The system of the equation has
Among the given two sets which is/are consistent:
S1 = {3x + ay + 4z = 0,bx + 2y + z = 0,5x + 7z + 9z = 0
S2 = {2x + 6y= −11, 6x + 20y − 6z = −3, 6y − 18z = −1}
The number of values of k for which the system of equations (k + 1) x + 8y = 4k, kx + (k + 3)y = 3k – 1 has infinitely many solutions, is
The simultaneous equations
2x + ay + z = 20
x + 3y + 4z = b
x + 2y + 3z = c
has unique solution then what is the value of a, b and c respectively?


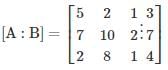
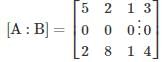

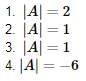
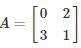 in this leading sub matrix A = [0]
in this leading sub matrix A = [0]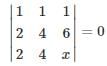

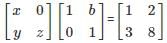
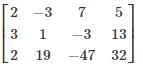
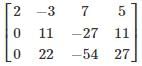



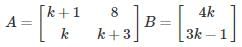 The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2
The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2