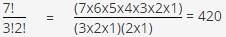Test: Problem Solving- 3 - SSC CGL MCQ
10 Questions MCQ Test - Test: Problem Solving- 3
A code is to be made by arranging 7 letters. Three of the letters used will be the letter A, two of the letters used will be the letter B, one of the letters used will be the letter C, and one of the letters used will be the letter D. If there is only one way to present each letter, how many different codes are possible?
If x is an integer and 2.134 x 10x is less than 210,000, what is the greatest possible value for x?
John spent 40 percent of his earnings last month on rent and 30 percent less than what he spent on rent to purchase a new dishwasher. What percent of last month's earnings did John have left over?
If negative integers k and p are NOT both even, which of the following must be odd?
Peter read P books last year, and Nikki read N books last year. If Peter read 35 more books than Nikki last year, which of the following reflects the relationship?
If 2 is the remainder when m is divided by 5, what is the remainder when 3m is divided by 5?
To fill and art exhibit, the students in an art course are assigned to create one epiece of artwork each in the following distribution: 1⁄3 are sculptures, 1⁄8 are oil paintings, 1⁄2 are watercolors and the remaining 10 pieces are mosaics. How many students are in the art class?
A computer company's featured laptop cost $800 last year. This year, the laptop sold for 15% less than it did last year. Next year, after updates are made to the model, there will be a 25% price increase over this year's price. What will be the price next year?
If two distinct integers a and b are picked from {1, 2, 3, 4, .... 100} and multiplied, what is the probability that the resulting number has EXACTLY 3 factors ?