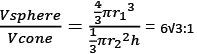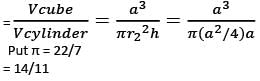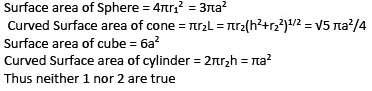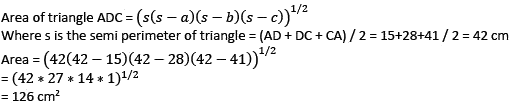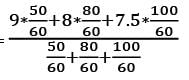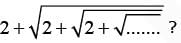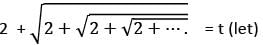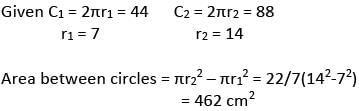CDS I - Mathematics Previous Year Question Paper 2019 - CDS MCQ
30 Questions MCQ Test - CDS I - Mathematics Previous Year Question Paper 2019
Direction: Consider the following for the next three (03) items :
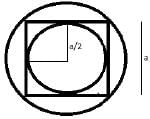
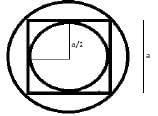
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
Q. What is the ratio of the volume of the sphere to that of cone?
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
Direction: Consider the following for the next three (03) items :
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
Q. What is the ratio of the volume of the cube to that of the cylinder ?
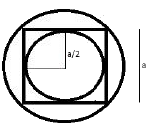
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
Q. What is the ratio of the volume of the cube to that of the cylinder ?
Direction: Consider the following for the next three (03) items :
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
1) The surface area of the sphere is √5
Times the curved surface area of the cone.
2) The surface area of the cube is equal to the curved surface area of the cylinder.
Q. Which of the above statements is/are correct?
A cube is inscribed in a sphere. A right circular cylinder is within the cube touching all the vertical faces. A right circular once is inside the cylinder. Their heights are same and the diameter of the cone is equal to that of the cylinder.
1) The surface area of the sphere is √5
Times the curved surface area of the cone.
2) The surface area of the cube is equal to the curved surface area of the cylinder.
Q. Which of the above statements is/are correct?
Direction: Consider the following for the next three (03) items:
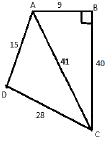
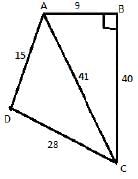
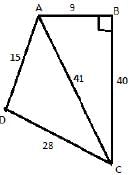
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right – angel
Q. What is the area of triangle ADC?
Direction: Consider the following for the next three (03) items:
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right – angel
Q. What is the area of quadrilateral ABCD?
Direction: Consider the following for the next three (03) items:
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right – angel
Q. What is the difference between perimeter of triangle ABC and perimeter of triangle ADC?
Direction: Consider the following for the next two (02) items:
An equilateral triangle ABC is inscribed in a circle of radius 20√3
Q. What is the length of the side of the triangle?
Direction: Consider the following for the next two (02) items:
An equilateral triangle ABC is inscribed in a circle of radius 20√3
Q. The centroid of the triangle ABC is at a distance d from the vertex A. What is d equal to?
Direction: Consider the following for the next two (02) items:
The sum of length, breadth and height of a cuboid is 22 cm and the length of its diagonal is 14 cm.
Q. What is the surface area of the cuboid?
Direction: Consider the following for the next two (02) items:
The sum of length, breadth and height of a cuboid is 22 cm and the length of its diagonal is 14 cm.
Q. If S is sum of the cubes of the dimensions of the cuboid and V is its volume, then what is (S-3V) equal to?
A race has three parts. The speed and time required to complete the individual parts for a runner is displayed on the following chart:
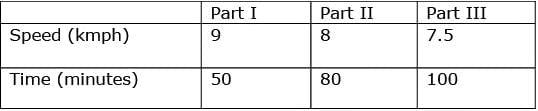
Q. What is the average speed of this runner?
If  then which one of the following statements is correct?
then which one of the following statements is correct?
The number 3521 is divided by 8. What is the remainder?
A prime number contains the digit X at unit’s place. How many such digits of X are possible?
If an article is sold at a gain of 6% instead of a loss of 6% the seller gets Rs. 6 more. What is the cost price of the article?
A field can be reaped by 12 men or 18 women in 14 days. In how many days can 8 men and 16 women reap it?
If 3x = 4y = 12z, then z is equal to
If (4a +7b) (4c-7d) = (4a -7b) (4c +7d, then which one of the following is correct?
GiGiven that the polynomial (x2 + ax + b) leaves that same remainder when by (x – 1) or (x + 1) What are the values of a and b respectively?
Tushar takes 6 hours to complete a piece of work, while Amar completes the same work in 10 hours. If both of them work together, then what is the time required to complete the work?
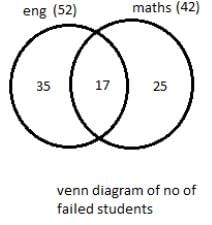
In an examination, 52% candidates failed in English and 42% failed in Mathematics. If 17% failed in both the subjects, then what percent passed in both the subjects?
A man who recently died left a sum of Rs. 3,90,000 to be divided among his wife, five sons and four daughters. He directed that each son should receive 3 times as much as each daughter receives and that each daughter receives and that each daughter should receive twice as much as their mother receives. What was the wife’s share?
What is the least number of complete years in which a sum of money put out at 40% annual compound interest will be more than trebled?
A person divided a sum of Rs. 17,200 into three parts and invested at 5%. 6% and 9^ per annum simple interest. At the end of two years, he got the same interest on each part of money. What is the money invested at 9%?
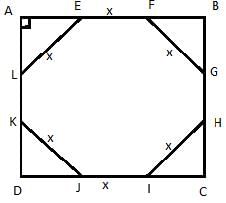
The corners of a square of side ‘a’ are cut away so as to form a regular octagon. What is the side of the octagon?
Three consecutive integers form the lengths of a right-angled triangle. How many sets of such three consecutive integers is/are possible?
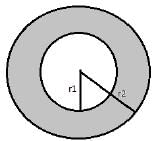
Two circles are drawn with the same centre. The circumference of the smaller circle is 44 cm and that of the bigger circle is double the smaller one. What is the area between these two circles?
A rectangular red carpet of size 6 ft × 12 ft has a dark red border 6 inches wide. What is the area of the dark red border?
The perimeter of a right-angled triangle is k times the shortest side. If the ratio of the other side to hypotenuse is 4 : 6, then what is the value of k?