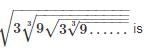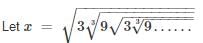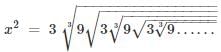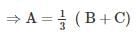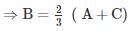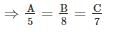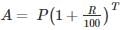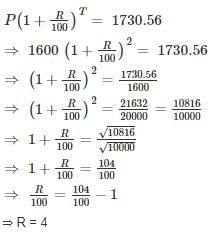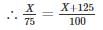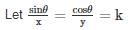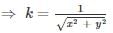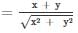Practice Test: Quantitative Aptitude - 3 - SSC CGL MCQ
25 Questions MCQ Test - Practice Test: Quantitative Aptitude - 3
Which of the following numbers is the smallest?


The number of students in a class is increased by 20% and the number now becomes 66. Initially the number was
The price of a jewel varies as the square of its weight. Two jewels A and B whose weights are in the ratio of 3 and 5 are combined and made a new jewel C. What is the ratio of price of C to the combined price of A and B?
4 litres of a 40% solution of spirit in water is mixed with 6 litres of a 50% solution of spirit in water. What is the strength of spirit in the resulting mixture?
If LCM of two numbers is thrice the larger number and difference between the smaller number and the HCF is 14. Then, find out the smaller number of the two numbers.
The ratio of ages of A and B is 11 : 13 respectively. After 7 years the ratio of their ages will be 20 : 23. What is the difference between their ages?
By selling cloth at Rs. 9 per metre, a shopkeeper loses 10%. Find the rate at which it should be sold so as to earn profit of 15%
Rs. 3,000 is divided among A, B and C, so that A receives 1/3 as much as B and C together receive and B receives 2/3 as much as A and C together receive. Then share of C is
At some rate per annum the amount with compound interest on Rs. 1600 for 2 years is Rs. 1730.56. The rate of interest per annum is:
I walk a certain distance and ride back taking a total time of 37 minutes. I could walk both ways in 55 minutes. How long would it take me to ride both ways?
Two trains start at the same time from two point P and Q and proceed towards each other at the speed of 75 km/hr and 100 km/hr respectively. When they meet, it is found that first train has travelled 125 km less than the second train. Find the distance between point P and Q.
Aman and Akbar together can do a work in 18 days. Both of them began to work. After 4 days Akbar fell ill, Aman completed the remaining work in 42 days. In how many days can Aman complete the whole work if he did it alone?
The sides of a right-angled triangle forming right angle are in the ratio 5 : 12. If the area of the triangle is 270 cm2, then the length of the hypotenuse is
Compute the ratio of the volumes of two cylinders if the ratio of radii of the bases is 9 : 4 and the ratio of their heights is 3 : 7
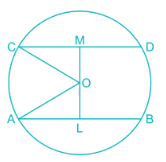
AB and CD are two parallel chords on the opposite sides of the centre of the circle. If AB = 18 cm, CD = 24 cm and the radius of the circle is 15 cm, the distance between the chords is
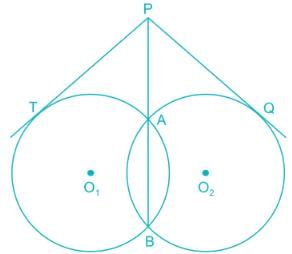
Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
If XYZ is an equilateral triangle and S is a point on YZ such that XS ⊥ YZ, then
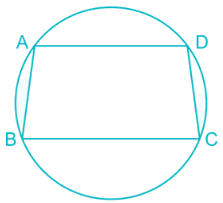
ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC = 72°, then the measure of the ∠BCD is
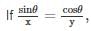 sinθx=cosθy,then sinθ + cos θ is equal to
sinθx=cosθy,then sinθ + cos θ is equal to
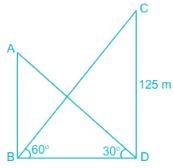
The angle of elevation of the top a tower form the base of a building is 60° and the angle of elevation of the top of the building from the base of the tower is 30°. If the height of tower is 125 m, find the height of the building.
The value of 2cos220° + 3cos270° + sin270° is
5 years ago the average age of a family of 3 members was 19 years. A baby having been born, the average age of the family remains the same today. The age of the baby after 8 years would be
The sum of all odd numbers between 11 and 61 is


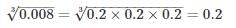
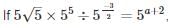 then a is equal to
then a is equal to