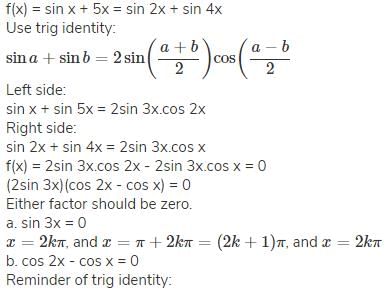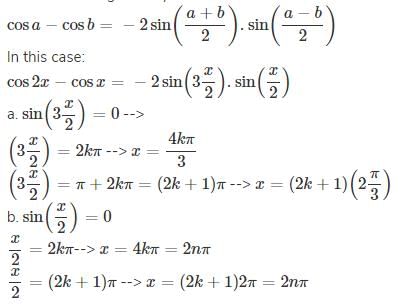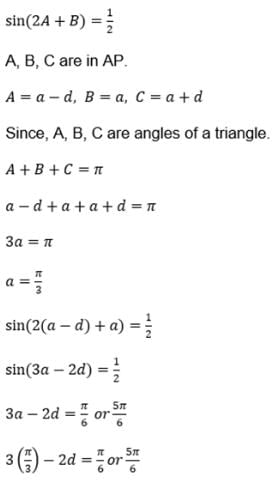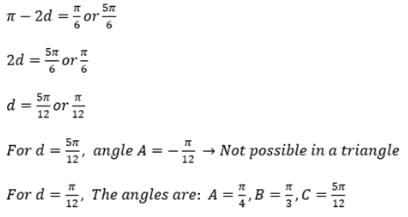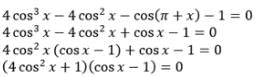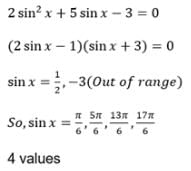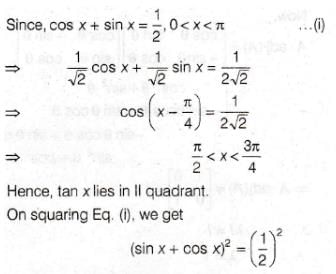JEE Advanced Level Test: Trigonometric Equations- 1 - Airforce X Y / Indian Navy SSR MCQ
26 Questions MCQ Test - JEE Advanced Level Test: Trigonometric Equations- 1
The general solution of the equation, 2cos2x = 3.2cos2x – 4 is
The solution set of the equation 4sinθ . cosθ – 2 cosθ – 2√3 sinθ + √3 = 0 in the interval (0, 2π) is
Total number of solutions of sin x . tan 4x = cos x belonging to (0, π) are
All solutions of the equation, 2 sin θ + tan θ = 0 are obtained by taking all integral values of m and n in
The most general solution of tan θ = – 1 and cos θ = 1/√2 is
If 2 cos2 (π + x) + 3 sin (π + x) vanishes then the values of x lying in the interval from 0 to 2π are
If x ∈ , the number of solutions of the equation, sin 7x + sin 4x + sin x = 0 is
The general solution of sin x + sin 5x = sin 2x + sin 4x is
A triangle ABC is such that sin(2A + B) = 1/2. If A, B, C are in A.P. then the angle A, B, C are respectively
If sin θ + 7 cos θ = 5, then tan (θ/2) is a root of the equation
sin 3θ = 4 sin θ . sin 2θ . sin 4q in 0 < θ < π has
General solution of the equation, cot 3 θ – cot θ = 0 is
The set of values of x for which = 1 is
The principal solution set of the equation, 2 cos x = is
The number of all possible triplets (a1, a2, a3) such that : a1 + a2 cos 2x + a3 sin2x = 0 for all x is
The value 'a' for which the equation 4cosec2 (π(a + x)) + a2 – 4a = 0 has a real solution is
The solution of |cos x| = cosx – 2sinx is
The number of solutions of sin θ + 2sin 2θ + 3sin 3θ + 4sin 4θ = 10 in (0, π) is
The arithmetic mean of the roots of the equation 4cos3x – 4cos2x – cos(π + x) – 1 = 0 in the interval [0, 315] is equal to
Find the no. of roots of the equation tan x + sec x = 2 cos x in the interval [0, 2π]-
General solution of tan 5θ = cot 2θ is-
The number of values of x in the interval [0, 3π]satisfying the equation 2 sin2 x + 5 sin x – 3 = 0 is –
If 0 < x < π, and cos x + sin x = 1/2, then tan x is –