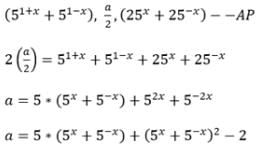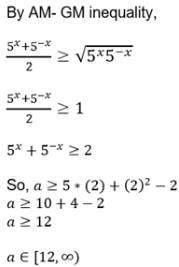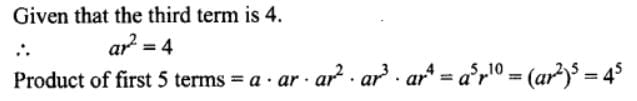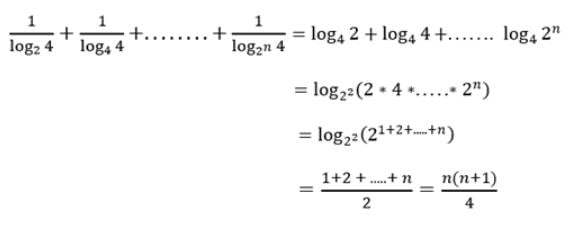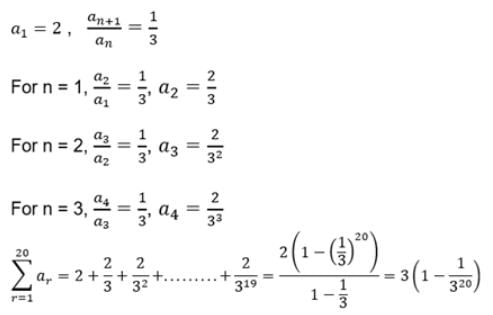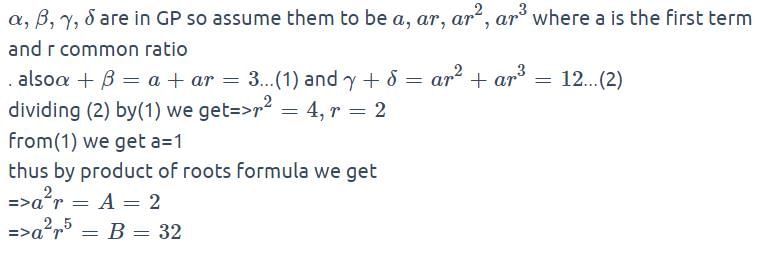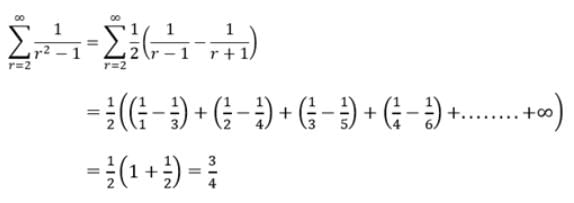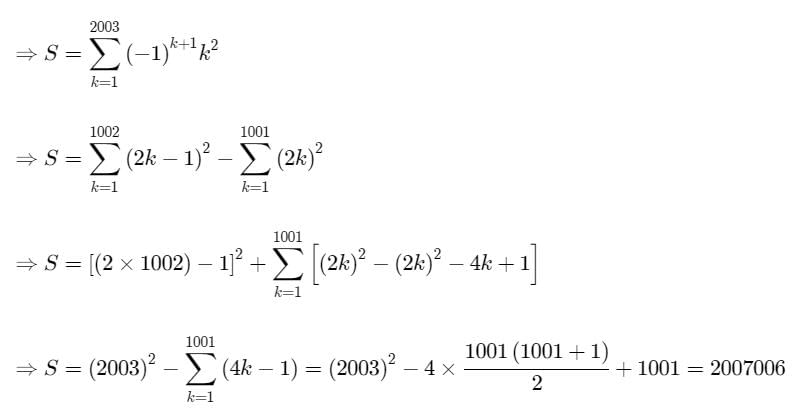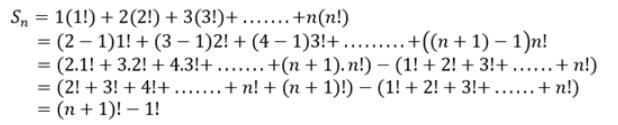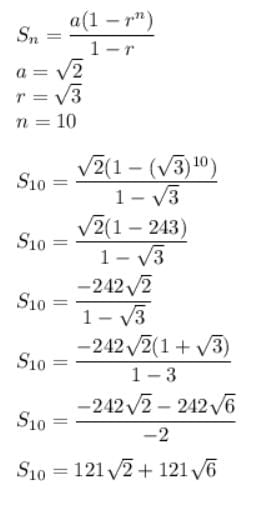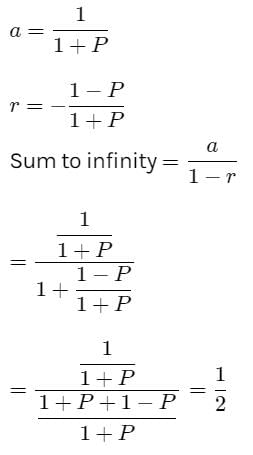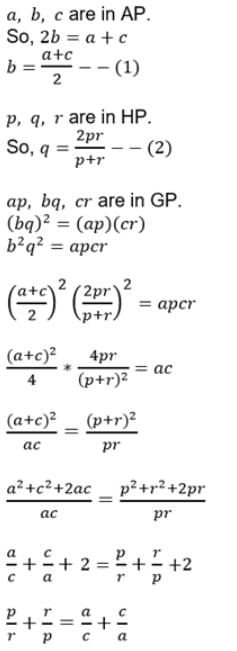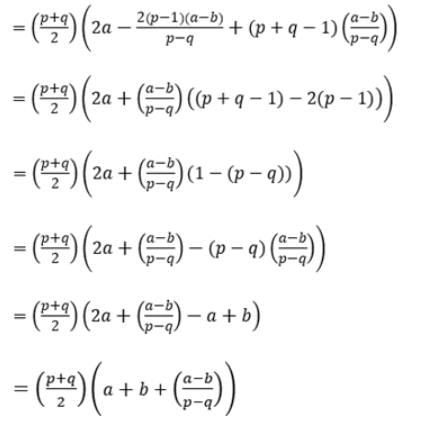JEE Advanced Level Test: Sequences And Series- 1 - JEE MCQ
22 Questions MCQ Test - JEE Advanced Level Test: Sequences And Series- 1
The first term of an A.P. of consecutive integer is p2 + 1. The sum of (2p + 1) terms of this series can be expressed as
If a1, a2, a3,........ are in A.P. such that a1 + a5 + a10 + a15 + a20 + a24 = 225, then a1 + a2 + a3 + ......+ a23 + a24 is equal to
If x ∈ R, the numbers 51+x + 51-x, a/2, 25x + 25-x form an A.P. then `a' must lie in the interval;
The third term of a G.P. is 4. The product of the first five terms is
If S is the sum of infinity of a G.P. whose first term is `a', then the sum of the first n terms is
The sum of the series +
+
+ ....... +
is
For a sequence {an}, a1 = 2 and . Then
is
a, b be the roots of the equation x2 – 3x + a = 0 and g, d the roots of x2 – 12x + b = 0 and numbers a, b, g, d (in this order) form an increasing G.P., then
If 3 + 1/4 (3 + d) + 1/42 (3 + 2d) + .... + upto ∞ = 8, then the value of d is
In a G.P. of positive terms, any term is equal to the sum of the next two terms. The common ratio of the G.P. is
If + ...... up to ∞ =
, then
+ ..... =
Sum of the series S = 12 – 22 + 32 – 42 + ..... – 20022 + 20032 is
If x =, y =
, z =
where a, b, c are in AP and |a| < 1, |b| < 1, |c| < 1, then x, y, z are in
The sum to n term of the series 1(1!) + 2(2!) + 3(3!) + ....
The sum to 10 terms of the series is
If p is positive, then the sum to infinity of the series, is
The positive integer n for which 2 × 22 + 3 × 23 + 4 × 24 + ..... + n × 2n = 2n + 10 is
If x > 0, and log2 x + log2 + log2
+ log2
+ log2
+ ....= 4, then x equals
If a, b, c are in A.P. p, q, r are in H.P. and ap, bq, cr are in G.P., then is equal to
12 + 22 + ......+ n2 = 1015, then value of n is
If a and b are pth and qth terms of an AP, then the sum of its (p + q) terms is