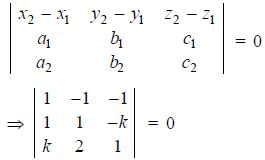JEE Advanced Level Test: Three Dimensional 3D Geometry- 1 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Three Dimensional 3D Geometry- 1
A line makes angles α,β,γ with the coordinates axes. If α+β = 90°, then (gamma) equal to
The coordinates of the point A, B, C, D are (4, α, 2), (5, –3, 2), (β, 1, 1) & (3, 3, – 1). Line AB would be perpendicular to line CD when
The locus represented by xy + yz = 0 is
The equation of plane which passes through (2, –3, 1) & is normal to the line joining the points (3, 4, –1) & (2, – 1, 5) is given by
If the sum of the squares of the distances of a point from the three coordinate axes be 36, then its distance from the origin is
The locus of a point P which moves such that PA2 – PB2 = 2k2 where A and B are (3, 4, 5) and (–1, 3, –7) respectively is
The equation of the plane passing through the point (1, – 3, –2) and perpendicular to planes x + 2y + 2z = 5 and 3x + 3y + 2z = 8, is
A variable plane passes through a fixed point (1, 2, 3). The locus of the foot of the perpendicular drawn from origin to this plane is
The reflection of the point (2, –1, 3) in the plane 3x – 2y – z = 9 is
The distance of the point (–1, –5, –10) from the point of intersection of the line, 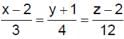 and the plane, x – y + z = 5, is
and the plane, x – y + z = 5, is
The distance of the point (1, –2, 3) from the plane x – y + z = 5 measured parallel to the line, 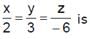
The straight l ines and
and 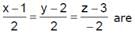
If plane cuts off intercepts OA = a, OB = b, OC = c from the coordinate axes, then the area of the triangle ABC equal to
A point moves so that the sum of the squares of its distances from the six faces of a cube given by x = ± 1, y = ± 1, z = ± 1 is 10 units. The locus of the point is
A variable plane passes through a fixed point (a, b, c) and meets the coordinate axes in A, B, C. Locus of the point common to the planes through A, B, C and parallel to coordinate plane, is
Two systems of rectangular axes have same origin. If a plane cuts them at distances a, b, c and a1, b1, c1 from the origin, then
The angle between the plane 2x – y + z = 6 and a plane perpendicular to the planes x + y + 2z = 7 and x – y = 3 is
The non zero value of ‘a’ for which the lines 2x – y + 3z + 4 = 0 = ax + y – z + 2 and x – 3y + z = 0 = x + 2y + z + 1 are co-planar is
If the lines 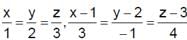 and
and 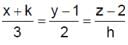 are concurrent then
are concurrent then
The coplanar points A, B, C, D are (2 – x, 2, 2), (2, 2 – y, 2), (2, 2, 2 – z) and (1, 1, 1) respectively. Then
The direction ratios of a normal to the plane through (1, 0, 0), (0, 1, 0), which makes an angle of π/4 with the plane x + y = 3 are
Let the points A(a, b, c) and B(a', b', c') be at distances r and r' from origin. The line AB passes through origin when
Let L be the line of intersection of the planes 2x + 3y + z = 1 and x + 3y + 2z = 2. If L makes an angle ? with the positive x-axis, the cos α equals
If a line makes an angle of π/4 with the positive directions of each of x-axis and y-axis, then the angle that the line makes with the positive direction of the z-axis is
If the angle θ between the line 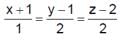 and the plane
and the plane 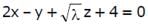 is such that sinθ = 1/3 The value of λ is
is such that sinθ = 1/3 The value of λ is
A line makes the same angle θ with each of the x and z-axis. If the angle θ, which it makes with y-axis is such that sin2 β = 3 sin2 θ, then cos2θ equals
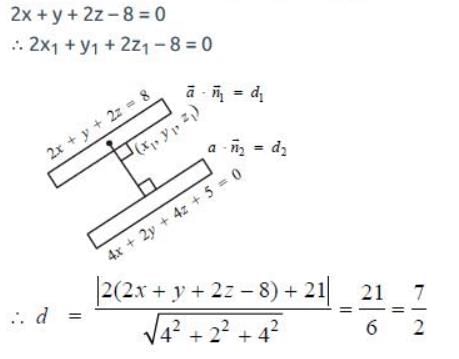
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the points of intersection are given by
The lines 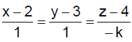 and
and 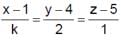 are coplanar if
are coplanar if
The equation of plane which meet the co-ordinate axes whose centroid is (a, b, c)



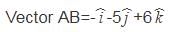
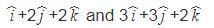
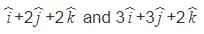 is normal to the required plane
is normal to the required plane