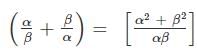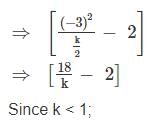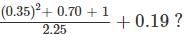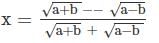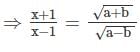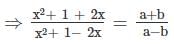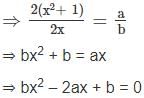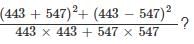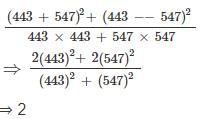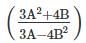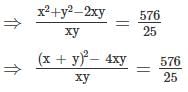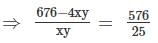CDS I - Mathematics Previous Year Question Paper 2017 - CDS MCQ
30 Questions MCQ Test - CDS I - Mathematics Previous Year Question Paper 2017
(x + 4) is a factor of which one of the following expressions?
If α and β are the roots of the quadratic equation 2x2 + 6x + k = 0, where k < 0, then what is the maximum value of (α/β + β/α)?
Consider the following sentences:
1. If a = bc with HCF(b, c) = 1, then HCF(c, bd) = HCF(c, d).
2. If a = bc with HCF(b, c) = 1, then LCM(a, d) = LCM(c, bd).
Q. Which of the above statements is/are correct?
What is the number of digits in 240? (Given that log102 = 0.301)
If one root of (a2 – 5a + 3)x2 + (3a – 1)x + 2 = 0 is twice the other, then what is the value of ‘a’?
What is the remainder when the number (4444)4444 is divided by 9?
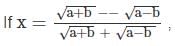 then what is bx2 – 2ax + b equal to (b ≠ 0)?
then what is bx2 – 2ax + b equal to (b ≠ 0)?
If x = t 1/(t – 1) and y = t t/(t – 1), t > 0, t ≠ 1 then what is the relation of x and y?
If A : B = 3 : 4, then what is the value of the expression 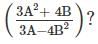
If A = {x : x is a multiple of 7},
B = {x : x is a multiple of 5} and
C = {x : x is a multiple of 35}
Q. Then which of the following is null set?
If x = 2 + 22/3 + 21/3, then what is the value of x3 – 6x2 + 6x?
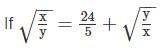 and x + y = 26, then what is the value of xy?
and x + y = 26, then what is the value of xy?
What is the solution of the equation x log10(10/3) + log103 = log10(2 + 3x) + x?
If α and β are the roots of the equation x2 + px + q = 0, then what is α2 + β2 equal to?
If a3 = 335 + b3 and a = 5 + b, then what is the value of a + b (given that a > 0 and b > 0)?
If 9x 3y = 2187 and 23x 22y – 4xy = 0, then what can be the value of (x + y)?
The pair of linear equations kx + 3y + 1 = 0 and 2x + y + 3 = 0 intersect each other, if
The number of prime numbers which are less than 100 is
The cost of diamond varies directly as the square of its weight. A diamond broke into four pieces with their weights in the ratio of 1 ∶ 2 ∶ 3 ∶ 4. If the loss in total value of the diamond was Rs. 70000, what was the price of the original diamond?
In a 100 m race, A runs at a speed of 5/3 m/s. If A gives a start of 4 m to B and still beats him by 12 seconds, what is the speed of B?
If 15 men take 21 days of 8 hours each to do a piece of work, then what is the number of days of 6 hours each that 21 women would take, if 3 women would as much work as 2 men?
What number must be subtracted from both the numerator and denominator of the fraction 27/35 so that it becomes 2/3?
The mean of 5 numbers is 15. If one more number is included, the mean of 6 numbers becomes 17. What is the included number?
The mean marks obtained by 300 students in a subject are 60. The mean of top 100 students was found to be 80 and the mean of last 100 students was found to be 50. The mean marks of the remaining 100 students are
Consider the following distribution

Q. If the mean of the above distribution is 50 then what is the value of f?
In a pie diagram, there are four slices with angles 150°, 90°, 60° and 60°. A new pie diagram is formed by deleting one of the slices having angle 60° in the given pie diagram. In the new pie diagram
In an asymmetrical distribution, if the mean and median of the distribution are 270 and 220 respectively, then the mode of the data is