JEE Advanced Level Test: Continuity and Differentiability- 3 - JEE MCQ
13 Questions MCQ Test - JEE Advanced Level Test: Continuity and Differentiability- 3
The number of points at which the function f(x) = max. {a – x, a + x, b} – ∞ < x < ∞, 0 < a < b cannot be differentiable is
The function f(x) is defined by f(x) = 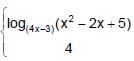
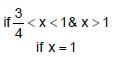
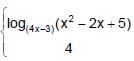
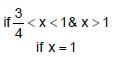
A point where function f(x) is not continuous where f(x) = [sin [x]] in (0, 2π) ; is ([ * ] denotes greatest integer ≤ x)
Let f(x) = [n + p sin x], x ∈ (0, π), n ∈ I and p is a prime number. Then number of points where f(x) is not differentiable is (where [ * ] denotes greatest integer function)
If f is a real-valued differentiable function satisfying |f(x) – f(y)| ≤ (x – y)2, x, y ∈ R and f(0) = 0, then f(1) equals
If f(x) = 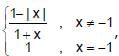 , then f([2x]) is (where [ * ] represent greatest integer function)
, then f([2x]) is (where [ * ] represent greatest integer function)
The value of f(0), so that the function, f(x)= becomes continuous for all x, is given by
becomes continuous for all x, is given by
If f(x) = 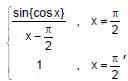 then f(x) is (where { * } represents the fractional part function)
then f(x) is (where { * } represents the fractional part function)
In order that function f (x) = (x + 1)cot x is continuous at x = 0, f (0) must be defined as
f is a continuous function on the real line. Given that x2 + (f(x) – 2) x – . f(x) + 2
– 3 = 0. then the value of f(
)
Given f(x)=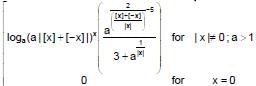 then (where [*] represent the integral part function)
then (where [*] represent the integral part function)


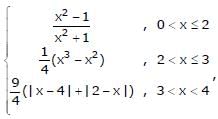 , then
, then
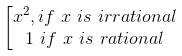 then
then











