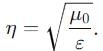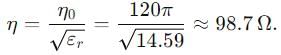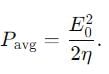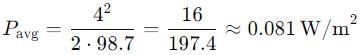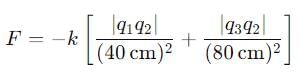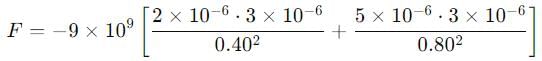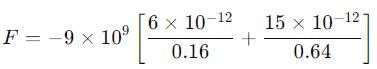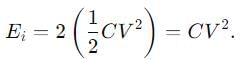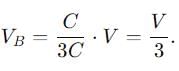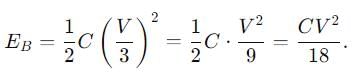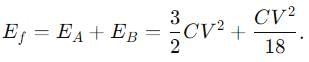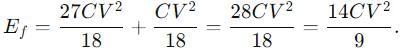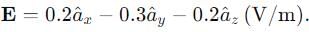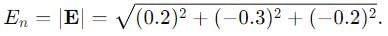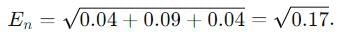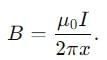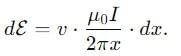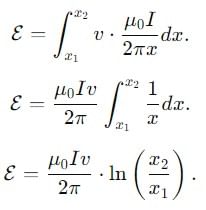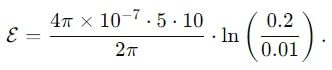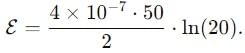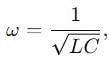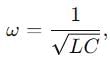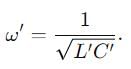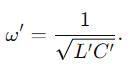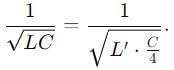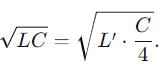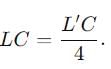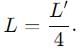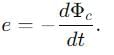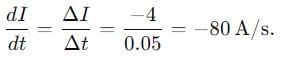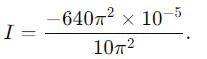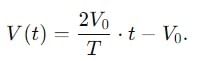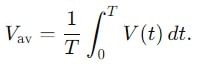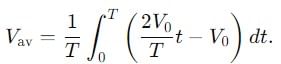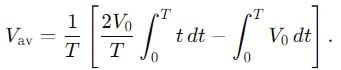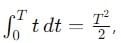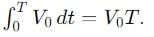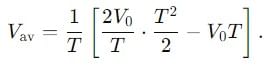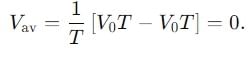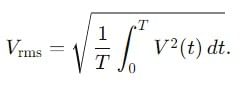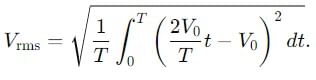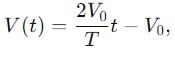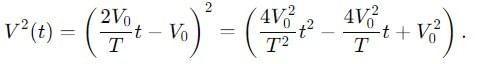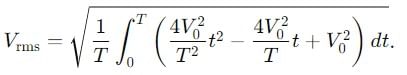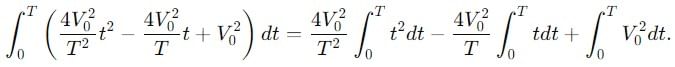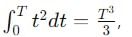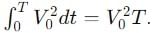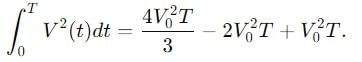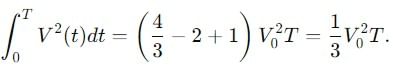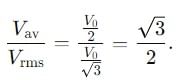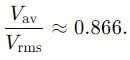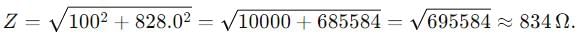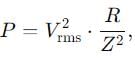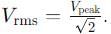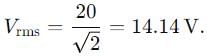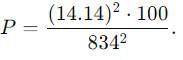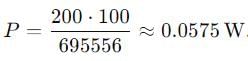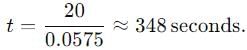IIT JAM Physics MCQ Test 5 - Physics MCQ
30 Questions MCQ Test - IIT JAM Physics MCQ Test 5
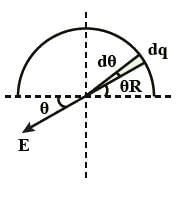
What is the electric field at the center of a uniformly charged semicircular arc i.e., at point P in Fig.

Two electric dipoles p1 and p2 are placed at (0, 0, 0) and (2, 0, 0) respectively with both of them pointing in the +z direction. Without changing the orientations of the dipoles. P2 is moved to (0. 4. 0). The ratio of the electrostatic potential energy of the dipoles after moving to that before moving is.
A spherical piece of radius much less than the radius of a charged spherical shell (charge density σ) is removed from the shell itself then electric field intensity at the mid point of aperture is


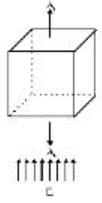
A cubical box sits in a uniform electric field as shown in Fig. What is the net flux coming out of the box.
A charge q is placed at the centre of the line joining two equal charges O. The system of three charges will be in equilibrium if q equal to
A total charge Q is broken in two parts Q1 and Q2 and they are placed at a distance Rfrom each other. The maximum force of repulsion between them will occur, when
Does the potential function φ = q(x2 + y2 + z2)-1/2 satisfies the laplace’s equations.
If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
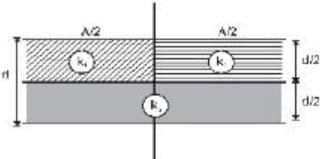
Two slabs of the same dimensions, having dielectric constants K1 and K2. completely fill die space between the plates of a parallel plate capacitor as shown in the figure. If C is the original capacitance of the capacitor, the new capacitance is
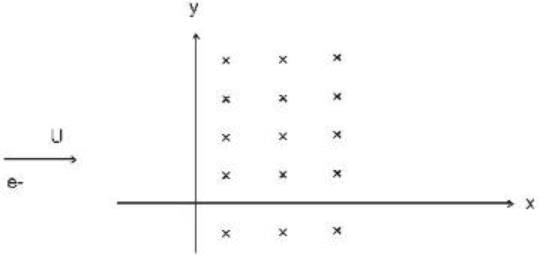
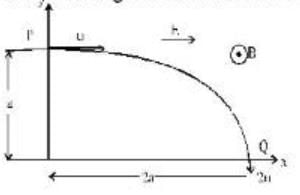
An electron moving with a speed 'u‘ along the position x - axis at y = 0 enters a region of uniform magnetic field 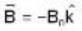 which exists to the right of y - axis . The electron exists from the region after sometimes with the speed V at coordinate y then
which exists to the right of y - axis . The electron exists from the region after sometimes with the speed V at coordinate y then
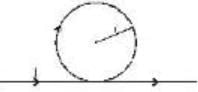
A long straight conductor, carrying a current L is bent into the shape shown in the figure. The radius of the circular loop is r. The magnetic field at the centre of the loop is
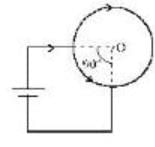
A battery of emf V volt is connected across a coil of uniform wire as shown. The radius of the coil is 'a' metres and the total resistance of the coil is R ohm. The magnetic field at the centre O of the coil (in tesla) is
In terms of basic units of mass (M). Length (L). time (Tr and charge 0. the dimensions of magnetized field (H» are
A magnetic needle is kept in a non-uniform magnetic field. It experiences:-
A particle of charge +q and mass m moving under the influence of a uniform electric field Ei and a uniform magnetic field B k follows a trajectory from P to Q as shown in the figure. The velocities at P and Q are 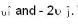 Which of the following statement is correct?
Which of the following statement is correct?
A series LCR circuit containing a resistance of 120 Ω has angular lesonance frequency 4 × 105 rad s-1. At resonance the voltages across resistance and inductance are 60 V and 40 V respectively.
A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin 0. A negatively charged particle P is released from rest at the point (0. 0. Z0) where Z0 > 0. Then the motion of P is :
Three point charges are placed at the following points on the x axis: + 2μC at x = 0, - 3μC at x = 40 cm. - 5μC at x = 120 cm. What is the force (in Newton) on the - 3μC charge ?
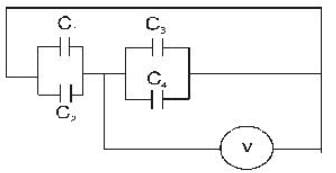
Four capacitors, each of 25μF.are connected as shown in the following circuit. A d.c. voltmeter reads 200 volts. The charge (in coulomb) on each capacitor is _____
The figure shows two identical parallel plate capacitors connected to a battery with switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of constant 3. The ratio of the total energy stored in both capacitors before and after tire introduction of the dielectric is ____

The electric field intensity at a point on line surface of a conductor is given by 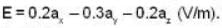 What is the surface charge density (in Pc/m2) at the point.
What is the surface charge density (in Pc/m2) at the point.
A copper rod of length 0.19 m is moving with uniform velocity 10 ms-1 parallel to a long straight wire carrying a current of 5A. The rod is perpendicular to the wire with its ends at distance 0.01 m and 0.2 m from it. Calculate the e.m.f. induced 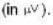
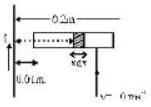
In an LCR circuit, the capacitance is made one - fourth when in resonance, then how many times the inductance should be changed, so that the circuit remains in resonance?
A 50 Hz A.C. current of peak value 1A flows through the primary coil of a transformer. If the mutual inductance between primary and secondary is 1.5 H. the mean value of the induced voltage (in V) is ________ .
A long solenoid of diameter 0.1 m has 2 * 104 turns per meter. At the centre of, the solenoid a 100 turn coil of radius 0.01m is placed with its axis coinciding with that of the solenoid. The current in the solenoid is decreasing at a constant rate from +2A to -2A in 0.05 sec. Find the total charge (in μC ) flowing through the coil during this time if the resistance of the coil is 10 π2 ohm.
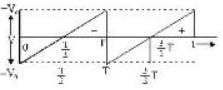
Find the ratio of average and rms value for the saw-tooth voltage of peak value V0 as shown in Fig.
A 750 hertz, 20 V source is connected to a resistance of 100 ohm. an inductance of 0.1803 henry and a capacitance of 10 microfarad all in series. Calculate the time (in sec .) in which the resistance (thermal capacity 2J/oC ) will get heated by 10oC.
A long solid non-conducting cylinder of radius R is charged such that the volume charge density is proportional to r where r is the distance from axis. The electric field E at a distance r(r<R) will depend on r as


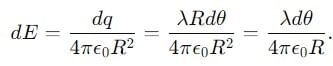
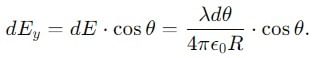
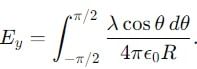
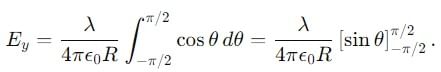

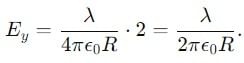
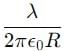
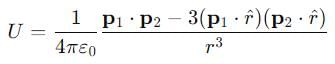
 is the unit vector along the line joining the two dipoles, and r is the distance between them.
is the unit vector along the line joining the two dipoles, and r is the distance between them.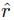 = 0 (no component of p1 along
= 0 (no component of p1 along  ).
).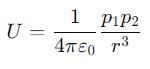
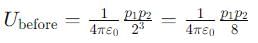
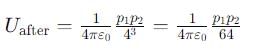


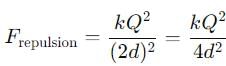
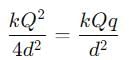
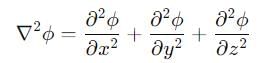
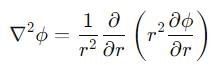

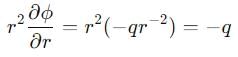
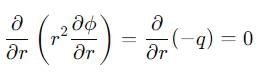
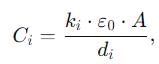
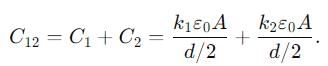
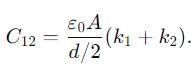
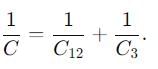
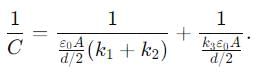
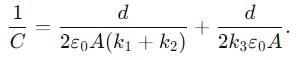
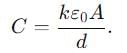

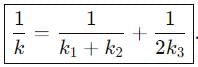
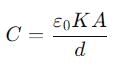
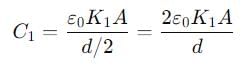
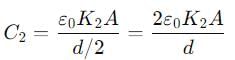
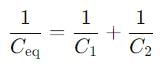
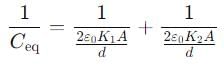
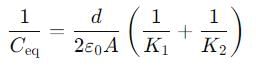
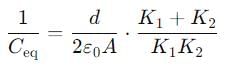
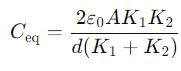

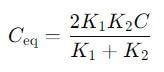
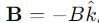 , pointing into the page (negative z-direction).
, pointing into the page (negative z-direction).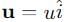 along the x-axis.
along the x-axis.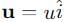 and
and  :
: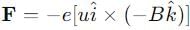
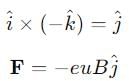
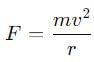
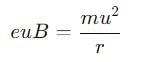
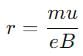
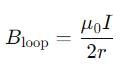
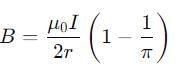
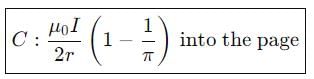
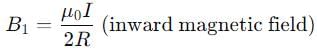
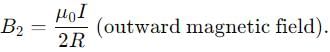
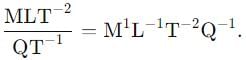
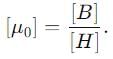
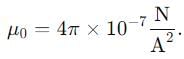
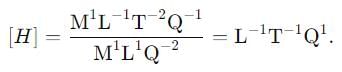
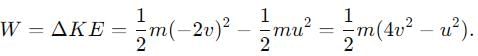
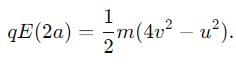
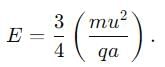
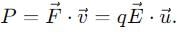
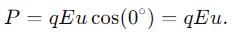

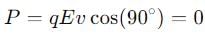
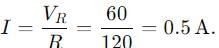
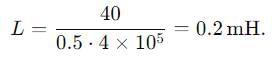
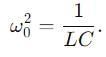

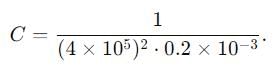
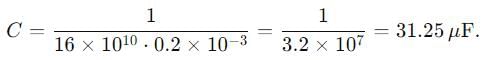
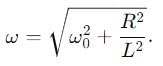
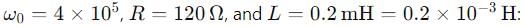
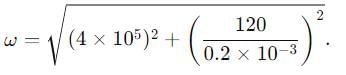
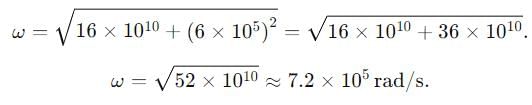
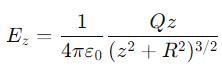
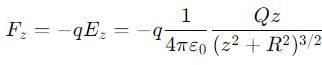
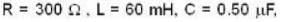
 Then
Then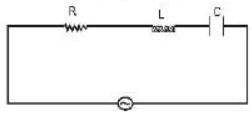
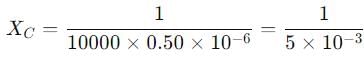
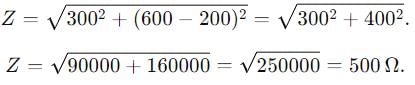
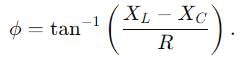

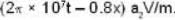 Then,
Then,