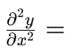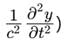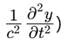Application Of Schrodinger Wave Equation – MSQ - Physics MCQ
10 Questions MCQ Test - Application Of Schrodinger Wave Equation – MSQ
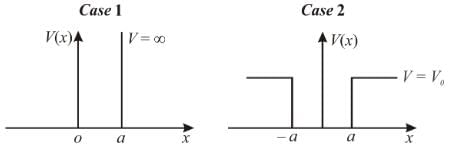
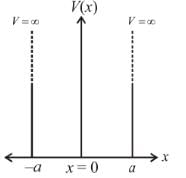
Consider two cases of one dimensional potential well. The first case is an infinite potential will V = 0, for a < x < 0 the second case is a finite potential well. Which of the following is true? [for E < V0]

The Steady-state form of Schrodinger wave equation is _____________
For a wave function ψ(x) , its time dependence can be seen from 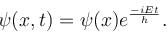 Select the correct option.
Select the correct option.
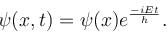 Select the correct option.
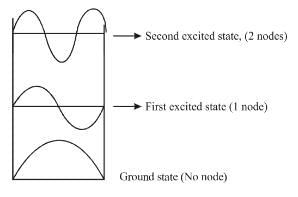
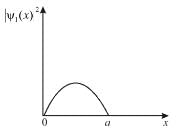
Select the correct option.Consider the solutions to particle in one dimensional box of length, L.
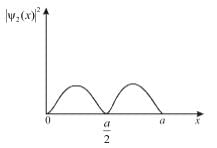
Which of the following is true for the group of functions ψ2(x)
Choose the correct option.
For the case of particle in a one dimensional box.
For the above cases of one-dimensional infinite and finite potential wells which of the following is true?
For a particle in a one dimensional box,
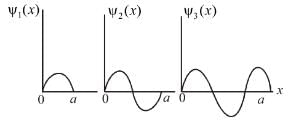
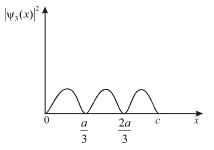
There is zero probability of finding the particle at
Which of the following is true in case of a free particle?
Which of the following is true for a quantum harmonic oscillator?
Which of the following can be the solution of Schrondinger's equation?


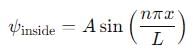
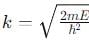 , and E < V0.
, and E < V0.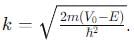
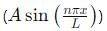 and inside the finite well (Bcos(kx)).
and inside the finite well (Bcos(kx)).
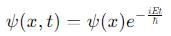
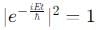 . Similarly,
. Similarly,  , which also has no time dependence. Thus, this option is correct.
, which also has no time dependence. Thus, this option is correct.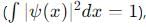 then the time-dependent wavefunction ψ(x, t) remains normalized because the time-dependent factor e−iEt/h does not affect the normalization
then the time-dependent wavefunction ψ(x, t) remains normalized because the time-dependent factor e−iEt/h does not affect the normalization 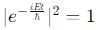 . Thus, this option is correct.
. Thus, this option is correct.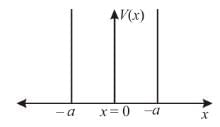
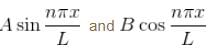
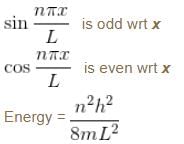
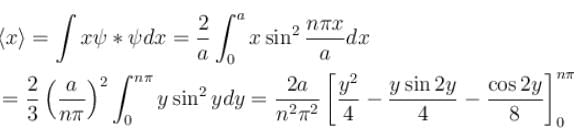
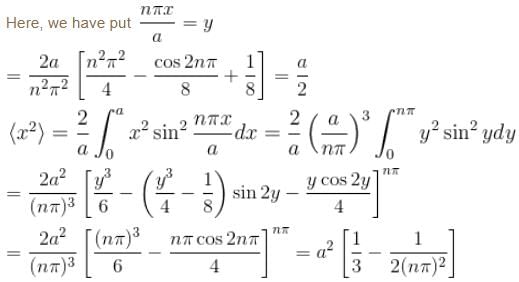
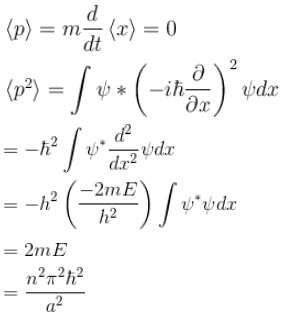
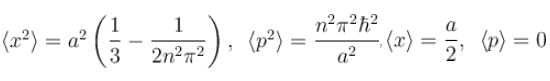
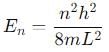
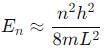
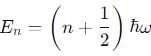
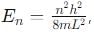 , especially for deep finite wells.
, especially for deep finite wells.
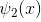
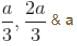
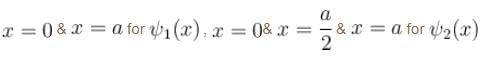
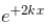
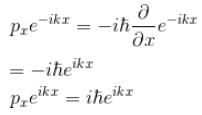
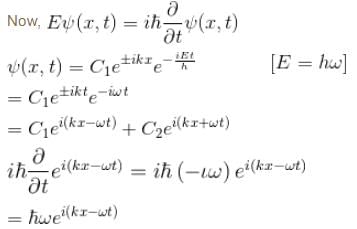
 (linear combination of the two), The solutions of the Schrodinger equation are both energy and momentum eigenfunctions
(linear combination of the two), The solutions of the Schrodinger equation are both energy and momentum eigenfunctions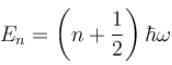 for a harmonic oscillator
for a harmonic oscillator