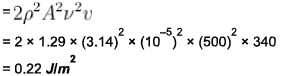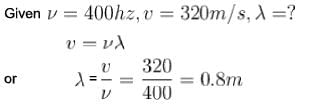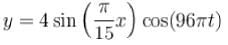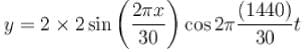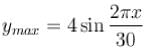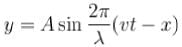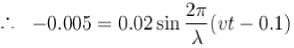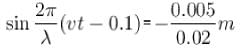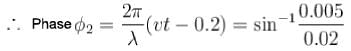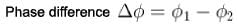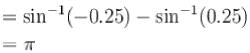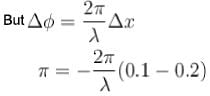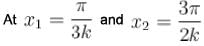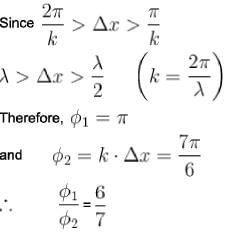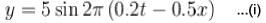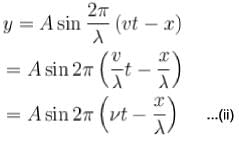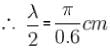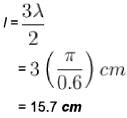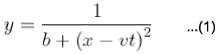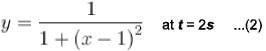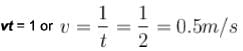All Courses
Get the App Signup / Login
Sign in Open App
IIT JAM Exam  >  IIT JAM Tests  >  Waves NAT Level - 1 - IIT JAM MCQ

Waves NAT Level - 1 - IIT JAM MCQ


Test Description

10 Questions MCQ Test - Waves NAT Level - 1

Waves NAT Level - 1 for IIT JAM 2024 is part of IIT JAM preparation. The Waves NAT Level - 1 questions and answers have been prepared according to the IIT JAM exam syllabus.The Waves NAT Level - 1 MCQs are made for IIT JAM 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Waves NAT Level - 1 below.
Solutions of Waves NAT Level - 1 questions in English are available as part of our course for IIT JAM & Waves NAT Level - 1 solutions in Hindi for IIT JAM course. Download more important topics, notes, lectures and mock test series for IIT JAM Exam by signing up for free. Attempt Waves NAT Level - 1 | 10 questions in 30 minutes | Mock test for IIT JAM preparation | Free important questions MCQ to study for IIT JAM Exam | Download free PDF with solutions
*Answer can only contain numeric values
Waves NAT Level - 1 - Question 1
Save

Plane harmonic waves of frequency 500 Hz are produced in air with displacement amplitude 1 x 10-3 cm. Deduce energy flux in J/m2) in the wave (density of air =1.29 gm/lit, speed of sound in air = 340 m/s).


Detailed Solution for Waves NAT Level - 1 - Question 1


The correct answer is: 0.22

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 2
Save

Plane harmonic waves of frequency 500 Hz are produced in air with displacement amplitude 1 x 10-3 cm.  Deduce pressure amplitude (in N/m2).  (density of air = 1.29 gm/lit, speed of sound in air = 340m/s)


Detailed Solution for Waves NAT Level - 1 - Question 2

Given A = 1 x 10-3 cm = 10-5 m, v = 500 Hz, v = 340 m/s, p = 1.29 g/lit = 1.29 kg/m3
Pressure amplitude

= 2 x 3.14 x 10-5 x 500 x 340 x 1.29
= 13.8 N/m2 
The correct answer is: 13.8

1 Crore+ students have signed up on EduRev. Have you? Download the App
*Answer can only contain numeric values
Waves NAT Level - 1 - Question 3
Save

If the frequency of a tuning fork is 400 Hz and the velocity of sound in air is 320 m/s, find how far does the sound travel (in m) while the fork completes 30 vibrations?


Detailed Solution for Waves NAT Level - 1 - Question 3


∴ Distance travelled by the wave when the fork completes 1 vibration = 0.8 m.
So distance travelled by the wave when the fork completes 30 vibrations.
= 0.8 x 30
= 24m
The correct answer is: 24

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 4
Save

The vibrations of a string of length 60 cm fixed at both ends are represented by the equation

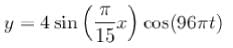
where x and y are in cm and t in seconds. What is the maximum displacement of point x = 5cm ?

Detailed Solution for Waves NAT Level - 1 - Question 4

The given equation is :

This can be written as :

This shows that a = 2 cm, λ =30 cm and ω = 1440 cm/s
The maximum displacement is given by :

For x = 5 cm

The correct answer is: 3.464

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 5
Save

A transverse harmonic wave of amplitude 0.02 m is generated at one end (x = 0) along horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time, the displacement of the particle at x = 0.1 m is 0.005 m and that of the particle at x = 0.2 m is 0.005 m. Calculate the wavelength of the wave?

Detailed Solution for Waves NAT Level - 1 - Question 5

The general equation of this wave is given by

Here A = 0.02 m
Again, when x = 0.1m, y = -0.005 m

or


Again x = 0.2m, y = 0.005m





or λ = 0.2m
The correct answer is: 0.2

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 6
Save

Equations of a stationary and a travelling waves are as follows :

The phase difference between two points 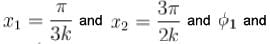 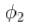respectively for the two waves. The ratio  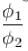is :

Detailed Solution for Waves NAT Level - 1 - Question 6


sin kx1, or sin kx2 is not zero.
Therefore, neither of x1 or x2 is a node


The correct answer is: 0.857

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 7
Save

A simple harmonic wave travelling x-axis is given by y = 5 sin 2π ( 0.2t - 0.5x) [x is in m and t in s]. Calculate the amplitude (in m ).

Detailed Solution for Waves NAT Level - 1 - Question 7

Here
But the standard progressive wave equation is :

Comparing equation (i) and (ii), we have

A = 5cm

The correct answer is: 5/100 

= 0.05m

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 8
Save

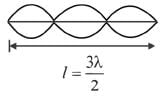
The equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by :
 The length of the string is :

Detailed Solution for Waves NAT Level - 1 - Question 8


Wave number


or

The correct answer is: 15.7

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 9
Save

A wave of frequency 400 Hz is travelling with a velocity 800 m/s. How far are two points situated whose displacement differs in phase by  ?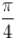

Detailed Solution for Waves NAT Level - 1 - Question 9

*Answer can only contain numeric values
Waves NAT Level - 1 - Question 10
Save

The amplitude of wave disturbance propagating in positive x-axis is given by 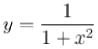 at t = 0 and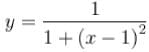at t= 2s, where x and y are in meters. The shape of the disturbance does not change during the propagation. The velocity (in m/s) of the wave is :

Detailed Solution for Waves NAT Level - 1 - Question 10

The given pulse is of the form

where v is the wave velocity 
Given equation is

Comparing eq. (1) and (2), we get

The correct answer is: 0.5

Information about Waves NAT Level - 1 Page
In this test you can find the Exam questions for Waves NAT Level - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Waves NAT Level - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Waves NAT Level - 1

Find all the important questions for Waves NAT Level - 1 at EduRev.Get fully prepared for Waves NAT Level - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Waves NAT Level - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Waves NAT Level - 1 resources.

Waves NAT Level - 1 MCQs with Answers

Prepare for the Waves NAT Level - 1 within the IIT JAM exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Waves NAT Level - 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Waves NAT Level - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup