Math - 2018 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test - Math - 2018 Past Year Paper
Let 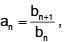 where b1 = 1, b2 = 1 and bn+2 = bn + bn+1,
where b1 = 1, b2 = 1 and bn+2 = bn + bn+1, 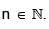 Then
Then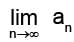 is:
is:
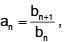 where b1 = 1, b2 = 1 and bn+2 = bn + bn+1,
where b1 = 1, b2 = 1 and bn+2 = bn + bn+1, 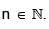 Then
Then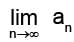 is:
is:If {v1, v2, v3} is a linearly independent set of vectors in a vector space over 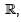 then which one of the following sets is also linearly independent?
then which one of the following sets is also linearly independent?
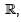 then which one of the following sets is also linearly independent?
then which one of the following sets is also linearly independent?Let a be a positive real number. If f is a continuous and even function defined on the interval [–a, a], then 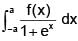 is equal to :
is equal to :
The tangent plane to the surface 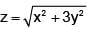 at (1, 1, 2) is given by
at (1, 1, 2) is given by
In 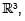 , the cosine of the acute angle between the surfaces x2 + y2 + z2 - 9 = 0 and z - x2 - y2 + 3 = 0 at the point (2, 1, 2) is :
, the cosine of the acute angle between the surfaces x2 + y2 + z2 - 9 = 0 and z - x2 - y2 + 3 = 0 at the point (2, 1, 2) is :
Let f :  be a scalar field,
be a scalar field, 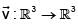 be a vector filed and let
be a vector filed and let 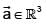 be a constant vector. If
be a constant vector. If 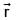 represents the position vector
represents the position vector 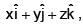 then which one of the following is FALSE?
then which one of the following is FALSE?
In 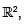 , the family of trajectories orthogonal to the family of asteroids x2/3 + y2/3 = a2/3 is given by
, the family of trajectories orthogonal to the family of asteroids x2/3 + y2/3 = a2/3 is given by
Consider the vector space V over 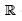 of polynomial functions of degree less then or equal to 3 defined on
of polynomial functions of degree less then or equal to 3 defined on 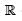 . Let T : V → V be defined by (Tf)(x) = f(x) – xf’(x). Then the rank of T is
. Let T : V → V be defined by (Tf)(x) = f(x) – xf’(x). Then the rank of T is
Let 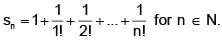 Then which one of the following is True for the sequence
Then which one of the following is True for the sequence 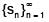 ?
?
Let a, b, c 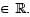 . Which of the following values of a, b, c do NOT result in the convergence of the series
. Which of the following values of a, b, c do NOT result in the convergence of the series

Let 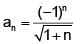 and let
and let 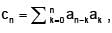 where
where 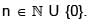 Then which one of the following is true?
Then which one of the following is true?
Suppose that f, g 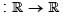 are differentiable functions such that f is strictly increasing and g is strictly decreasing. Define p(x) = f(g(x)) and q(x) = g(f(x)),
are differentiable functions such that f is strictly increasing and g is strictly decreasing. Define p(x) = f(g(x)) and q(x) = g(f(x)), 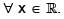 Then, for t > 0, the sign of
Then, for t > 0, the sign of 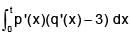 is :
is :
Let 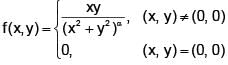 Then which one of the following is true for f at the point (0, 0)?
Then which one of the following is true for f at the point (0, 0)?
Let a, b 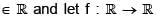 be a thrice differentiable function. If z = eu f(v), where u = ax + by and v = ax – by, then which one of the following is true?
be a thrice differentiable function. If z = eu f(v), where u = ax + by and v = ax – by, then which one of the following is true?
Consider the region D in the yz plane bounded by the line y = 1/2 and the curve y2 + z2 = 1, where y≥0. If the region D is revolved about the z- axis in 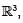 , then the volume of the resulting solid is :
, then the volume of the resulting solid is :
If 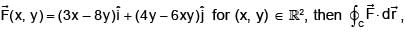 where C is the boundary of the triangular region bounded by the lines x = 0, y = 0 and x + y = 1 oriented in the anti- clockwise direction, is :
where C is the boundary of the triangular region bounded by the lines x = 0, y = 0 and x + y = 1 oriented in the anti- clockwise direction, is :
Let U, V and W be finite dimensional real vector spaces, T : U → V, S : V → W and P : W → U be linear transformations. If range (ST) = nullspace (P), nullspace (ST) = range (P) and rank (T) = rank (S), then which one of the following is true?
Let y(x) be the solution of the differential equation dy/dx + = , for x ≥ 0, y(0) = 0, where 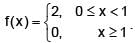 Then y(x) =
Then y(x) =
An integrating factor of the differential equation 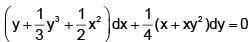 is:
is:
A particular integral of the differential equation 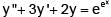 is:
is:
Let G be a group satisfying the property that f : 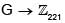 is a homomorphism implies f(g) = 0,
is a homomorphism implies f(g) = 0, 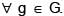 Then a possible group G is :
Then a possible group G is :
Let H be the quotient group 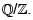 Consider the following statements.
Consider the following statements.
I. Every cyclic subgroup of H is finite.
II. Every finite cyclic group is isomorphic to a subgroup of H.
Which one of the following holds?
Let I denote the 4 × 4 identity matrix. If the roots of the characteristic polynomial of a 4 × 4 matrix M are 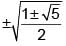 , then M8 =
, then M8 =
Consider the group 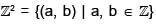 under component- wise addition. Then which of the following is a subgroup of
under component- wise addition. Then which of the following is a subgroup of 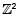 ?
?
Let f : 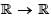 be a function and let J be a bounded open interval in
be a function and let J be a bounded open interval in 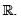 Define
Define
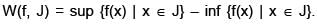
Which one of the following is false?



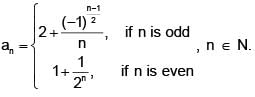
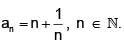 Then the sum of the series
Then the sum of the series 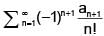 is:
is: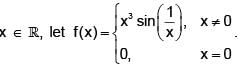 Then which one of the following is false?
Then which one of the following is false?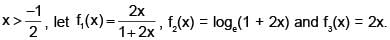 Then which one of the following is true?
Then which one of the following is true?










