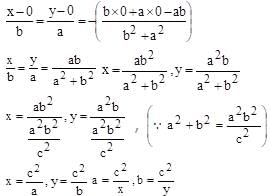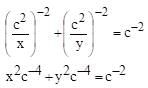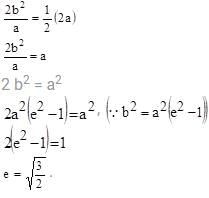JEE Main Practice Test- 4 - JEE MCQ
30 Questions MCQ Test - JEE Main Practice Test- 4
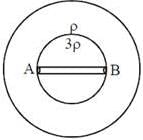
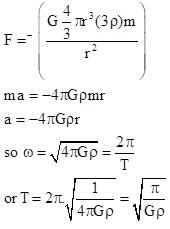
A planet of core density 3ρ and outer curst of density ρ has small tunnel in core. A small Particle of mass m is released from end A then time required to reach end B :

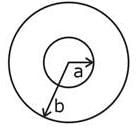
A small circular wire loop of radius a is located at the centre of a much larger circular wire loop of radius b as shown above (b> >a). Both loops are coaxial and coplanar. The larger loop carries a time (t) varying current I = I0 cos ωt where I0 and ω are constants. The large loop induces in the small loop an emf that is approximately equal to which of the following.

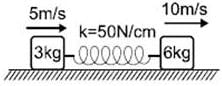
A spring mass system is placed on a frictionless horizontal surface as shown in the figure. The spring is expanded by 1/10m and the blocks are given velocities as shown, then maximum extension of spring is :

An electromagnetic wave of frequency f = 7.3MHz passes from a vacuum into a dielectric medium with permittivityε = 9. Then,
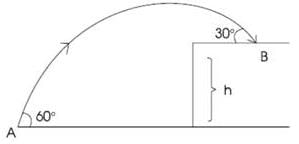
A particle is projected from point A towards a building of height h as shown at an angle of 60 ° with horizontal. It strikes the roof of building at B at an angle of 30 ° with the horizontal. The speed of projection is
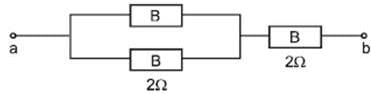
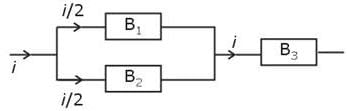
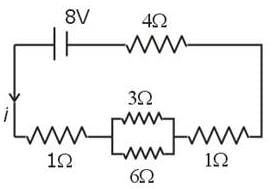
Three identical bulbs each of resistance 2Ω are connected as shown. The maximum power that can be consumed by individual bulb is 32W, then the maximum power consumed by the combination is :
A carrier wave has power of 1675 kW. If the side band power of a modulated wave subjected to 60%. Then find the amplitude modulation level
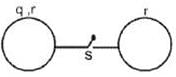
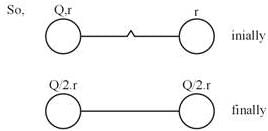
Two identical conducting spheres each having radius r are placed at large distance. lnitially charge on one sphere is q, while charge on another sphere is zero when they are connected by conducting wire as shown in figure then find total heat produced when switch S is closed :
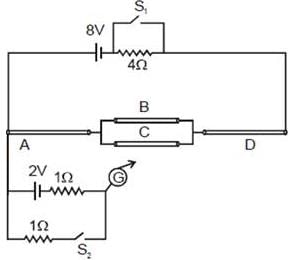
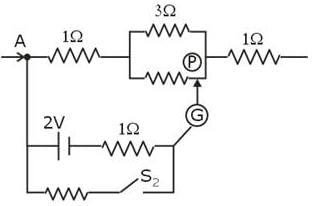
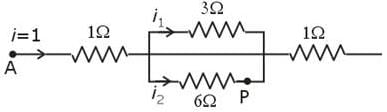
Four wire A, B, C and D each of length l = 10 cm and each of area of cross section is 0.1 m2 are connected in the given circuit. Then, the position of null point is
Given that resistivity
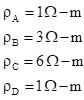
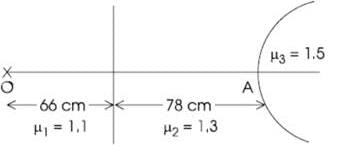
The radius of curvature of spherical surface is 10 cm. The spherical surface separates two media of refractive indices μ2 = 1.3 and μ3 = 1.5 as shown in Figure. The medium of refractive index 1.3 extends upto 78 cm from the spherical surface. A luminous point object O is at the distance of 144 cm from the spherical surface in the medium of refractive index μ1 = 1.1. The image formed by the spherical surface is at
A transformer has an efficiency of 80%. It is connected to a power input of 4 kW and 100 V. if the secondary voltage is 240 V, then the secondary current is
There are two balls in an urn whose colours are not known (each ball can be either white or black). A white ball is put into the urn. A ball is drawn from the urn. The probability that it is white is
The plane passing through the point (−2, −2, 2) and containing the line joining the points
(1, 1, 1) and (1, −1, 2) makes intercepts on the coordinates axes then sum of the lengths of intercepts is
If a, b, c are in GP and 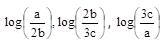 are in AP, then a, b, c are the lengths of the sides of a triangle which is
are in AP, then a, b, c are the lengths of the sides of a triangle which is
Sum of the series
1 + 3 + 6 + 10 + 15 + ……………………….n terms is
The solution of the equation (2x + y + 1) dx + (4x + 2y – 1) dy = 0 is
The area bounded by curves y = f(x), the x-axis and the ordinates x = 1 and x = b is (b - 1) sin (3b + 4). Then f(x) is-
If sin 5x + sin 3 x + sin x = 0, then the value of x other than zero, lying between 0 < x < π/2 is
The value of K, for which the equation (K–2)x2 + 8x + K + 4 = 0 has both the roots real distinct and negative is:
The equation of the common tangent touching the circle (x-3)2 + y2 = 9 and the parabola y2 = 4x above the x-axis, is
Let f(x) be a continuous function such that f(a – x) + f(x) = 0 for all x[0,a]. Then, the value of the integral 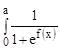 is equal to
is equal to
The circles which can be drawn to pass through (1,0) & (3,0) and touching the y-axis, intersect at an angle θ. The value of cos θ is equal to
a, b, c are positive numbers and abc2 has the greatest value 1/ 64. Then
If A and B are two square matrices such that B = –A–1 BA, then (A+B)2 is equal to
The set of all values of the parameter a for which the points of minimum of the function y = 1 + a2 x – x3
Satisfy the inequality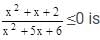
If for a variable line 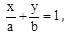 the condition a–2 + b–2 = c–2 (c is a constant), is satisfied, then the locus of foot of the perpendicular drawn from origin to this is:
the condition a–2 + b–2 = c–2 (c is a constant), is satisfied, then the locus of foot of the perpendicular drawn from origin to this is:
The eccentricity of the hyperbola whose latus rectum is half of its transverse axis, is


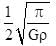
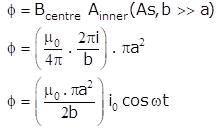
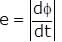
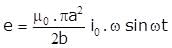

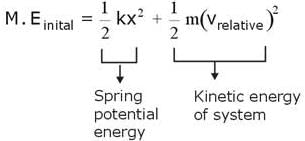
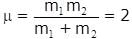 and vrelative =5 m/s
and vrelative =5 m/s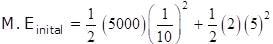
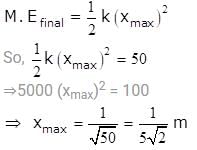
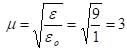
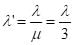
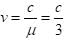
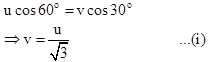
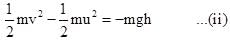
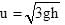
 Where PC is power of carrier wave, PS s sideband power and ‘m’ is modulation rate,
Where PC is power of carrier wave, PS s sideband power and ‘m’ is modulation rate,
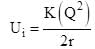 (Self energy of spherical conductor )
(Self energy of spherical conductor )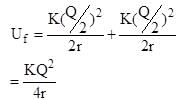
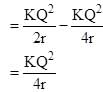
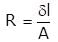
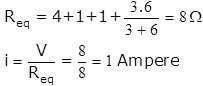
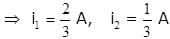
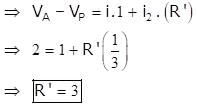
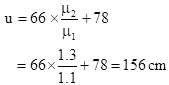
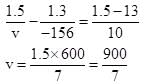
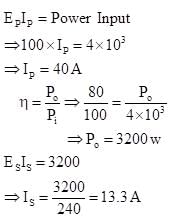
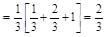

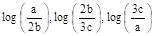 are in AP.
are in AP.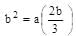 b = 2a/3 and c = 4a/9
b = 2a/3 and c = 4a/9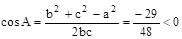
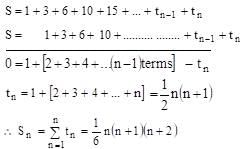
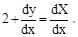 Therefore, the given equation is reduced to
Therefore, the given equation is reduced to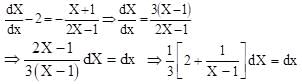
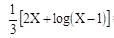 = x + constant
= x + constant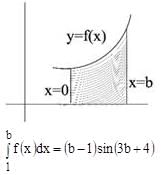
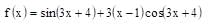
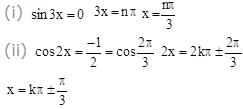
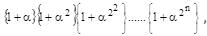 where
where 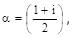 is equal to
is equal to 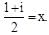 Hence the given series S is
Hence the given series S is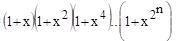

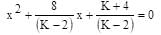
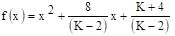
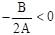
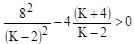
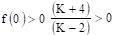

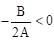
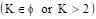
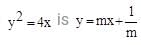
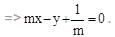
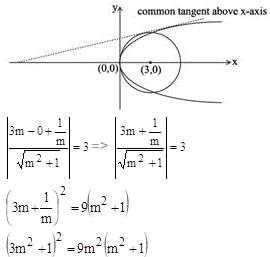
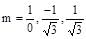
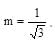 Hence equation of required common tangent is:
Hence equation of required common tangent is: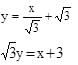
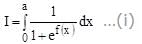
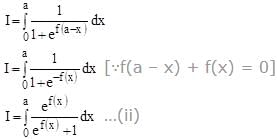
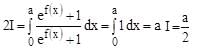
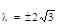
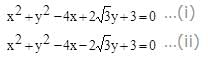
 respectively. Also the radii of each of the circles is r1 = r2 = 2
respectively. Also the radii of each of the circles is r1 = r2 = 2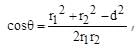 where d is the distance between their centers.
where d is the distance between their centers.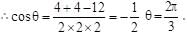

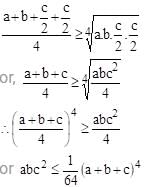
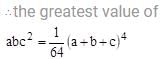
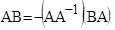
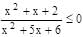 x2 + 5x + 6 < 0 –3 < x < –2
x2 + 5x + 6 < 0 –3 < x < –2 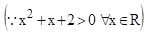
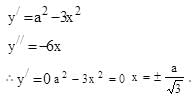
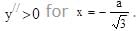 Hence y has minima at
Hence y has minima at 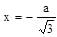 for a > 0.
for a > 0.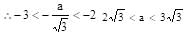
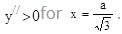 Hence y has minima at
Hence y has minima at 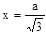 for a < 0.
for a < 0.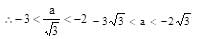
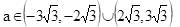
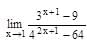 is
is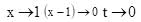
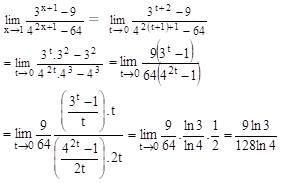
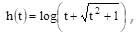 which is an odd function, therefore
which is an odd function, therefore 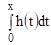 is even function.
is even function.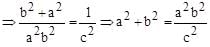
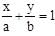 bx + ay – ab = 0
bx + ay – ab = 0