IIT JAM Physics Mock Test - 7 - Physics MCQ
30 Questions MCQ Test - IIT JAM Physics Mock Test - 7
A vessel of volume V = 30l contains ideal gas at temperature 00C. After a portion of the gas has been let out. the pressure in the vessel decreases by ΔP = 0.78 atm. Find the mass of the released gas. The gas density under the normal conditions is ρ = 1 .3 g/l. .
An ideal gas whose pressure varies with volume according to the following relation P = P0 - aV2. If we subject the gas to different pressures. What is the maximum temperature that the gas may attain?
A box containing 2 moles of a diatomic ideal gas at temperature T0 is connected to another identical box containing 2 moles of a monoatomic ideal gas at temperature 5T0. There are no thermal losses and the heat capacity of the boxes and vibrational degree of freedom are negligible. Find the final temp, of the mixture
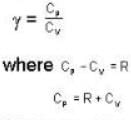
One mole of an ideal gas whose adiabatic exponent equals R undergoes a process in which the gas pressure relates to the temperature as P = aTα. The work performed by the gas if its temperature gets an increment ΔT.
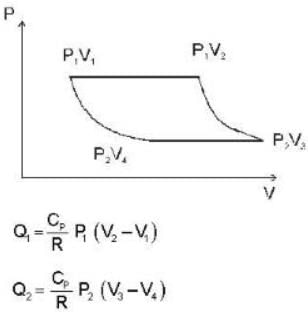
The efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes n times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to γ.
The heat required to convert 1 gm of water into steam under standard atm pressure if the entropy of water at the boiling point is 0.31 and for 100% steam at the steam temperature is 1.74 is:-
If y = x cos x is a solution of an nth order linear differential equation

With real constant coefficients, then the least possible value of n is:-
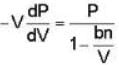
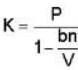
A monoatomic gas is described by the equation of state P(V - bn) = nRT Where b and R are constants and other quantities have their usual meanings. The maximum density (in makes per unit volume) to which this gas can be compressed is
Consider the surface corresponding to the equation
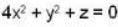
A possible unit tangent to this surface at the point (1.2.-8) is
An system at temperature T has three energy states 0, ± ε. The entropy of the system in the low temperature (T→0) and high temperature (T → ∝) limits are respectively,
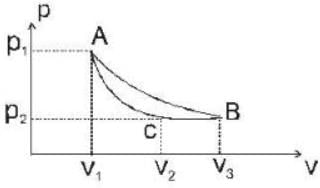
One mole of an ideal gas undergoes the cycle ACBA shown in the pV diagram below one of the curved lines in the cycle represents an isothermal change at temperature T, while the other represents and adiabatic change, the net heat gained by gas in this cycle is _____
An ideal gas at a temperature T is enclosed in a rigid container whose walls are initially at temperature T1, where T1 < T. The walls are covered on the outside with perfect thermal insulation and the system is allowed to come to equilibrium. The pressure exerted by the gas on the walls of the container.
Consider the CO molecule as a system of two point particles which has both translational and rotational degrees of freedom. Using classical statistical mechanics. the molar specific heat Cv of CO gas is given in form of the Boltzmann constant KB by
The vector 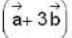 is perpendicular to
is perpendicular to  is perpendicular to
is perpendicular to 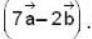 Then the angle between
Then the angle between 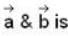
In the temperature range 100 - 1000 C. the molar specific heat of a metal varies with temperature T (measured in degrees Celsius) according to the formula  If 0.2 kg of the metal at 600 C is brought in thermal contact with 0.1 kg of the same metal at 300 c, the final equilibrium temperature in deg c, will be
If 0.2 kg of the metal at 600 C is brought in thermal contact with 0.1 kg of the same metal at 300 c, the final equilibrium temperature in deg c, will be
A monoatomic gas undergoes a process given by 2 du + 3dω = 0 Then the process is
An ideal gas in a Cylinder is Compressed adiabatic ally to one - third of its initial Volume. During this process 20 J work is done on the gas by compressing agent. Which of the following Statements is true for this case?
The ratio y = CP / CV of H2, gas is 7/5 at room temperature, and 5/3 at low temperatures (around 50 K). The reason for this change is
Calculate the variation of Cp with pressure at constant temperature of a substance for which the equation of state is given the relation
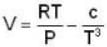
f(x) is a periodic function of x with a period of 2π. In the interval -π<x<π, f(x) is given by
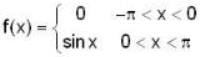
In the expansion of f(x) as a Fourier series of sine and cosine functions, the coefficient of cos 2x is
The volume of the portion of the cylinder x2 + y2 = 4 in the first octant between the lanes z = 0 and 3x - z = 0 is
For in isolated thermodynamical system, most probable, and root mean square values respectively of the molecular speeds of a gas room temperature being Maxwellian velocity distribution, then
For an isolated thermodynamical system P, V, T, U, S. and F represent the pressure. volume, temperature, internal energy, and free energy respectively. Then the following relation is true
The sublimation curve of solid ammonia is given by ln p = 23 - 3750/T and the vaporization curve of the liquid ammonia is given by In p = 19.5 -3050/T. where p is in mm of Hg and T is in K. The temperature of the triple point of ammonia is
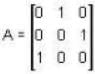
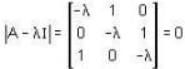
The eigen values of the matrix  are given by
are given by  Which one of the following statement is NOT true?
Which one of the following statement is NOT true?
Let  is a solution of the Laplace equation then the vector field
is a solution of the Laplace equation then the vector field  is
is



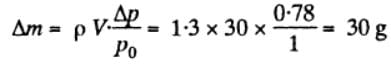
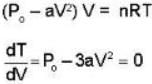
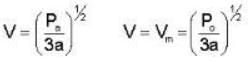
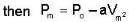
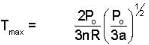

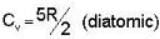


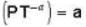


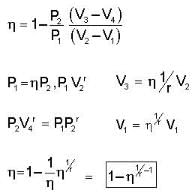
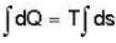
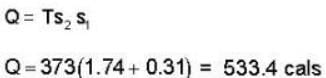

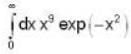
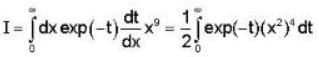
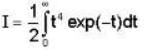
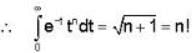
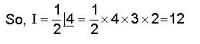
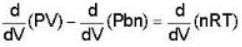
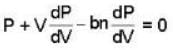
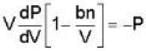
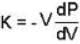
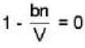
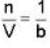
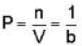
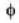 = 4x2 + y2 + z = 0
= 4x2 + y2 + z = 0 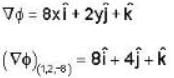
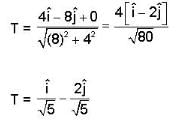

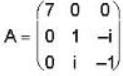
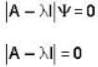
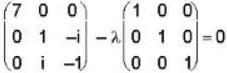

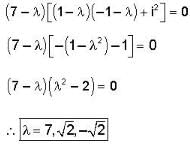
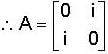
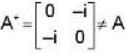
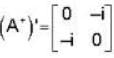

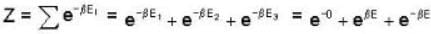
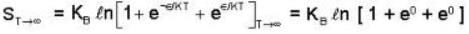
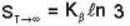
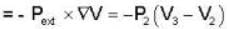
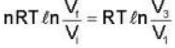
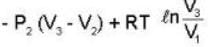
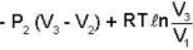
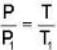
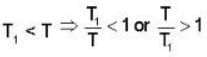
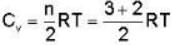
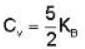
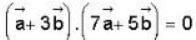
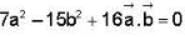 ..(i)
..(i)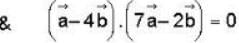
 ...(ii)
...(ii)
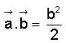
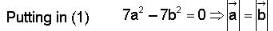
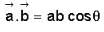
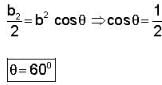
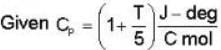
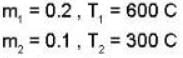
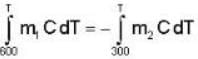
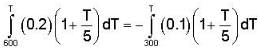
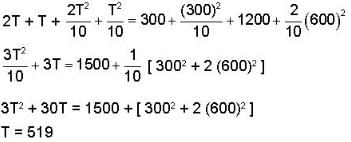
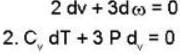
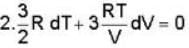
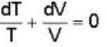
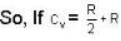
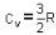

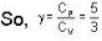
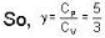
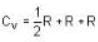
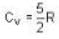
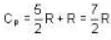
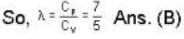
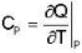
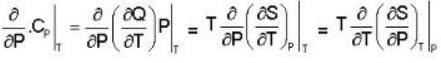
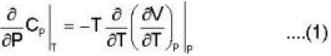
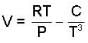
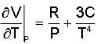
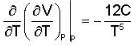 ...(ii)
...(ii)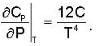
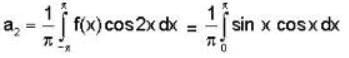
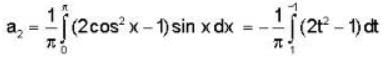 ( COS X = t )
( COS X = t )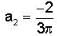
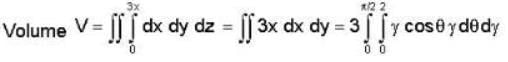
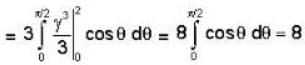

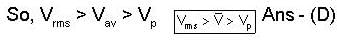
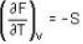
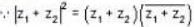
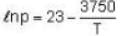 ...(i)
...(i)
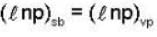
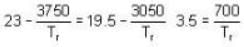
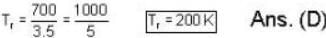
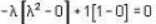
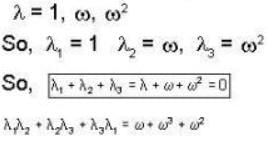
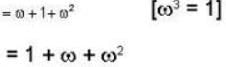
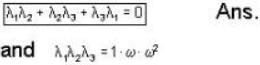
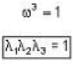
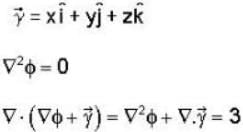
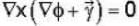
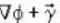 is not solenoidal but irrotational.
is not solenoidal but irrotational.











